243. 一个简单的整数问题2（树状数组）

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

输出样例：

4
55
9
15

 解析：

        一般树状数组都是单点修改、区间查询或者单点查询、区间修改。这道题都是区间操作。

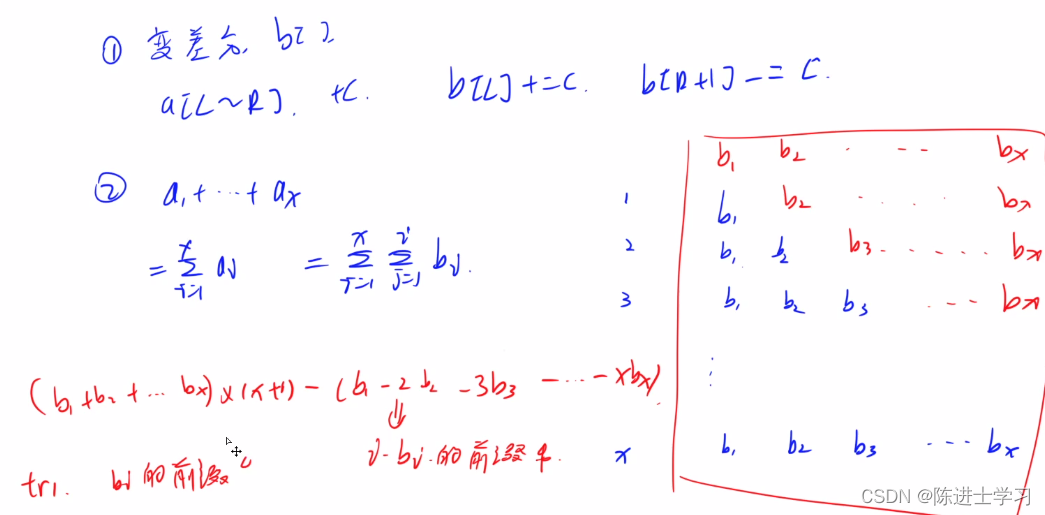
        1. 区间修改用数组数组维护差分数组

        2. 区间查询，需要log计算两个端点的前缀和。上图右侧，可以得出，计算前缀和需要维护差分序列和  i*b[ i ] 的差分序列。

文章来源地址https://uudwc.com/A/0r1dA

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
ll n,m,a[N],b[N],tr1[N],tr2[N];
int lowbit(int x){
	return x&-x;
}
void add1(int x,ll k){
	for(int i=x;i<=n;i+=lowbit(i)) tr1[i]+=k;
}
void add2(int x,ll k){
	for(int i=x;i<=n;i+=lowbit(i)) tr2[i]+=k;
}
ll sum(int x){
	ll ans=0;
	for(int i=x;i;i-=lowbit(i)) ans+=tr1[i];
	ans*=x+1;
	for(int i=x;i;i-=lowbit(i)) ans-=tr2[i];
	return ans;
}
int main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
		b[i]=a[i]-a[i-1];
		add1(i,b[i]);
		add2(i,i*b[i]);
	}
	while(m--){
		char op;
		cin>>op;
		if(op=='C'){
			int l,r,d;
			scanf("%lld%lld%lld",&l,&r,&d);
			add1(l,d);
			add1(r+1,-d);
			add2(l,d*l);
			add2(r+1,-d*(r+1));
		}
		else{
			int x,y;
			scanf("%lld%lld",&x,&y);
			printf("%lld\n",sum(y)-sum(x-1));
		}
	}
	return 0;
}