比赛链接,邀请码:2023qsb
A Zlz’s problem(Easy Version)
题目描述
This is the easy version of this problem. The only difference between the easy and hard versions is the constraints on n n n and m m m.
So I won’t even take a glance
I would rather do my math
High on some calculus
I can forget about my past
Rather do my math - Robin Gan
Zlz has a bent for mathematics. He once participated in a high school math competition and got the first prize. Even now, he spends a lot of time thinking about mathematical problems. After enjoying the song Rather do my math, Zlz felt more enthusiastic about mathematics. Zlz was playing a card game. There were n cards numbered
1
1
1 to
n
n
n. Each time he randomly selected m cards from these n cards. After that he took down the minimum number of the cards he selected and then put the cards back.
Suddenly, one mathematics problem occurred to him. He wanted to know the expectation of the number he took down. Could you please write a program to calculate the answer modulo
998244353
998244353
998244353.
输入描述:
Only one line contains two integers
n
,
m
n,m
n,m – the number of cards, the number of cards that Zlz will select.
It is guaranteed that for all test cases:
1
≤
n
≤
20
;
1
≤
m
≤
n
1\le n\le 20;1\le m\le n
1≤n≤20;1≤m≤n .
输出描述:
Output an integer representing the answer modulo 998244353 998244353 998244353 in one line.
示例1
输入
3 2
输出
332748119
示例2
输入
5 3
输出
499122178
计算从 1 ∼ n 1\sim n 1∼n 中选取 m m m 个数中最小值的期望可以分别考虑最小值为 1 ∼ n − m 1\sim n-m 1∼n−m 时对期望的贡献。
最小值为
i
i
i 则情况数为
(
n
−
i
m
−
1
)
\binom{n-i}{m-1}
(m−1n−i) ,对期望的贡献为
(
n
−
i
m
−
1
)
×
i
(
n
m
)
\frac{\binom{n-i}{m-1}\times i}{\binom{n}{m}}
(mn)(m−1n−i)×i ,因此最终答案为:
∑
i
=
1
n
−
m
+
1
(
n
−
i
m
−
1
)
×
i
(
n
m
)
\frac{\sum\limits_{i=1}^{n-m+1}\binom{n-i}{m-1}\times i}{\binom{n}{m}}
(mn)i=1∑n−m+1(m−1n−i)×i
时间复杂度为 O ( n ) O(n) O(n) 。
#include <bits/stdc++.h>
constexpr int N = 20;
constexpr int P = 998244353;
using i64 = long long;
// assume -P <= x < 2P
int norm(int x) {
if (x < 0) {
x += P;
}
if (x >= P) {
x -= P;
}
return x;
}
template<class T>
T power(T a, int b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x)) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(P - x));
}
Z inv() const {
assert(x != 0);
return power(*this, P - 2);
}
Z &operator*=(const Z &rhs) {
x = i64(x) * rhs.x % P;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
friend std::istream &operator>>(std::istream &is, Z &a) {
i64 v;
is >> v;
a = Z(v);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const Z &a) {
return os << a.val();
}
};
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, m;
std::cin >> n >> m;
std::vector<Z> fac(N + 1), invfac(N + 1);
fac[0] = 1;
for (int i = 1; i <= N; i++) {
fac[i] = fac[i - 1] * i;
}
invfac[N] = fac[N].inv();
for (int i = N; i > 0; i--) {
invfac[i - 1] = invfac[i] * i;
}
auto binom = [&](int n, int m) {
if (n < m || m < 0 || n < 0) {
return Z(0);
}
return fac[n] * invfac[m] * invfac[n - m];
};
Z ans;
for (int i = 0; i <= n - m; i++) {
ans += Z(i + 1) * binom(n - i - 1, m - 1);
}
ans /= binom(n, m);
std::cout << ans << "\n";
return 0;
}
B Tree Tree Tree
题目描述
HXT is a good student. He loves to clean the public health area on weekends.One day, while he was sweeping leaves, a question occurred to him.
HXT是个好学生。他喜欢在周末打扫公共卫生区。一天,当他扫落叶的时候,他突然想到一个问题。
In front of him was a tree, consisting of n vertices. The vertices are numbered from 1 1 1 to n n n. The distance between two points on the tree is the number of sides contained in the shortest path between two points.
在他面前是一棵由 n n n 个顶点组成的树。顶点的编号从 1 1 1 到 n n n 。树上两点之间的距离是两点之间最短路径所包含的边数。
HXT wants to know how many different pairs of points there are on the tree where the distance between the two points is exactly equal to k k k, which is a given number.
HXT 想知道树形上有多少对不同的点它们之间的距离正好等于 k k k ,这是一个给定的数。
Note: ( u , v ) (u, v) (u,v) and ( v , u ) (v, u) (v,u) are treated as the same point pair and the answer is calculated only once.
注意: ( u , v ) (u, v) (u,v) 和 ( v , u ) (v, u) (v,u) 被视为同一个点对,答案只计算一次。
输入描述:
The first line contains two integers, n n n and k ( 2 ≤ n ≤ 50000 ; 1 ≤ k ≤ 500 ) . k\ (2\le n\le 50000;1\le k\le 500) . k (2≤n≤50000;1≤k≤500).
第一行包含两个整数 n n n 和 k ( 2 ≤ n ≤ 50000 ; 1 ≤ k ≤ 500 ) k\ (2\le n\le 50000;1\le k\le 500) k (2≤n≤50000;1≤k≤500) 。
Next there are n − 1 n-1 n−1 lines, each with two integers a i , b i a_i,b_i ai,bi, indicating that there is an edge between the node a i a_i ai and b i b_i bi.
接下来是 n − 1 n-1 n−1 行,每一行有两个整数 a i , b i a_i,b_i ai,bi,表示在节点 a i a_i ai 和 b i b_i bi 之间有一条边。
输出描述:
Output an integer representing the number of point pairs that satisfy the condition.
输出一个整数,表示满足条件的点对的数量。
示例1
输入
5 2
1 2
2 3
3 4
2 5
输出
4
示例2
输入
5 3
1 2
2 3
3 4
4 5
输出
2
因为这里 n n n 和 k k k 都不大,因此直接暴力 dp 可以通过本题。
设
dp[x][i]
\text{dp[x][i]}
dp[x][i] 表示节点
x
x
x 的子树中距离节点
x
x
x 距离为
i
i
i 的节点个数,则有如下转移方程:
dp
[
x
]
[
i
]
=
∑
y
∈
son
(
x
)
dp
[
y
]
[
i
−
1
]
\text{dp}[x][i]=\sum_{y\in \text{son}(x)}\text{dp}[y][i-1]
dp[x][i]=y∈son(x)∑dp[y][i−1]
在 dp 的过程中统计答案即可。时间复杂度为 O ( n k ) O(nk) O(nk) 。
#include <bits/stdc++.h>
using i64 = long long;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, k;
std::cin >> n >> k;
std::vector<std::vector<int>> adj(n);
for (int i = 0; i < n - 1; i++) {
int u, v;
std::cin >> u >> v;
u--, v--;
adj[u].push_back(v);
adj[v].push_back(u);
}
i64 ans = 0;
std::vector dp(n, std::vector<int>(k + 1));
std::function<void(int, int)> dfs = [&](int x, int fa) {
dp[x][0] = 1;
for (auto y: adj[x]) {
if (y == fa)continue;
dfs(y, x);
for (int i = 1; i < k; i++) {
ans += i64(dp[x][i]) * dp[y][k - i - 1];
}
for (int i = 0; i < k; i++) {
dp[x][i + 1] += dp[y][i];
}
}
ans += dp[x][k];
};
dfs(0, -1);
std::cout << ans << "\n";
return 0;
}
按重心将树分割成若干个连通块,然后再在连通块中按此方法分割,共分割 O ( log n ) O(\log n) O(logn) 层。对于每层单独统计经过重心的长度为 k k k 的路径,复杂度为 O ( n log n ) O(n\log n) O(nlogn) 。
#include <bits/stdc++.h>
using i64 = long long;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, k;
std::cin >> n >> k;
std::vector<std::vector<int>> adj(n);
for (int i = 0; i < n - 1; i++) {
int u, v;
std::cin >> u >> v;
u--, v--;
adj[u].push_back(v);
adj[v].push_back(u);
}
std::vector<int> size(n), dep(n);
std::vector<bool> vis(n);
std::function<int(int, int, int)> get = [&](int x, int fa, int s) {
size[x] = 1;
int ms = 0, rs = s - 1;
for (auto y: adj[x]) {
if (y == fa || vis[y])continue;
int p = get(y, x, s);
if (p != -1) {
return p;
}
size[x] += size[y];
ms = std::max(ms, size[y]);
rs -= size[y];
}
return std::max(ms, rs) <= s / 2 ? x : -1;
};
std::vector<int> a, b, cnt(n);
std::function<void(int, int)> dfs = [&](int x, int fa) {
b.push_back(x);
size[x] = 1;
dep[x] = dep[fa] + 1;
for (auto y: adj[x]) {
if (y == fa || vis[y])continue;
dep[y] = dep[x] + 1;
dfs(y, x);
size[x] += size[y];
}
};
i64 ans = 0;
std::function<void(int, int)> solve = [&](int x, int s) {
x = get(x, -1, s);
vis[x] = true;
dep[x] = 0;
cnt[0] = 1;
for (auto y: adj[x]) {
if (vis[y])continue;
dfs(y, x);
for (auto u: b) {
if (k >= dep[u]) {
ans += cnt[k - dep[u]];
}
}
for (auto u: b) {
cnt[dep[u]]++;
a.push_back(u);
}
b.clear();
}
for (auto u: a) {
cnt[dep[u]] = 0;
}
a.clear();
for (auto y: adj[x]) {
if (!vis[y]) {
solve(y, size[y]);
}
}
};
solve(0, n);
std::cout << ans << "\n";
return 0;
}
C Lost stars
题目描述
And…God, tell us the reason youth is wasted on the young
It’s hunting season and the lambs are on the run
Searching for meaning
But are we all lost stars trying to light up the dark?
lost stars - Maroon 5
Just as Wild_pointer was listening to lost stars, academician Zhou sent a ICPC training problem for him. “I had AC this problem, foolish Wild_pointer come to solve it.” said academician Zhou ironically. Wild_pointer immediately wrote a brute force algorithm and submitted. Unfortunately he got TLE for he mistook the data scale.
It’s quite certain that his program is correct. What is needed is improvement of the time and space complexity of the algorithm. Wild_pointer is such a fool. But he is afraid of being laughed at by academician Zhou. As an excellent algorithm competition contestant, could you please help him?
正当 Wild_pointer 在听 lost stars 的时候,周院士给他发来一道 ICPC 训练题,并嘲讽他:我 AC 了这道题,辣鸡 Wild_pointer 快来做!Wild_pointer 一看题马上写了个暴力交上去,结果 TLE 了(他看错题面数据量了)。
他的代码肯定是对的,只是需要一些算法时空复杂度的优化。Wild_pointer 太笨了,但是又不想被周院士嘲笑,你作为一个优秀的算竞人,你能帮帮他吗?
Wild_pointer’s code was written in Python:
Wild_pointer的代码是用 Python 写的,代码如下:
n=int(input())
global g
g=0
fib=[0,1]
def Dfs(n,s,p):
global g
if n==0:
g=(g+s)%p
return
for i in range(1,n+1):
Dfs(n-i,s*fib[i]%p,p)
for i in range(2,n+1): fib.append(fib[i-1]+fib[i-2])
q=9614361054979589693
Dfs(n,1,q)
print(g)
Please write a program to ensure that he can get AC.
Note that for the same input, the answer output of your program must be consistent with Wild_pointer’s program output, and your program must meet the limitations of this problem.
请写一段程序确保 Wild_pointer 能 AC 。
注意,对于相同的输入,你的程序输出答案必须同 Wild_pointer 的输出一样,而且你的程序还需要满足本题的限制。
输入描述:
Only one line contains an integer n n n. ( 1 ≤ n ≤ 1 0 10000 ) (1\le n \le 10^{10000}) (1≤n≤1010000)
一行一个整数 n ( 1 ≤ n ≤ 1 0 10000 ) n\ (1\le n \le 10^{10000}) n (1≤n≤1010000)
输出描述:
Output an integer representing the answer in one line.
输出一行一个整数表示答案。
示例1
输入
3
输出
5
示例2
输入
2
输出
2
通过打表可以发现题目中的函数计算结果构成的数列
a
a
a 满足:
a
i
=
{
1
(
i
=
1
)
2
(
i
=
2
)
2
×
a
i
−
1
+
a
i
−
2
(
i
>
2
)
a_i =\left\{\begin{matrix} 1\ (i=1)\\ 2\ (i=2)\\ 2\times a_{i-1}+a_{i-2}\ (i>2) \end{matrix}\right.
ai=⎩
⎨
⎧1 (i=1)2 (i=2)2×ai−1+ai−2 (i>2)
具体证明如下:
根据代码可知
a
n
=
∑
i
=
1
n
fib
i
×
a
n
−
i
=
∑
i
=
0
n
−
1
fib
n
−
i
×
a
i
\begin{align*} a_{n}&=\sum_{i=1}^{n} \text{fib}_{i}\times a_{n-i}\\ &=\sum_{i=0}^{n-1} \text{fib}_{n-i}\times a_i \end{align*}
an=i=1∑nfibi×an−i=i=0∑n−1fibn−i×ai
因此有
a
n
−
a
n
−
1
=
(
∑
i
=
0
n
−
1
fib
n
−
i
×
a
i
)
−
(
∑
i
=
0
n
−
2
fib
n
−
i
−
1
×
a
i
)
=
a
n
−
1
×
fib
1
+
∑
i
=
0
n
−
2
(
fib
n
−
i
−
fib
n
−
i
−
1
)
×
a
i
=
a
n
−
1
+
∑
i
=
0
n
−
2
fib
n
−
i
−
2
×
a
i
=
a
n
−
1
+
a
n
−
2
\begin{align*} a_{n}-a_{n-1}&=(\sum_{i=0}^{n-1} \text{fib}_{n-i}\times a_i)-(\sum_{i=0}^{n-2} \text{fib}_{n-i-1}\times a_i)\\ &= a_{n-1} \times \text{fib}_1 + \sum_{i=0}^{n-2}(\text{fib}_{n-i}-\text{fib}_{n-i-1})\times a_i\\ &= a_{n-1}+ \sum_{i=0}^{n-2}\text{fib}_{n-i-2}\times a_i\\ &= a_{n-1}+a_{n-2} \end{align*}
an−an−1=(i=0∑n−1fibn−i×ai)−(i=0∑n−2fibn−i−1×ai)=an−1×fib1+i=0∑n−2(fibn−i−fibn−i−1)×ai=an−1+i=0∑n−2fibn−i−2×ai=an−1+an−2
即
a
i
=
2
×
a
i
−
1
+
a
i
−
2
(
i
>
2
)
a_{i}=2\times a_{i-1}+a_{i-2}\ (i>2)
ai=2×ai−1+ai−2 (i>2)
根据上面的结论可知:
[ a n a n − 1 ] = [ 2 1 1 0 ] n − 2 × [ a 2 a 1 ] \begin{bmatrix} a_{n} \\ a_{n-1} \end{bmatrix}= \begin{bmatrix} 2 & 1\\ 1 & 0 \end{bmatrix}^{n-2}\times\begin{bmatrix} a_{2} \\ a_{1} \end{bmatrix} [anan−1]=[2110]n−2×[a2a1]
利用矩阵快速幂加速即可求得第 n n n 项。时间复杂度为 O ( log n ) O(\log n) O(logn) 。
P = 9614361054979589693
def matrix_mul(a, b):
c = [[0 for _ in range(len(b[0]))] for _ in range(len(a))]
for i in range(len(a)):
for j in range(len(b[0])):
for k in range(len(a[0])):
c[i][j] += a[i][k] * b[k][j] % P
return c
def matrix_pow(a, n):
assert len(a) == len(a[0])
res = [[0 for _ in range(len(a))] for _ in range(len(a))]
for _ in range(len(a)): res[_][_] = 1
while n:
if n % 2 == 1:
res = matrix_mul(res, a)
a = matrix_mul(a, a)
n //= 2
return res
n = int(input())
if n <= 2:
print([1, 2][n - 1])
else:
print(matrix_mul(matrix_pow([[2, 1], [1, 0]], n - 2), [[2], [1]])[0][0] % P)
# [1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461, 80782, 195025, 470832, 1136689, 2744210, 6625109]
D Binary Problem
题目描述
DHR is thinking about how to create a question. He is working out a problem with binary algorithms.
There are n quests. If you complete the i i i-th quest, you will gain a i a_i ai coins. You can only complete at most one quest per day. However, once you complete a quest, you cannot do the same quest again for k k k days. (For example, if k = 2 k=2 k=2 and you do quest 1 1 1 on day 1 1 1, then you can not do it on day 2 2 2 or 3 3 3, but you can do it again on day 4 4 4.)
You are given two integers
c
c
c and
d
d
d. Find the maximum value of
k
k
k such that you can gain at least
c
c
c coins over d days. If no such
k
k
k exists, output Impossible. If
k
k
k can be arbitrarily large, output Infinity.
DHR正在思考如何创造一个问题。他正尝试用二分算法解决一个问题。
有
n
n
n 个任务。如果你完成第
i
i
i 个任务,你将获得
a
i
a_i
ai 的金币。你每天最多只能完成一个任务。然而,一旦你完成了一个任务,你不能再做同样的任务
k
k
k 天。(例如,如果
k
=
2
k=2
k=2 ,你在第一天完成任务
1
1
1 ,那么你就不能在第
2
2
2 天或第
3
3
3 天完成任务
1
1
1 ,但你可以在第
4
4
4 天再次完成任务
1
1
1 。)
给定两个整数
c
c
c 和
d
d
d 。求
k
k
k 的最大值,使你能在
d
d
d 天内获得至少
c
c
c 个硬币。如果这样的
k
k
k 不存在,则输出"Impossible"。如果
k
k
k 可以任意大,输出为"Infinity"。
输入描述:
The first line contains three integers n n n, c c c, d d d ( 2 ≤ n ≤ 2 ⋅ 1 0 5 ; 1 ≤ c ≤ 1 0 1 6 ; 1 ≤ d ≤ 2 ⋅ 1 0 5 2\le n \le 2\cdot10^5;1\le c\le 10^16;1\le d \le 2\cdot 10^5 2≤n≤2⋅105;1≤c≤1016;1≤d≤2⋅105) — the number of quests, the number of coins you need, and the number of days.
The second line contains n n n integers a 1 , a 2 , ⋯ , a n ( 1 ≤ a i ≤ 1 0 9 ) a_1,a_2,\cdots,a_n\ (1\le a_i \le 10^9) a1,a2,⋯,an (1≤ai≤109) — the rewards for the quests.
第一行包含三个整数 n n n, c c c, d d d ( 2 ≤ n ≤ 2 ⋅ 1 0 5 ; 1 ≤ c ≤ 1 0 1 6 ; 1 ≤ d ≤ 2 ⋅ 1 0 5 2\le n \le 2\cdot10^5;1\le c\le 10^16;1\le d \le 2\cdot 10^5 2≤n≤2⋅105;1≤c≤1016;1≤d≤2⋅105) —任务的数量,您需要的硬币的数量和天数。
第二行包含 n n n 个整数 a 1 , a 2 , ⋯ , a n ( 1 ≤ a i ≤ 1 0 9 ) a_1,a_2,\cdots,a_n\ (1\le a_i \le 10^9) a1,a2,⋯,an (1≤ai≤109) ——任务的奖励。
输出描述:
Output one of the following.
- If no such k k k exists, output Impossible.
- If k k k can be arbitrarily large, output Infinity.
- Otherwise, output a single integer — the maximum value of k k k such that you can gain at least c c c coins over d d d days.
输出以下内容之一。
- 如果
k
k
k 不存在,则输出"
Impossible"。 - 如果
k
k
k 可以任意大,输出"
Infinity"。 - 否则,输出一个整数 k k k 的最大值,这样你可以在 d d d 天内获得至少 c c c 个硬币。
示例1
输入
2 20 10
100 10
输出
Infinity
示例2
输入
3 100 3
7 2 6
输出
Impossible
示例3
输入
4 100000000000 2022
8217734 927368 26389746 627896974
输出
12
示例4
输入
2 20 4
5 1
输出
0
首先根据贪心原则,优先选择硬币数多的任务,因此将 a a a 按照从大到小排序。
那么
d
d
d 天获得的硬币数最多为:
∑
i
=
1
min
(
k
+
1
,
n
)
⌈
d
−
i
k
+
1
⌉
×
a
i
\sum_{i=1}^{\min(k+1,n)}\left \lceil \frac{d-i}{k+1} \right \rceil \times a_i
i=1∑min(k+1,n)⌈k+1d−i⌉×ai
显然上式关于 k k k 具有单调性,因此二分最大的 k k k 使得上式不小于 c c c 即可。时间复杂度为 O ( n log d ) O(n \log d) O(nlogd) 。
#include <bits/stdc++.h>
using i64 = long long;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, d;
i64 c;
std::cin >> n >> c >> d;
std::vector<int> a(n);
for (int i = 0; i < n; i++) {
std::cin >> a[i];
}
std::sort(a.begin(), a.end(), std::greater());
if (i64(a[0]) * d < c) {
std::cout << "Impossible\n";
return 0;
}
auto check = [&](i64 k) {
i64 sum = 0;
for (int i = 0; i < std::min(k + 1, i64(n)); i++) {
sum += i64(d - i + k) / (k + 1) * a[i];
}
return sum >= c;
};
i64 l = 0, r = d - 1;
while (l < r) {
i64 m = (l + r + 1) / 2;
if (check(m)) {
l = m;
} else {
r = m - 1;
}
}
if (l == d - 1) {
std::cout << "Infinity\n";
} else {
std::cout << l << "\n";
}
return 0;
}
E Zlz’s problem(Hard Version)
题目描述
This is the easy version of this problem. The only difference between the easy and hard versions is the constraints on n n n and m m m.
So I won’t even take a glance
I would rather do my math
High on some calculus
I can forget about my past
Rather do my math - Robin Gan
Zlz has a bent for mathematics. He once participated in a high school math competition and got the first prize. Even now, he spends a lot of time thinking about mathematical problems. After enjoying the song Rather do my math, Zlz felt more enthusiastic about mathematics. Zlz was playing a card game. There were n cards numbered
1
1
1 to
n
n
n. Each time he randomly selected m cards from these n cards. After that he took down the minimum number of the cards he selected and then put the cards back.
Suddenly, one mathematics problem occurred to him. He wanted to know the expectation of the number he took down. Could you please write a program to calculate the answer modulo
998244353
998244353
998244353.
输入描述:
Only one line contains two integers n , m n,m n,m – the number of cards, the number of cards that Zlz will select.
For most test cases: 1 ≤ n ≤ 2000000 ; 1 ≤ m ≤ n 1\le n\le 2000000;1\le m \le n 1≤n≤2000000;1≤m≤n. For some test cases: n = 1 0 18 , 1 ≤ m ≤ n n=10^{18},1\le m \le n n=1018,1≤m≤n
输出描述:
Output an integer representing the answer modulo 998244353 998244353 998244353 in one line.
示例1
输入
3 2
输出
332748119
示例2
输入
5 3
输出
499122178
根据对本题 Easy Version 版本的分析可知答案为:
∑
i
=
1
n
−
m
+
1
(
n
−
i
m
−
1
)
×
i
(
n
m
)
\frac{\sum\limits_{i=1}^{n-m+1}\binom{n-i}{m-1}\times i}{\binom{n}{m}}
(mn)i=1∑n−m+1(m−1n−i)×i
下面对该式进行化简:
∑
i
=
1
n
−
m
+
1
(
n
−
i
m
−
1
)
×
i
(
n
m
)
=
∑
i
=
1
n
−
m
+
1
∑
j
=
i
n
−
m
+
1
(
n
−
j
m
−
1
)
(
n
m
)
=
∑
i
=
1
n
−
m
+
1
(
n
−
i
+
1
m
)
(
n
m
)
=
(
n
+
1
m
+
1
)
(
n
m
)
=
(
n
+
1
)
!
(
m
+
1
)
!
(
n
−
m
)
!
n
!
m
!
(
n
−
m
)
!
=
n
+
1
m
+
1
\begin{align*} \frac{\sum\limits_{i=1}^{n-m+1}\binom{n-i}{m-1}\times i}{\binom{n}{m}}&=\frac{\sum\limits_{i=1}^{n-m+1}\sum\limits_{j=i}^{n-m+1}\binom{n-j}{m-1}}{\binom{n}{m}}\\ &=\frac{\sum\limits_{i=1}^{n-m+1}\binom{n-i+1}{m}}{\binom{n}{m}}\\ &=\frac{\binom{n+1}{m+1}}{\binom{n}{m}}\\ &= \frac{\frac{(n+1)!}{(m+1)!(n-m)!}}{\frac{n!}{m!(n-m)!}}\\ &=\frac{n+1}{m+1} \end{align*}
(mn)i=1∑n−m+1(m−1n−i)×i=(mn)i=1∑n−m+1j=i∑n−m+1(m−1n−j)=(mn)i=1∑n−m+1(mn−i+1)=(mn)(m+1n+1)=m!(n−m)!n!(m+1)!(n−m)!(n+1)!=m+1n+1
因此答案为
n
+
1
m
+
1
\frac{n+1}{m+1}
m+1n+1 。时间复杂度为
O
(
log
n
)
O(\log n)
O(logn) 。
#include <bits/stdc++.h>
constexpr int N = 2000000;
constexpr int P = 998244353;
using i64 = long long;
// assume -P <= x < 2P
i64 norm(i64 x) {
return x % P;
}
template<class T>
T power(T a, int b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
struct Z {
i64 x;
Z(i64 x = 0) : x(norm(x)) {}
i64 val() const {
return x;
}
Z operator-() const {
return Z(norm(P - x));
}
Z inv() const {
assert(x != 0);
return power(*this, P - 2);
}
Z &operator*=(const Z &rhs) {
x = i64(x) * rhs.x % P;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
friend std::istream &operator>>(std::istream &is, Z &a) {
i64 v;
is >> v;
a = Z(v);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const Z &a) {
return os << a.val();
}
};
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
i64 n, m;
std::cin >> n >> m;
std::cout << Z(n + 1) / Z(m + 1) << "\n";
return 0;
}
F Surveillance System
题目描述
Oops my baby, you woke up in my bed
Oops we broke up, we’re better off as friends
Now I accidentally need you
I don’t know what to do
Oops baby I love you
Oops - Little Mix&Charlie Puth
Dhr had a date with his girlfriend. As the music player was playing Oops, Dhr felt that it was time to propose to his girlfriend. However, when he was looking for the ring he had bought, he found that it had been stolen. Dhr called the cops to find the thief. Unfortunately, the city had no surveillance system and can’t find the trace of thieves.The local government attaches great importance to such theft cases and has decided to establish a secure surveillance system for the region.
To simplify this problem, a region can be seen as a square with side length
n
n
n, where
n
n
n is an even number.
We can divide the region into n × n n \times n n×n units, where 1 1 1 unit is a square with a side length of 1 1 1. The government has decided to choose certain units to install surveillance cameras. After installing a camera in a certain unit, it can monitor its adjacent 4 4 4 units(two units are adjacent if and only if they have a common edge.), as shown in the following figure.
Dhr 在和他女朋友约会,当音响播起 Oops 的时候,Dhr 觉得正式向女朋友求婚的好时机。然而,当他找他买好的戒指的时候发现居然被偷了!他只好报警抓小偷。不幸的是,城市没有安全监控系统,警察没法追查小偷的踪迹。当地政府对于此类偷窃案给予了高度重视,打算建立一个安全全面的监控系统。
为了简化问题,一个地区可以看作边长为
n
n
n 的正方形,
n
n
n 为偶数。我们可以将地区分成
n
×
n
n\times n
n×n 个单位,每个单位是边长为
1
1
1 的正方形。政府准备在某一些单位上安装监控摄像头。一个监控摄像头安装后,它可以检测相邻
4
4
4 个单位的情况,两个单位相邻,当且仅当它们有公共边,如下图所示:
Due to current financial constraints, the government wants to use as few surveillance cameras as possible to ensure that any unit in the region is monitored by at least one surveillance camera.
Note that the surveillance camera can not monitor its own unit, so you must ensure the adjacent unit has at least one surveillance camera to monitor it.
For example, when
n
=
2
n=2
n=2, the answer is
2
2
2. One reasonable surveillance camera arrangement is shown in the following figure.
由于资金紧张,政府想要用尽可能少的摄像头,保证一个地区每个单位都被至少一个摄像头监测到。
注意监控摄像头不能监测到它自己所在的单元,你也必须保证它至少一个相邻单位有摄像头。例如,对于
n
=
2
n=2
n=2 ,答案是
2
2
2 。其中一种合法方案如下图所示:
It can be seen that this arrangement ensures that each unit is monitored by at least one surveillance camera.
可以证明这种方案可以保证每个单位都有监控摄像头监测到。
输入描述:
Each test contains multiple test cases. The first line contains the number of test cases
t
t
t.
The only line of each testcase contains one integer
n
n
n, represents the length of the square region.
It’s guaranteed that
n
n
n is even,
2
≤
n
≤
1000000000
2\le n\le 1000000000
2≤n≤1000000000, and
1
≤
t
≤
100000
1\le t \le 100000
1≤t≤100000.
本题一个测试点含有多个测试数据,第一行一个整数 t t t 表示测试数据个数。
下面 t t t 行每行一个正整数 n n n ,表示正方形区域的长。
题目保证: n n n 为偶数, 2 ≤ n ≤ 1000000000 2\le n\le 1000000000 2≤n≤1000000000
1 ≤ t ≤ 100000 1\le t \le 100000 1≤t≤100000.
输出描述:
Output an integer representing the answer in one line for each test.
每一个测试输出一行整数表示答案。
示例1
输入
2
2
4
输出
2
6
由于图形中间空缺的位置需要填补,因此可以确定最终方案一定有下面两种图形组成。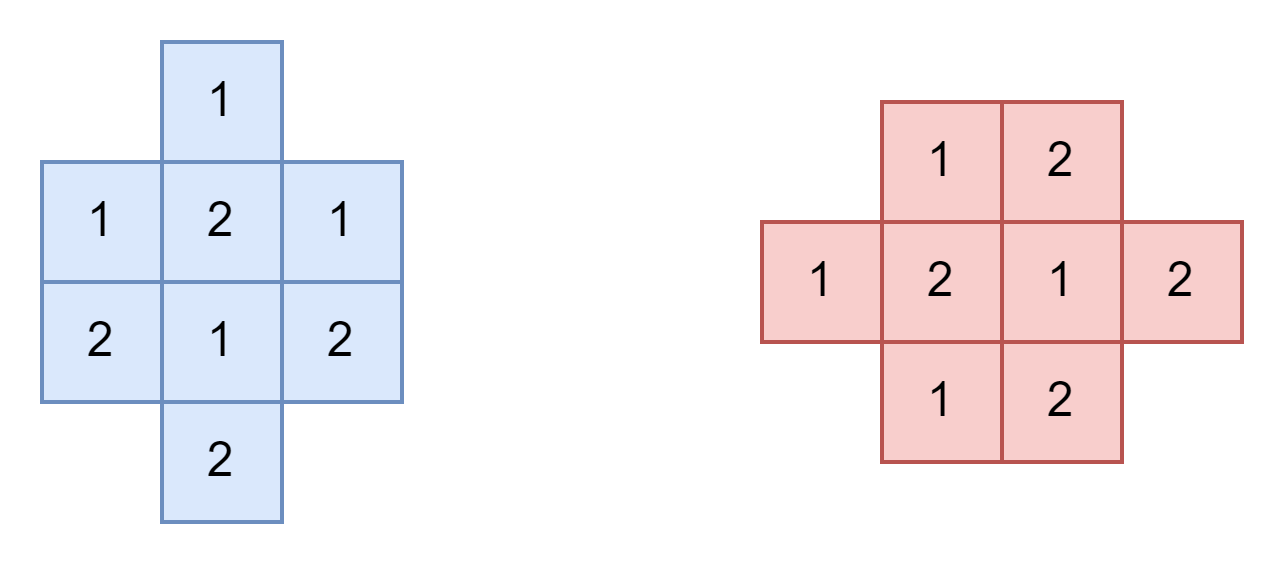
通过构造发现,总能通过增加上面的两种图形来从覆盖边长为
n
n
n 的正方形的方案转换为覆盖边长为
n
+
2
n+2
n+2 的正方形的方案,并且不会存在图形重叠的情况。该方案所需摄像头的数量为
n
×
(
n
+
2
)
4
\frac{n\times (n+2)}{4}
4n×(n+2) 。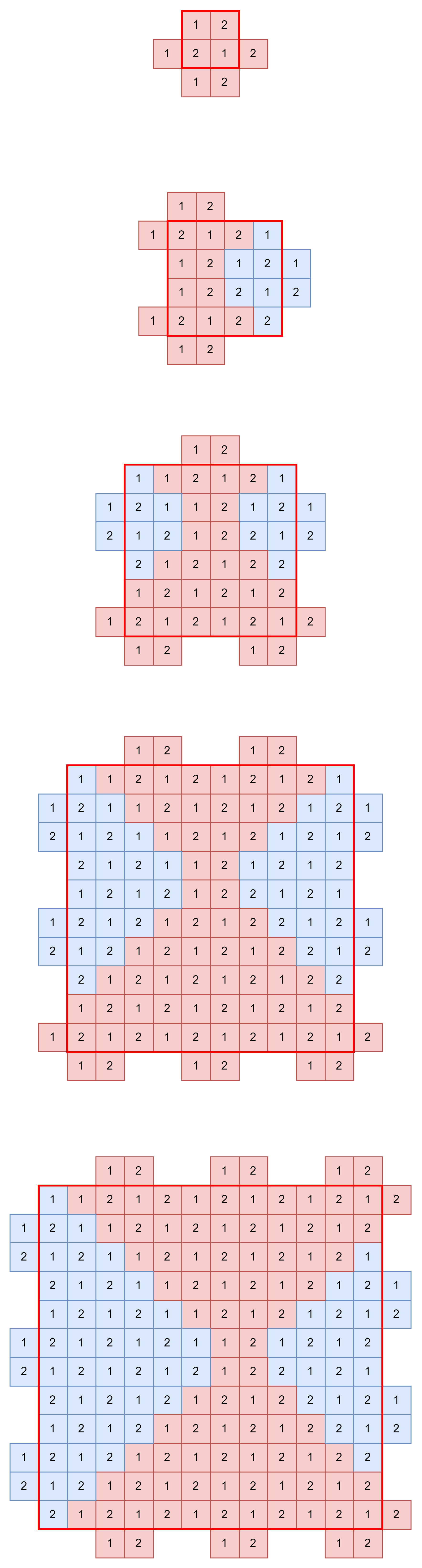
#include <bits/stdc++.h>
using i64 = long long;
void solve() {
int n;
std::cin >> n;
std::cout << i64(n) * (n + 2) / 4 << "\n";
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}
G Koyuki’s problem
题目描述
いつか好きになる気づいた
あと何回ねえ目が合えば
カウントダウン止まって
認めたら認めちゃったら
隠す声が震えちゃうんだ
今好きになる
今好きになる - HoneyWorks
One day Hina made up her mind to profess her love to Koyuki. Koyuki, as a senior, was going to prepare a simple problem to test her. Once upon a time, Gauss’s teacher asked him to calculate the sum of
1
1
1 to
100
100
100. And Gauss came up with the summation formula. Koyuki also wanted Hina to calculate the sum of some numbers. To keep Hina away from the summation formula, Koyuki gave Hina some integers and operation symbols. There are only two types of operation symbols: addition and subtraction. The value was equal to zero from the beginning. Hina had to use all of the operation symbols and choose some integers Koyuki gave to maximize the value.
This problem was too computationally demanding for Hina. So she hopes you can write a program to help her calculate the answer within one second.

Hina 终于鼓起勇气向 Koyuki 表白,Koyuki 作为高年级学长,准备用一个简单的问题考考 Hina 。想当年高斯的老师让他的学生们计算 1 1 1 到 100 100 100 的和,结果高斯总结出了求和公式。Koyuki 也想让 Hina 算一些数的和,为了防止她用求和公式,Koyuki 给出一些整数和一些运算符号,运算符号只有加和减两种。初始值为 0 0 0 ,Hina 需要使用完所有的运算符号,使得最后的运算值尽可能的大。
这个问题对于 Hina 来说计算量太大了,所以她希望你能写一个程序帮她一秒之内算出答案。
输入描述:
The first line contains three integers n , p , q n,p,q n,p,q – the number of given integers, the number of given plus signs, the number of given minus signs.
The second line contains
n
n
n integers
a
1
,
a
2
,
⋯
,
a
n
a_1,a_2,\cdots,a_n
a1,a2,⋯,an – the integers that Koyuki gave.
All the integers are separated by a blank space.
It is guaranteed that for all test cases: 1 ≤ n ≤ 2000000 ; − 1 0 9 ≤ a ≤ 1 0 9 ; p + q ≤ n ; p , q ≥ 0 1\le n \le 2000000;-10^9\le a\le 10^9;p+q\le n;p,q\ge 0 1≤n≤2000000;−109≤a≤109;p+q≤n;p,q≥0
第一行包含 3 3 3 个整数 n , p , q n,p,q n,p,q ,分别表示给定数字的数量,加号数量,减号数量.
第二行 n n n 个整数, a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an ,表示 Koyuki 给出的数。
保证所有的测试点满足:
1
≤
n
≤
2000000
;
−
1
0
9
≤
a
≤
1
0
9
;
p
+
q
≤
n
;
p
,
q
≥
0
1\le n \le 2000000;-10^9\le a\le 10^9;p+q\le n;p,q\ge 0
1≤n≤2000000;−109≤a≤109;p+q≤n;p,q≥0
输出描述:
Output an integer representing the answer in one line.
一行一个整数表示答案。
示例1
输入
5 1 2
6 0 1 2 2
输出
5
示例2
输入
7 5 2
1 2 3 4 5 6 7
输出
22
贪心的将加号分配到尽可能大的数,减号分配到尽可能小的数即可。时间复杂度为 O ( n log n ) O(n\log n) O(nlogn) 。
#include <bits/stdc++.h>
using i64 = long long;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, p, q;
std::cin >> n >> p >> q;
std::vector<i64> a(n);
for (int i = 0; i < n; i++) {
std::cin >> a[i];
}
std::sort(a.begin(), a.end());
std::cout << std::accumulate(a.rbegin(), a.rbegin() + p, 0LL) - std::accumulate(a.begin(), a.begin() + q, 0LL) << "\n";
return 0;
}
H GTA Ⅲ
题目描述
Tell me why, ain’t nothin’ but a heartache
Tell me why, ain’t nothin’ but a mistake
Tell me why, I never wanna hear you say
I want it that way
I Want It That Way - Backstreet Boys
Hxt was playing GTA Ⅲ. He felt he was racing on the streets of Liberty City while enjoying I Want It That Way. He had to pass a mission. His job, decoy, to distract the cops. Hxt decided to choose a starting point, and drive clockwise along the loop once and then return to this place. There are some tools along the way. When the vehicle encounters one tool, its durability will be increased by
1
1
1. The cops, however, placed roadblocks on the roundabout. When the vehicle encounters one roadblock, its durability will be decreased by
1
1
1. The vehicle will explode when its durability becomes
0
0
0. Unfortunately, the vehicle that Hxt drove had only one durability left due to being attacked by cops. He hope to find a place to start and ensure the safety of his vehicle.
To simplify the problem, Hxt will choose the starting place at one of the tool.
Hxt 正在玩 GTA Ⅲ 。他感觉自己听着 I Want It That Way 在自由城的街道上狂飙。他需要完成一个任务,在这个任务中他会作为诱饵引开警察。打算选择一个起始点,在一个环道上顺时针方向溜一圈回到这个点。在环道上有一些修车道具,当车辆触碰到道具时,耐久度就会加 1 1 1 。但是警察会在环道上放一些路障,当车辆触碰到路障时,耐久度就会减少 1 1 1 。 当车辆耐久度为 0 0 0 时就会爆炸。不幸的是,Hxt 驾驶的车辆在之前受到了警察的攻击, 耐久度只有 1 1 1 了。他希望能找到一个安全的起始点,确保他的车辆安全顺利完成任务。
为了简化问题,Hxt 会将起始地点选在某一个修车道具上。
输入描述:
The first line contains one integer n n n – the number of tools and roadblocks.
The second line contains a string of length n. The string only contains char ‘0’ and ‘1’. ‘1’ represents a tool and ‘0’ represents a roadblock. The string represents starting from a certain point, the situation of various roadblock or tools in a clockwise direction.
For example, if the string is ‘100110’, it can represent this case:
It is guaranteed that for all test cases:
1
≤
n
≤
5000000
1\le n\le 5000000
1≤n≤5000000
第一行一个整数 n n n 1 ≤ n ≤ 5000000 1\le n\le 5000000 1≤n≤5000000表示修车道具和路障的总数。
第二行一个长度为
n
n
n 的字符串,字符串仅包含’0’和’1’两种字符。 ‘1’ 表示工具, ‘0’ 表示路障。字符串表示从一个点出发,顺时针沿着环道走一圈,沿途的道具和路障出现的情况。
例如,如果字符串为 ‘100110’,就可以表示下图路况:
输出描述:
Output the index of the starting place you find in the string. Output − 1 -1 −1 if you can’t find any. If there are multiple solutions, print the minimum of them.
Note that the index of the string starts from 1 1 1.
输出你找到的起点在字符串中出现的下标位置。如果没找到输出 − 1 -1 −1 ,如果有多个解,输出最小的一个。
注意字符串下标从 1 1 1 开始。
示例1
输入
6
100110
输出
4
示例2
输入
14
01101011010010
输出
2
即寻找一个最小的下标,从该下标开始长度为 n n n 的前缀和不能有小于 0 的项。可以用单调队列维护长度为 n n n 的区间中前缀和最小的项,时间复杂度为 O ( n ) O(n) O(n) 。
#include <bits/stdc++.h>
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n;
std::string s;
std::cin >> n >> s;
std::vector<int> sum(n * 2 + 1);
for (int i = 0; i < n * 2; i++) {
sum[i + 1] = sum[i] + (s[i >= n ? i - n : i] == '0' ? -1 : 1);
}
std::deque<int> q;
for (int i = 1; i <= n; i++) {
while (!q.empty() && sum[i] <= q.back()) {
q.pop_back();
}
q.push_back(sum[i]);
}
for (int i = 0; i < n; i++) {
if (!q.empty() && q.front() >= sum[i]) {
std::cout << i + 1 << "\n";
std::exit(0);
}
while (!q.empty() && sum[i + n + 1] <= q.back()) {
q.pop_back();
}
q.push_back(sum[i + n + 1]);
}
std::cout << -1 << "\n";
return 0;
}
I Card game
题目描述
Some day
いつか辿り着ける
きっと君に寄り添うため
何度もすれ違い
それでも信じて
道の先、空の向こう - Rita
Sora is playing a card game with Haruka.
There are n n n piles of cards on the table. And there is a positive integer on each card. The players take turns and Sora takes the first turn. In Sora’s turn she takes a card from the top of any non-empty pile, and in Haruka’s turn he takes a card from the bottom of any non-empty pile. Each player wants to maximize the total sum of the cards he took. The game ends when all piles become empty.
Suppose Sora and Haruka play optimally, what is the score of the game?
Sora 和 Haruka 正在玩卡牌游戏,桌子上有 n n n 堆卡牌,每个卡片上都写有一个正整数。
两名玩家轮流取牌,Sora 先取。Sora 可以从任何非空牌堆的顶部取出一张牌,Haruka 可以从任何非空牌堆的底部取出一张牌。当所有的牌堆都变空时游戏结束。他们都想最大化他所拿牌的分数(即每张牌上正整数的和)。如果 Sora 和 Haruka 每一步都选择最优,问他们所拿牌的分数分别是多少?
输入描述:
The first line contain an integer n ( 1 ≤ n ≤ 100 ) n\ (1\le n \le 100) n (1≤n≤100). Each of the next n n n lines contains a description of the pile: the first integer in the line is s i ( 1 ≤ s i ≤ 100 ) s_i\ (1\le s_i \le 100) si (1≤si≤100) — the number of cards in the i i i-th pile; then follow s i s_i si positive integers c 1 , c 2 , ⋯ , c k , ⋯ , c s i ( 1 ≤ c k ≤ 1000 ) c_1,c_2,\cdots,c_k,\cdots,c_{s_i}\ (1\le c_k\le 1000) c1,c2,⋯,ck,⋯,csi (1≤ck≤1000) — the sequence of the numbers on the cards listed from top of the current pile to bottom of the pile.
第一行一个整数 n ( 1 ≤ n ≤ 100 ) n\ (1\le n \le 100) n (1≤n≤100) ,表示卡片的堆数,下面 n n n 行每一行的格式如下:第一个整数 s i ( 1 ≤ s i ≤ 100 ) s_i (1\le s_i \le 100) si(1≤si≤100) 表示第 i i i 堆的卡片个数, s i s_i si 个正整数 c 1 , c 2 , ⋯ , c k , ⋯ , c s i ( 1 ≤ c k ≤ 1000 ) c_1,c_2,\cdots,c_k,\cdots,c_{s_i}\ (1\le c_k\le 1000) c1,c2,⋯,ck,⋯,csi (1≤ck≤1000) 表示从上到下每个卡片上的数字。用空格分开。
输出描述:
Print two integers: the sum of Sora’s cards and the sum of Haruka’s cards if they play optimally.
输出两个整数用空格分开,分别表示 Sora 最终得分和 Haruka 最终得分。
示例1
输入
2
1 100
2 1 10
输出
101 10
示例2
输入
1
9 2 8 6 5 9 4 7 1 3
输出
30 15
示例3
输入
3
3 1 3 2
3 5 4 6
2 8 7
输出
18 18
首先不考虑奇数牌堆中中间的那一个牌。那么最终结果如下:
- 对于 s i s_i si 为偶数的情况,一定是前一半被 Sora 拿走,后一半被 Haruka 拿走;
- 对于 s i s_i si 为奇数的情况,除了中间那一个外也是前一半被 Sora 拿走,后一半被 Haruka 拿走。
因为首先假设有一种分配方案与对半分时双方的优势相同,那么该方案对应的答案与对半分相同;假设有一种分配方案与对半分时双方的优势不同那么一定有优势的一方和劣势的一方,劣势的一方一定通过模仿优势的一方的取牌方案来阻止优势的一方。如果在阻止的过程中劣势的一方优势大于对半分的情况也会被另一方通过模仿策略来阻止,最终的结果是双方还是对半分。文章来源:https://uudwc.com/A/0rxR5
因此此时的问题变为讨论 s i s_i si 为奇数的情况下中间的那一张牌如何分配。显然对于某一堆卡片,先手的可以拿到中间的卡片,同时在取下一堆卡片变为后手,因此将 s i s_i si 为奇数的牌堆的中间的卡片进行排序,则双方一次从大到小取得这些卡片。文章来源地址https://uudwc.com/A/0rxR5
#include <bits/stdc++.h>
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n;
std::cin >> n;
int ans1 = 0, ans2 = 0;
std::vector<int> a;
for (int i = 0; i < n; i++) {
int s;
std::cin >> s;
for (int j = 0; j < s; j++) {
int c;
std::cin >> c;
if (j < s / 2) {
ans1 += c;
} else if (j == s / 2) {
if (s % 2 == 1) {
a.push_back(c);
} else {
ans2 += c;
}
} else {
ans2 += c;
}
}
}
std::sort(a.begin(), a.end(), std::greater());
for (int i = 0; i < a.size(); i++) {
if (i % 2 == 0) {
ans1 += a[i];
} else {
ans2 += a[i];
}
}
std::cout << ans1 << " " << ans2 << "\n";
return 0;
}