三种方法：
- 递推方法求递归算法的时间复杂性
- Master定理方法求递归算法时间复杂性
- 递归树求解递归方程
文章来源地址https://uudwc.com/A/4M9y
1.递推方法求递归算法的时间复杂度
我们先来看一个经典的案例，汉诺塔问题
汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？
相信大家都见过这个问题，我就不多加赘述了，没有看过的可以可以查看一下下面的资料
汉诺塔问题
我们给出伪代码
算法 Hanoi (?,?,n) // n个盘子?到?
if n = 1 then move (?,?) // 1个盘子?到?
else Hanoi (?,?,n − 1)
move (?,?)
Hanoi (?,?,n − 1)时间复杂度：
我们使用递推法求事件复杂度：
这时候我们发现，汉诺塔问题的时间复杂度是指数级别的。
2.Master定理方法求递归算法时间复杂性
在常见的分治算法中，我们通常设计为递归算法。
关于分治算法，可以查看下面这个博客：
分治算法
其事件复杂度的递归定义通常有如下形式：
使用master定理可以快速求解该方程
这里要求a >= 1, b > 1为整数，f(n)是正函数
方法如下：
我们先来分析三个规则，规则1对应大于，规则2对应等于，规则3对应小于
规则1举例：
规则2举例：
我们取计算机算法设计与分析第五版第二章合并算法来分析
pdf地址：http://jxz1.j9p.com/pc/jsjsfyfx5.pdf
规则3举例：
这个例子很简单，为了更深度的理解规则3，我们在举一个例子
解法：
当看到我们老师给出这个解法的时候，我很纳闷，为什么ε要取0.2
我搜索了很多资料
证明方法
20个训练题目（附答案）
看完这些之后，我悟了，原来是我没有明白O、Ω、θ三个符号的意义，这里给出定义
而我们规则3的定义是
下界Ω
按照我的理解就是只要f(n)的阶层比
高即可
那么我们取0.1也是可以的
但是如果我们取0.3就不可以了，因为当取0.3的时候，n的指数就大于1了，当n无穷大时，取极限，它的数值大于nlogn，所以n的指数只能小于1
再看一个例子：
3.递归树求解递归方程
递归树的规则为：
(1) 每层的节点为T(n) = kT(n / m) + f(n)中的f(n)在当前的n/m下的值；
(2) 每个节点的分支数为k；
(3)每层的右侧标出当前层中所有节点的和。
举一个例子：
再举个例子：
T(n) = T(n/3) + T(2n/3) + n
其递归树如下图所示：
可见每层的值都为n，从根到叶节点的最长路径是：
因为最后递归的停止是在(2/3)kn == 1.则
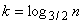
于是
即T(n) = O(nlogn)
文章中图片来源：张舒老师的课件（感谢！！！）文章来源：https://uudwc.com/A/4M9y
