无约束的遗传算法（最简单的）
最开始真正理解遗传算法，是通过这个博主的讲解，安利给小白们看一看，遗传算法的Python实现（通俗易懂），我觉得博主写的让人特别容易理解，关键是代码也不报错，然后我就照着他的代码抄了一遍，认真地理解了一下每一个模块，：编码、解码、适应度函数写法、选择、交叉和变异的实现过程，下面也谈一谈我在整个过程中的认识，以及对代码的一种通俗解释：
1、编码：这里主要运用的就是一种二进制的编码，将要求解的问题的解，从十进制的自然数以某一种方式用二进制表达出来，每一个0或1作为是一个基因位，一个数的众多基因构成一条染色体，也就是一个个体，进而众多染色体构成一个种群，所说的种群规模其实就是这些染色体的个数，最后用这个种群去参与到遗传算法的各个过程中，并且二进制的编码对于交叉和变异的操作会简单一点。
2、解码：因为适应度函数是用十进制的自然数写的，所以在每一次迭代中，要把二进制的染色体，再变成十进制的数，才能参与到适应度的计算中，就照着解码公式写出来就好了。
##解码函数
def decode(pop):
return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) *(X_max-X_min)/ float(2**DNA_SIZE-1) +X_min
3、适应度函数：作为遗传变异的根据，这个函数通常跟我们目标函数有关系，因为后面在选择过程中，是保留适应度值更大的个体，所以适应度值我们都认为是越大越好，那么目标函数是求最大值的时候，那也就是说适应度值越大，越接近目标，所以令适应度函数=目标函数。
目标函数求最小值时，如果也想达到这样的效果，则令适应度函数=1/目标函数。
但是在这里又遇到了一个问题，因为适应度值必须是正的，因为要求占比，但目标函数值有可能是负的，所以就做了下面的这个转换，让求出来的适应度值是正的，并且与目标函数值的变化是一致的，如果以后遇到的话，也可以尝试着自己去想表达式来解决，只要明白这个目的。
"""求解的目标表达式为：
y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)
x=[0,5]
"""
def aim(x):
return 10*np.sin(5*x)+7*np.cos(4*x)
##适应度计算函数
def fitnessget(pred):
return pred + 1e-3 - np.min(pred)
4、选择：最常用的就是轮盘赌方式，了解完他的定义之后发现他的代码实现也不难，比如有五个个体的种群，索引序号是[0,1,2,3,4]，那就是计算适应度值，并且求一下在总的适应度里面的占比，得到[0.1,0.2,0.3,0.1,0.3],然后根据这每一个个体的比例来随机抽数，得到[2,4,2,1,4],就比如两个0.3的概率最大，那么抽取到个体2和4的概率就更大，最终根据这个序号去选择种群中对应的个体，进行保留到下一代，这就实现了适应环境的留下，不适应的淘汰。
##自然选择函数（轮盘赌）
def select(pop, fitness):
# print(abs(fitness))
# print(fitness.sum())
idx = np.random.choice(np.arange(pop_size), size=pop_size, replace=True,p=fitness/fitness.sum())
# print(idx)
return pop[idx]
4、交叉：二进制的交叉就是针对每一个个体，随机找到一个个体，然后再随机找到某几个基因位，这两个个体的这些基因位进行交换，这里我看的时间比较久，实在不懂就打印出来看看是啥咯
def change(parent, pop):
x = np.random.rand()
print('x:{}'.format(x))
if x < PC: #交叉
i_ = np.random.randint(0, pop_size, size=1) ##随机找到要与之交叉的某一行，也就是某另一个个体
print('i_:{}'.format(i_))
cross_points = np.random.randint(0, 2, size=DNA_SIZE)##生成一个只有0和1的列表，长度等于基因长度
print('cross_points:{}'.format(cross_points))
cross_points = cross_points.astype(np.bool) ##1的地方就是True
print('cross_points:{}'.format(cross_points))
print(np.where(cross_points==True)) ##np.where()就是找到True的地方，就是用这种方法来找到1的地方，作为交叉的基因位
print('cross_points:{}'.format(cross_points))
print('parent[cross_points]:{}'.format(parent[cross_points]))
parent[cross_points] = pop[i_, cross_points]
print('parent:{}'.format(parent))
return parent
5、变异：二进制的变异就很简单了，就是选择基因位，然后0变成1,1变成0，代码也比较容易实现。
def variation(child,pm): #变异
for point in range(DNA_SIZE):
if np.random.rand() < pm:
child[point] = 1 if child[point] == 0 else 0
# print(child)
return child
6、遗传算法主体
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
##定义全局变量
pop_size = 5 # 种群数量
PC=0.6 # 交叉概率
PM=0.01 #变异概率
X_max=5 #最大值
X_min=0 #最小值
DNA_SIZE=10 #DNA长度与保留位数有关,2**10 当前保留3位小数点，这个应该是二进制考虑的问题，保留的规则可以去搜一下，有的实际问题需要实数编码的话，就直接看着所要求的问题设置编码长度就好了
N_GENERATIONS=100 ##迭代次数
##生成初始解，这个初始种群就是一个可行解的集合，在这样的条件下进行选择、交叉和变异操作，选出最适应当前环境的个体，也就得到了我们的最优解
pop = np.random.randint(2, size=(pop_size, DNA_SIZE)) ###得到初始化种群
# print(pop)
X = np.arange(0,N_GENERATIONS,1)
Y = [None]*N_GENERATIONS ##先产生一个全部都是0的列表，用于存放每一次迭代的最优值，最后进行画图展示迭代过程
for i in range(N_GENERATIONS): ##上面写的选择、交叉、变异都是在一次进化中的操作，每一次迭代都要进行
#解码
# print(pop)
X_value= decode(pop)
#获取目标函数值
F_values = aim(X_value)
#获取适应值
fitness = fitnessget(F_values)
# print(fitness)
if(i==0):
max=np.max(F_values)
max_DNA = pop[np.argmax(F_values), :] ##取取得适应度最大值的那个个体
if(max<np.max(F_values)):
max=np.max(F_values)
max_DNA=pop[np.argmax(F_values), :]
if (i % 10 == 0):
print("Most fitted value and X: \n",
np.max(F_values), decode(pop[np.argmax(F_values), :]))
#选择
pop = select(pop,fitness)
# print(pop)
pop_copy = pop.copy()
# print(pop_copy)
for index,parent in enumerate(pop):
# print(parent)
child = change(parent,pop_copy)
child = variation(child,PM)
# print(child)
pop[index] = child
Y[i] = max
print("目标函数最大值为：",max)
print("其DNA值为：",max_DNA)
print("其X值为：",decode(max_DNA))
plt.plot(X,Y)
结果如下：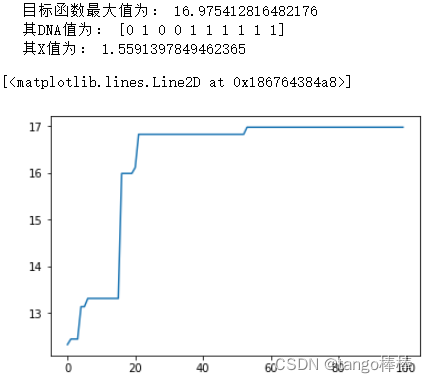
文章来源：https://uudwc.com/A/59A4J
好了，大家把上面的代码和解释全部认真读一遍，小白也能懂遗传算法了。文章来源地址https://uudwc.com/A/59A4J
