Bentley-Ottmann算法：求N条线段的交点

Bentley-Ottmann算法

如果说你想知道这个方法的历史，那么推荐几篇远古论文：

1. 来自Michael Ian Shamos和Dan Hoey在1976年发表的：
   M. I. Shamos and D. Hoey, “Geometric intersection problems,” 17th Annual Symposium on Foundations of Computer Science (sfcs 1976), 1976, pp. 208-215, doi: 10.1109/SFCS.1976.16.
   上链接：
   http://euro.ecom.cmu.edu/people/faculty/mshamos/1976GeometricIntersection.pdf
2. 作者Bentley和Ottmann改进了上面的方法：
   Bentley and Ottmann, “Algorithms for Reporting and Counting Geometric Intersections,” in IEEE Transactions on Computers, vol. C-28, no. 9, pp. 643-647, Sept. 1979, doi: 10.1109/TC.1979.1675432.
   上链接：http://www.itseng.org/research/papers/topics/VLSI_Physical_Design_Automation/Physical_Verification/DRC/Geometric_Intersection_Problems/1979-Bentley.pdf

算法复杂度

我们求N条线段中任意两条线段的交点的个数：

1. 使用暴力求解，遍历每一条线段 i ，固定 i 遍历 j 与 i 是否存在交点：

// 暴力求解
for(int i = 0; i < segment.size(); i++)
{
	for(int j = 0; j < segment.size(); j++)
	{
		//判断是否相交
	}
}

算法时间复杂度为：$O(n^2)$
$T(n)=(n+n+n+...+n)=n^2$

2. 此时我们可以稍微优化一点算法复杂度，判断过 i, j 是否相交以后，j, i 就不用再判断了：

// 优化
for(int i = 0; i < segment.size(); i++)
{
	for(int j = i; j < segment.size(); j++)
	{
		//判断是否相交
	}
}

算法时间复杂度为：$O(n^2)$
$T(n)=(1+2+3+...+n)=\frac{n^2+n}{2}$

3. Bentley-Ottmann算法

排序算法时间复杂度为：$O(nlogn)$
使用平衡二叉树进行插入、删除操作，时间复杂度为：$O(logn)$
事件队列最多存储$2\ast n+x$个点
（事件队列是什么意思？在算法案例中将讲解）
所以Bentley-Ottmann算法时间复杂度最大为：$O((2n+i)logn)=O(nlogn)$

算法案例（流程）

我们通过讲解下面这个案例来理解算法：如果想直接看论文转下
论文案例链接：
http://www.ams.sunysb.edu/~jsbm/courses/345/13/bentley-ottmann.pdf

1. 问题描述

给定7条线段，用$S$表示
$$\begin{array}{rl}S& =s_0,s_1,...,s_6\\ & =\{((15,17),(7,3)),((3,16),(6,10)),((2,15),(12,8)),((7,14),(11,6)),\\ & ((10,13),(2,4)),((1,12),(9,5)),((-3,11),(5,2))\}\end{array}$$
每条线段用$s_i=(a_i,b_i)$表示，$a_i$表示起始点，$b_i$表示末尾点。
如图：Joe Mitchell的例子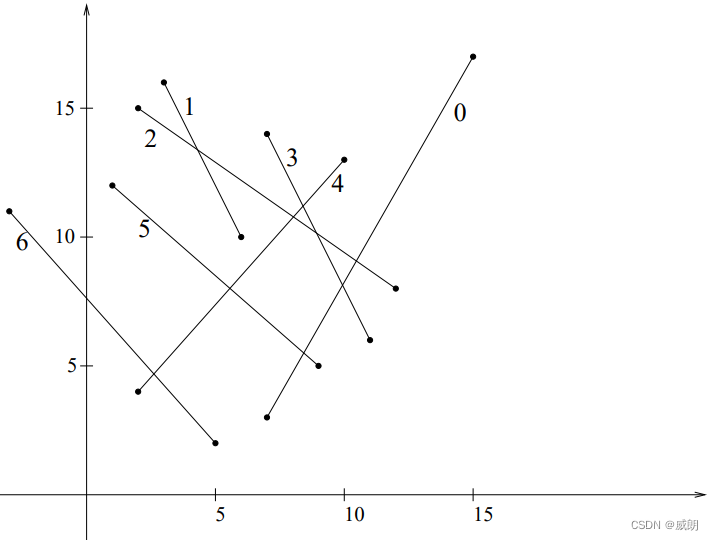

2. 名词介绍

（1）Event Queue（事件队列）：后续用Q表示

该算法通过维护一个队列的入队、出队来求所有的交点，而该队列称为事件队列。

（2）Sweep Status（扫描线）：后续用L表示

使用一条平行于 $x$ 轴或者平行于 $y$ 轴的直线遍历所有线段的端点以及交点，有图有真相：

（3） 交点：用 $x_{ij}$ 表示，$i,j$ 表示相交的两条线段的下标

3. 案例讲解

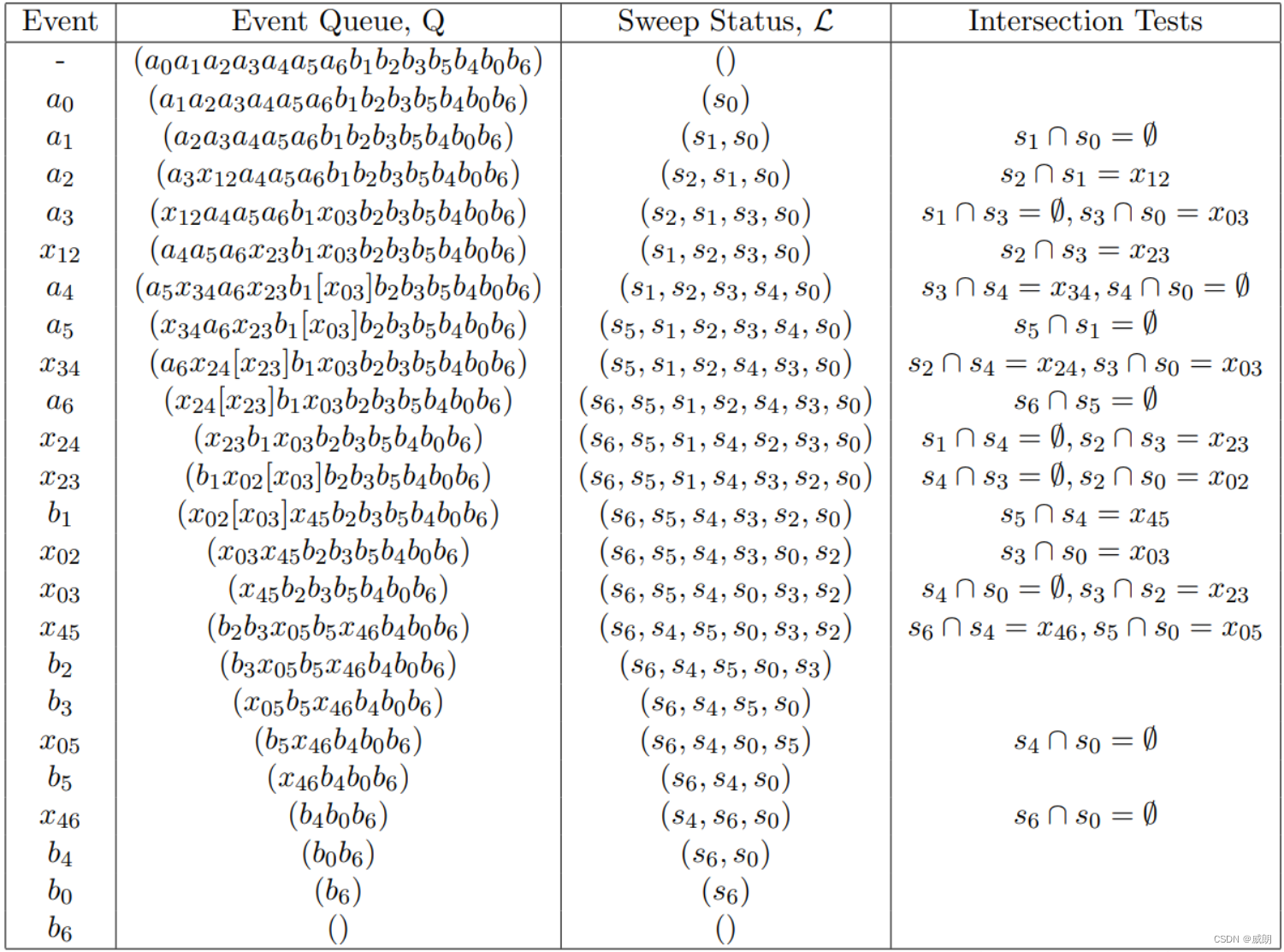
（1）排序： 将所有端点按照 $y$ 坐标大小进行排序，存在 $Q$ 中，得到第 “-” 行。案例按照 $y$ 从大到小排序

（2）3个原子操作：

a. 当扫描线扫描到线段初始点时，进行出队操作，取出队顶元素，判断相邻线段与当前线段是否相交。相交时将交点入队，将其插入到按 $y$ 排序的队列中；

假如当前 $L=(s_2,s_1,s_3,s_0)$，判断 $s_1$ 与相邻线段 $s_2、s3$ 是否相交。

b. 当扫描线扫描到线段交点时，将交点 $x_{ij}$ 进行出队操作，并且将 $L$ 中对应的 $i,j$ 交换位置，在重新判断 $i,j$ 与各自相邻线段是否相交，相交时，将其插入到按 $y$ 排序的队列中；

c. 当扫描线扫描到线段末尾点时，将右端点进行出队操作，从 $L$ 中将 $s_i$ 去除。此时判断与 $s_i$ 相邻的两个线段是否相交，相交时，将其插入到按 $y$ 排序的队列中。

（3）按照表格左侧 Event 来解析每一步的含义

1. 扫描线扫描到 $a_0$，从队列 $Q$ 中出队，将 $a_0$ 所对应的线段 $s_0$ 添加到 $L$ 中，$L$ 中只有一条线段，无需判断是否相交；
   

2. 扫描线扫描到 $a_1$，从队列 $Q$ 中出队，将 $a_1$ 所对应的线段 $s_1$ 添加到 $L$ 中，$L$ 中有两条线段，判断是否相交，结果不相交，进行下一步；
   注意：此时问题来了，将 $s_1$ 添加到 $s_0$ 的前面还是后面呢？
   答：按照扫描线的 $x$ 的大小，从小到大排序。
   现在 $L$ 经过了 $s_0,s_1$ 将扫描线与 $s_0,s_1$ 的交点按照 $x$ 从小到大排序。将 $s_1$ 放在 $s_0$ 前面。
   

3. 扫描线扫描到 $a_2$，从队列 $Q$ 中出队，将 $a_2$ 所对应的线段 $s_2$ 添加到 $L$ 中（按照 $x$ 升序添加：$L=(s_2,s_1,s_0)$），$L$ 中有三条线段，判断 $s_2$ 与相邻线段 $s_1$ 是否相交（注意，此时 $s_2$ 在 $L$ 中相邻的线段只有 $s_1$， 而没有 $s_5$ ），结果相交，将交点 $x_{12}$插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
   

4. 扫描线扫描到 $a_3$，从队列 $Q$ 中出队，将 $a_3$ 所对应的线段 $s_3$ 添加到 $L$ 中（按照 $x$ 升序添加：$L=(s_2,s_1,s_3,s_0)$），$L$ 中有四条线段，判断 $s_3$ 与相邻线段 $s_1、s_0$ 是否相交，结果 $s_3$ 与 $s_0$ 相交，将交点 $x_{03}$插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
   

5. 扫描线扫描到交点 $x_{12}$，从队列 $Q$ 中出队，交换 $L=(s_2,s_1,s_3,s_0)$ 中交点所对应的线段 $s_1,s_2$ 的位置： $L=(s_1,s_2,s_3,s_0)$，重新判断 $s_1,s_2$ 与各自的相邻线段是否存在交点，此时 $s_2$ 与相邻线段 $s_3$ 相交，将交点 $x_{23}$ 插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
   

6. 扫描线扫描到 $a_4$，从队列 $Q$ 中出队，将 $a_4$ 所对应的线段 $s_4$ 添加到 $L$ 中（按照 $x$ 升序添加：$L=(s_1,s_2,s_3,s_4,s_0)$，$L$ 中有五条线段，判断 $s_4$ 与相邻线段 $s_3、s_0$ 是否相交，结果 $s_4$ 与 $s_3$ 相交，将交点 $x_{34}$插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
   

7. 扫描线扫描到 $a_5$，从队列 $Q$ 中出队，将 $a_5$ 所对应的线段 $s_5$ 添加到 $L$ 中（按照 $x$ 升序添加：$L=(s_5,s_1,s_2,s_3,s_4,s_0)$，$L$ 中有六条线段，判断 $s_5$ 与相邻线段 $s_1$ 是否相交，结果 $s_5$ 与 $s_1$ 不相交，转下一步；
   

8. 扫描线扫描到交点 $x_{34}$，从队列 $Q$ 中出队，交换 $L=(s_5,s_1,s_2,s_3,s_4,s_0)$） 中交点所对应的线段 $s_3,s_4$ 的位置：$L=(s_5,s_1,s_2,s_4,s_3,s_0)$，重新判断 $s_3,s_4$ 与各自的相邻线段是否存在交点
   此时 $s_3$ 与相邻线段 $s_0$ 相交，但是 $x_{03}$ 已经存在于队列 $Q$ 中了，所以不用重新加入；
   $s_4$ 与相邻线段 $s_2$ 相交，将交点 $x_{24}$ 插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
   

9. 扫描线扫描到 $a_6$，从队列 $Q$ 中出队，将 $a_6$ 所对应的线段 $s_6$ 添加到 $L$ 中（按照 $x$ 升序添加：$L=(s_6,s_5,s_1,s_2,s_4,s_3,s_0)$，$L$ 中有七条线段，判断 $s_6$ 与相邻线段 $s_5$ 是否相交，结果 $s_5$ 与 $s_1$ 不相交，转下一步；
   

10. 扫描线扫描到交点 $x_{24}$，从队列 $Q$ 中出队，交换 $L=(s_6,s_5,s_1,s_2,s_4,s_3,s_0)$ 中交点所对应的线段 $s_2,s_4$ 的位置：$L=(s_6,s_5,s_1,s_4,s_2,s_3,s_0)$，重新判断 $s_2,s_4$ 与各自的相邻线段是否存在交点
    此时 $s_2$ 与相邻线段 $s_3$ 相交，但是 $x_{23}$ 已经存在于队列 $Q$ 中了，所以不用重新加入；
    $s_4$ 与相邻线段 $s_1$ 不相交，转下一步；
    

11. 扫描线扫描到交点 $x_{23}$，从队列 $Q$ 中出队，交换 $L=(s_6,s_5,s_1,s_4,s_2,s_3,s_0)$ 中交点所对应的线段 $s_2,s_4$ 的位置：$L=(s_6,s_5,s_1,s_4,s_3,s_2,s_0)$，重新判断 $s_2,s_3$ 与各自的相邻线段是否存在交点
    此时 $s_2$ 与相邻线段 $s_0$ 相交，但是 $x_{02}$ 已经存在于队列 $Q$ 中了，所以不用重新加入；
    $s_3$ 与相邻线段 $s_1$ 不相交，转下一步；
    

12. 扫描线扫描到末尾端点 $b_1$，从队列 $Q$ 中出队，删除 $L$ 中的 $s_1$，$L=(s_6,s_5,s_4,s_3,s_2,s_0)$，判断与 $s_1$ 相邻的线段 $s_5,s_4$ 是否相交，结果 $s_5$ 与 $s_4$ 相交，将交点 $x_{45}$ 插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
    

13. 扫描线扫描到交点 $x_{02}$，从队列 $Q$ 中出队，交换 $L=(s_6,s_5,s_4,s_3,s_2,s_0)$ 中交点所对应的线段 $s_2,s_0$ 的位置：$L=(s_6,s_5,s_4,s_3,s_0,s_2)$，重新判断 $s_2,s_0$ 与各自的相邻线段是否存在交点
    此时 $s_3$ 与相邻线段 $s_0$ 相交，但是 $x_{03}$ 已经存在于队列 $Q$ 中了，所以不用重新加入；
    

14. 扫描线扫描到交点 $x_{03}$，从队列 $Q$ 中出队，交换 $L=(s_6,s_5,s_4,s_3,s_0,s_2)$ 中交点所对应的线段 $s_0,s_3$ 的位置：$L=(s_6,s_5,s_4,s_0,s_3,s_2)$，重新判断 $s_0,s_3$ 与各自的相邻线段是否存在交点
    此时 $s_3$ 与相邻线段 $s_2$ 相交，但是 $x_{23}$ 已经遍历过了，所以不用重新加入；
    $s_0$ 与相邻线段 $s_4$ 不相交，转下一步；
    

15. 扫描线扫描到交点 $x_{45}$，从队列 $Q$ 中出队，交换 $L=(s_6,s_5,s_4,s_0,s_3,s_2)$） 中交点所对应的线段 $s_4,s_5$ 的位置：$L=(s_6,s_4,s_5,s_0,s_3,s_2)$，重新判断 $s_4,s_5$ 与各自的相邻线段是否存在交点
    结果 $s_4$ 与 $s_6$ 相交，将交点 $x_{46}$ 插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
    $s_5$ 与 $s_0$ 相交，将交点 $x_{05}$ 插入队列 $Q$ 中（按 $y$ 大小排序的位置中）；
    

16. 扫描线扫描到末尾端点 $b_2$，从队列 $Q$ 中出队，删除 $L$ 中的 $s_2$，$L=(s_6,s_4,s_5,s_0,s_3)$，$s_2$ 只与 $s_3$ 相邻，所以不做任何操作；
    

17. 扫描线扫描到末尾端点 $b_3$，从队列 $Q$ 中出队，删除 $L$ 中的 $s_3$，$L=(s_6,s_4,s_5,s_0)$，$s_3$ 只与 $s_0$ 相邻，所以不做任何操作；
    

18. 扫描线扫描到交点 $x_{05}$，从队列 $Q$ 中出队，交换 $L=(s_6,s_4,s_5,s_0)$ 中交点所对应的线段 $s_5,s_0$ 的位置：$L=(s_6,s_4,s_0,s_5)$，重新判断 $s_5,s_0$ 与各自的相邻线段是否存在交点，$s_0$ 与相邻线段 $s_4$ 不相交，转下一步；
    

19. 扫描线扫描到末尾端点 $b_5$，从队列 $Q$ 中出队，删除 $L$ 中的 $s_5$，$L=(s_6,s_4,s_0)$，$s_0$ 与相邻线段 $s_4$ 不相交，转下一步；
    

20. 扫描线扫描到交点 $x_{46}$，从队列 $Q$ 中出队，交换 $L=(s_6,s_4,s_0)$ 中交点所对应的线段 $s_6,s_0$ 的位置：$L=(s_4,s_6,s_0)$，重新判断 $s_6,s_0$ 与各自的相邻线段是否存在交点，$s_0$ 与相邻线段 $s_6$ 不相交，转下一步；
    

21. 扫描线扫描到末尾端点 $b_4$，从队列 $Q$ 中出队，删除 $L$ 中的 $s_4$，$L=(s_6,s_0)$，$s_6$ 与相邻线段 $s_0$ 不相交，转下一步；
    

22. 扫描线扫描到末尾端点 $b_0$，从队列 $Q$ 中出队，删除 $L$ 中的 $s_0$，$L=(s_6)$，不做任何操作
    

23. 扫描线扫描到末尾端点 $b_6$，从队列 $Q$ 中出队，删除 $L$ 中的 $s_6$，$L=()$，结束
    

最后

附上另一个案例的链接，供大家自行学习
https://tildesites.bowdoin.edu/~ltoma/teaching/cs3250-CompGeom/spring16/Lectures/cg-segmintersect.pdf文章来源地址https://uudwc.com/A/6Rbr8