C++动态规划经典案例解析之合并石子

1. 前言

区间类型问题，指求一个数列中某一段区间的值，包括求和、最值等简单或复杂问题。此类问题也适用于动态规划思想。

如前缀和就是极简单的区间问题。如有如下数组：

int nums[]={3,1,7,9,12,78,32,5,10,11,21,32,45,22}

现给定区间信息[3,6]，求区间内所有数字相加结果。即求如下图位置数字之和。

Tips： 区间至少包括 2 个属性，起始端和结束端，求和范围包含左端和右端数字。

直接的解法：

累加数组中 0~6区间的值s1。
累加数组中0~2区间的值s2。
将 s1中的值减去s2中的值。得到最终结果。

如果对任意区间的求解要求较频繁，会存在大量的重复计算。如分别求区间[2,5]和[1,5]之和时，分析可知区间[1,5]结果等于区间[2,5]的结果加上nums[1]的值，或者说区间[2,5]的值等于[1,5]的值减nums[1]。简而言之，只需要求出一个如上两个区间中一个区间的值，另一个区间的值就可得到。

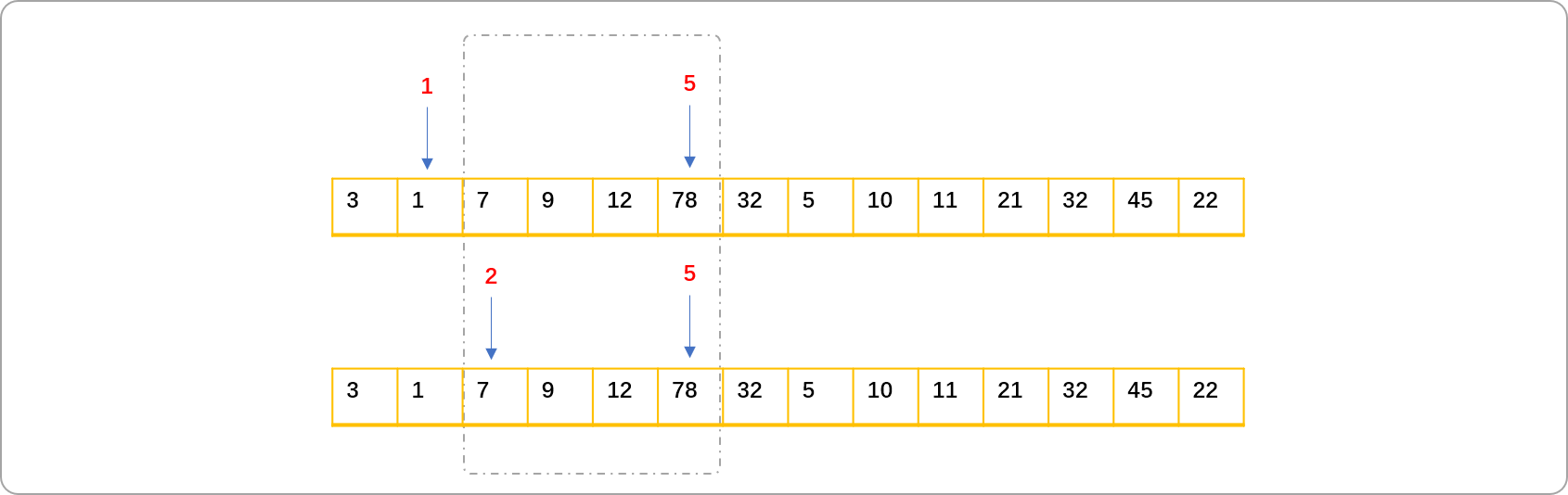
为了减少重复计算，可使用区间缓存理念记录0~至任意位置的和。

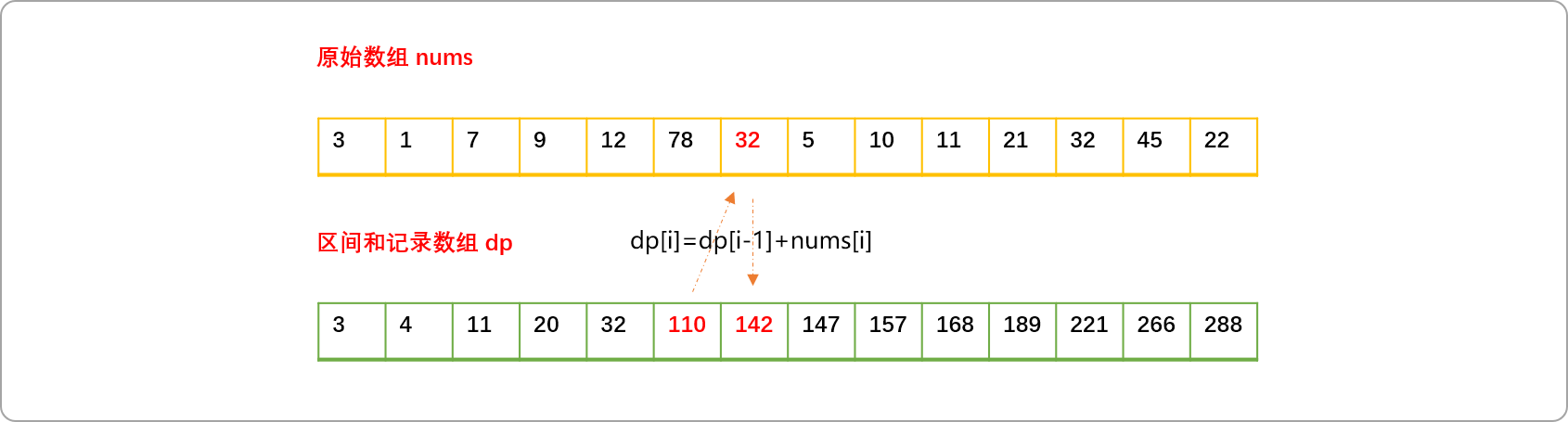
如上的问题便是简单的区间类型问题，解决此类问题的方案称为简单区间类型动态规划。dp数组也可称为前缀和数组。

编码实现：

#include <iostream>
using namespace std;
int main() {
	int nums[]= {3,1,7,9,12,78,32,5,10,11,21,32,45,22};
	int dp[100];
	int size=sizeof(nums)/sizeof(int);
	for(int i=0; i<size; i++) {
		if(i==0){
			//base case 
			dp[i]=nums[i];
		}else{
			dp[i]=dp[i-1]+nums[i];
		}
	}
	//输出dp信息
	for(int i=0; i<size; i++) {
	 cout<<dp[i]<<"\t";
	}

	return 0;
}

有了前缀和数组，计算任意区间数字和的公式为：

//[l,r]：l表示左端位置，r表示右端位置
dp[r]-dp[l-1];

如下代码实现，输入任意区间信息，输出区间和信息。

#include <iostream>
using namespace std;
int main() {
	int nums[]= {3,1,7,9,12,78,32,5,10,11,21,32,45,22};
	int dp[100];
	int size=sizeof(nums)/sizeof(int);
	for(int i=0; i<size; i++) {
		if(i==0) {
			//base case
			dp[i]=nums[i];
		} else {
			dp[i]=dp[i-1]+nums[i];
		}
	}
	//输出dp信息
	for(int i=0; i<size; i++) {
		cout<<dp[i]<<"\t";
	}
	cout<<endl;
	int l,r,sum;
	while(1) {
		cin>>l>>r;
		if(l==-1)break;
		sum=dp[r]-dp[l-1];
		cout<<sum<<endl;
	}
	return 0;
}

前缀和是区间动态规划的极简单应用，下文继续讲解几道典型的区间类型问题。

2. 典型案例

2.1 石子合并

问题描述：

设有N(N<=300)堆石子排成一排，其编号为1,2,3...N，每堆石子有一定的质量m[i] (m[i]<=1000)。现在要将这N堆石子合并成为一堆，每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻。合并时由于选择的顺序不同，合并的总代价也不相同。试找出一种合理的方法，使总的代价最小，并输出最小代价。

此问题为什么也是区间类型问题？

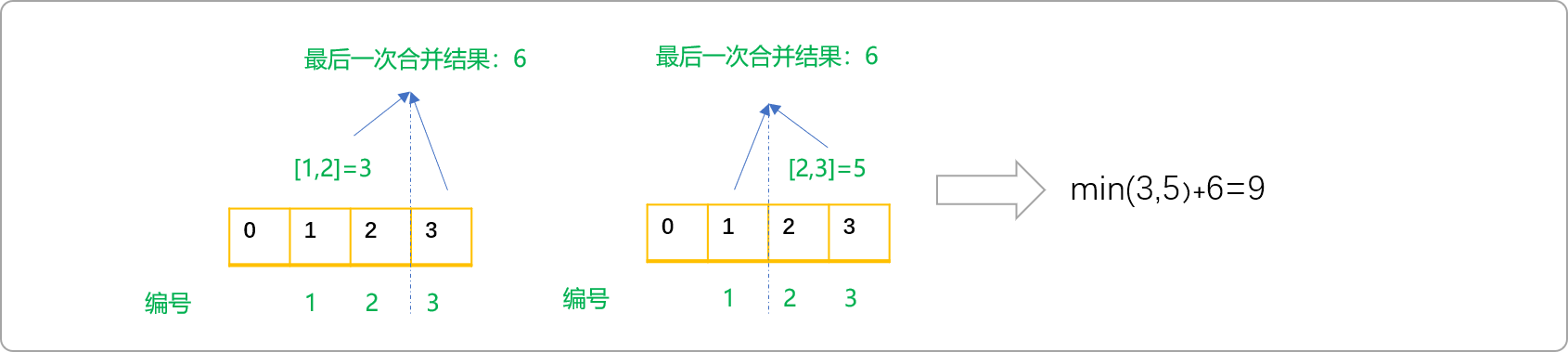
先看几个样例。如有编号为 1,2,3 的 3 堆石子，质量分别为 1,2,3。则合并方案有如下 2 种：

合并编号为1、2的石子，合并代价为3，再合并新堆和第3堆石子，代价为6。总代价为9。
合并编号为2、3的石子，合并代价为5，再合并新堆和第1堆石子，代价为6。总代价为11。

通过上述合并过程，可得到如下有用的结论：

任意相邻两堆石子合并的结果是以这两堆石子的编号作为左、右边界的区间和。如合并编号1,2的石子，代价为区间[1,2]的和。合并编号为2、3的石子，结果为区间[2,3]的和。

无论采用何种合并方案，最后一次合并都是相当于求整个数列的和。

如样例所示，两种合并方案的代价分别为3,5，取最小值3再加上所有石子的质量和6，即为最后答案9。

对于n堆的石子，可以随意在中间画出一条分割线，把n堆石子抽象成左、右2 堆石子（两个区间），根据上述分析，可知最后一次的合并值为这 2堆石子的质量总和。

但是，左堆不是真正意义上只有一堆石子，是由许多石子堆组成的一个逻辑整体，有其内部的合并方案，且不止一种，站在宏观的角度，不用关心其内部如何变化，只需关心多种合并方案的最小值是多少。同理，也只需关心右堆最终返回的最佳值。

所以，求解问题可以抽象成：
```
最终合并最小值=所有石子堆的总质量值+左堆最小合并值+右堆最小合并值
```

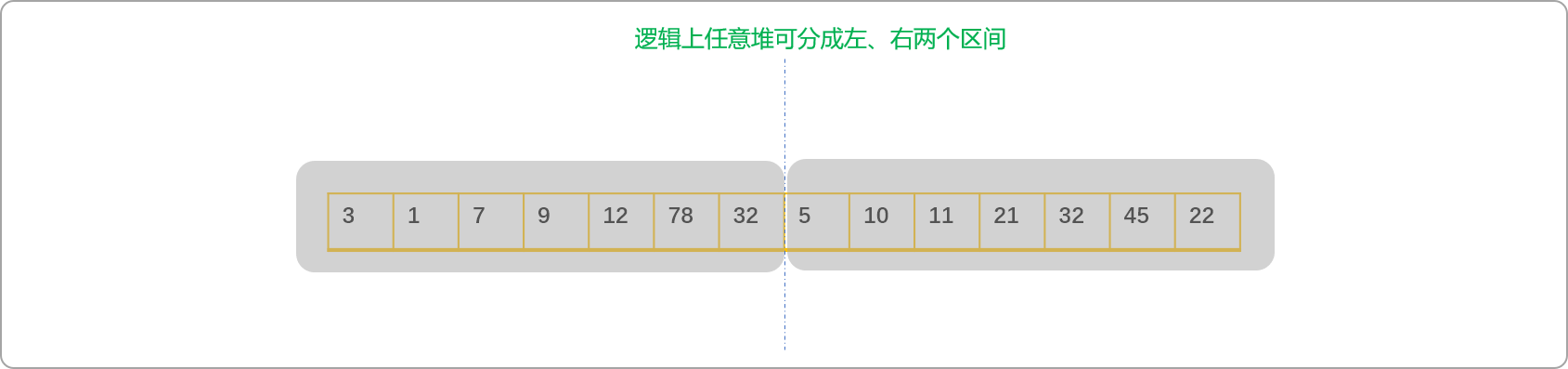
如果原始问题是一个根问题，则求解左堆或右堆的最佳合并值就是一个子问题，所以，合并石子这道题本质是符合递归特点的。

既然符合递归特点，现在就要考虑如何划分子问题。

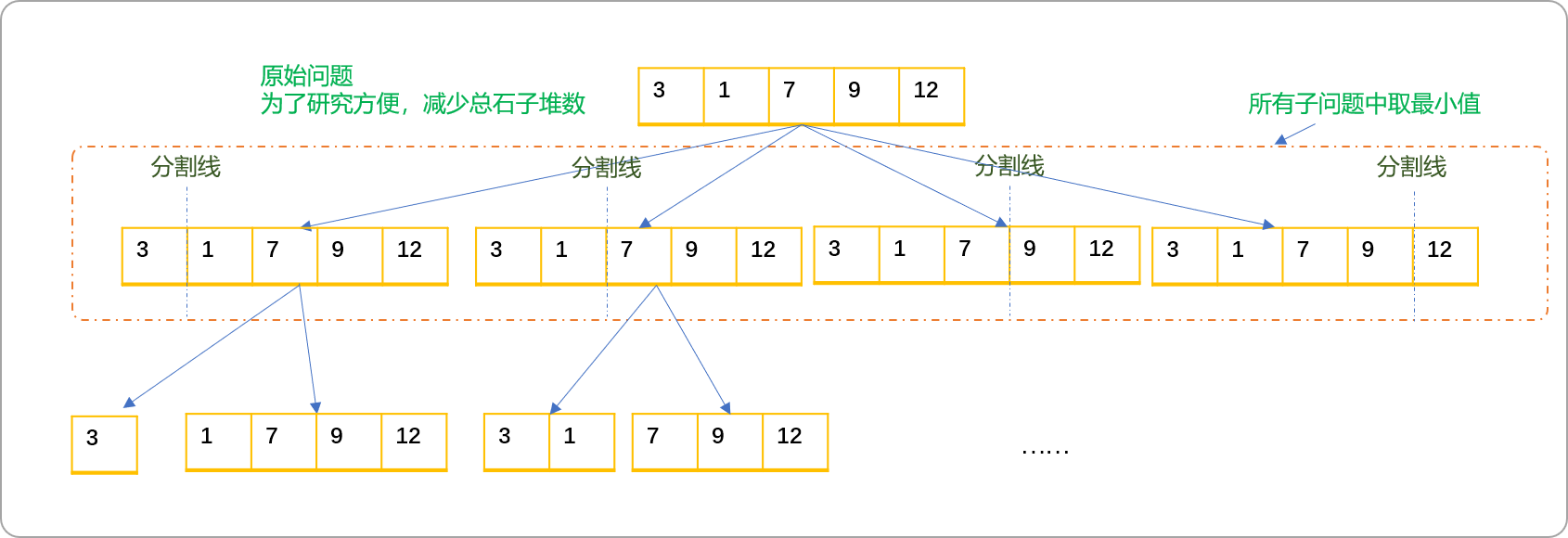
绘制如下图递归树，根问题为原始问题，区间划分可以从第一堆石子开始，然后再移动分割线，最后再在多个子问题返回值中取最小值。

Tips： 如果只有一堆石子，则代价为 0。

编码实现：

初如化变量。

#include <iostream>
#include <cmath>
using namespace std;
//石子质量 
int sz[100]={0};
//石子堆数量
int n; 
//前缀和
int s[100]={0};

初始化石子信息和前缀和。

/*
*  初始化 
*/
void init(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>sz[i];
	}
	//动态规划计算前缀和
	for(int i=1;i<=n;i++){
		s[i]=s[i-1]+sz[i];
	} 
}

递归实现，子问题是一个区间问题，由左、右分界线确定。

int  getSz(int l,int r) {
	//只有一堆石子，返回 0
	if(l==r)return 0;
	int res=1<<30;
	//得到区间的和,最后一次合并值
	int sum=s[r]-s[l-1];
	//计算可分方案，且返回所有分割方案中的最小值
	for(int k=l; k<r; k++) {
		res=min(res,  getSz(l,k)  + getSz(k+1,r) );
	}
    //返回最后一次合并的值加上左、右区间的合并值
	return sum+res;
}

测试。

int main() {
	init();
	int res= getSz(1,n);
	cout<<res;
	return 0;
}

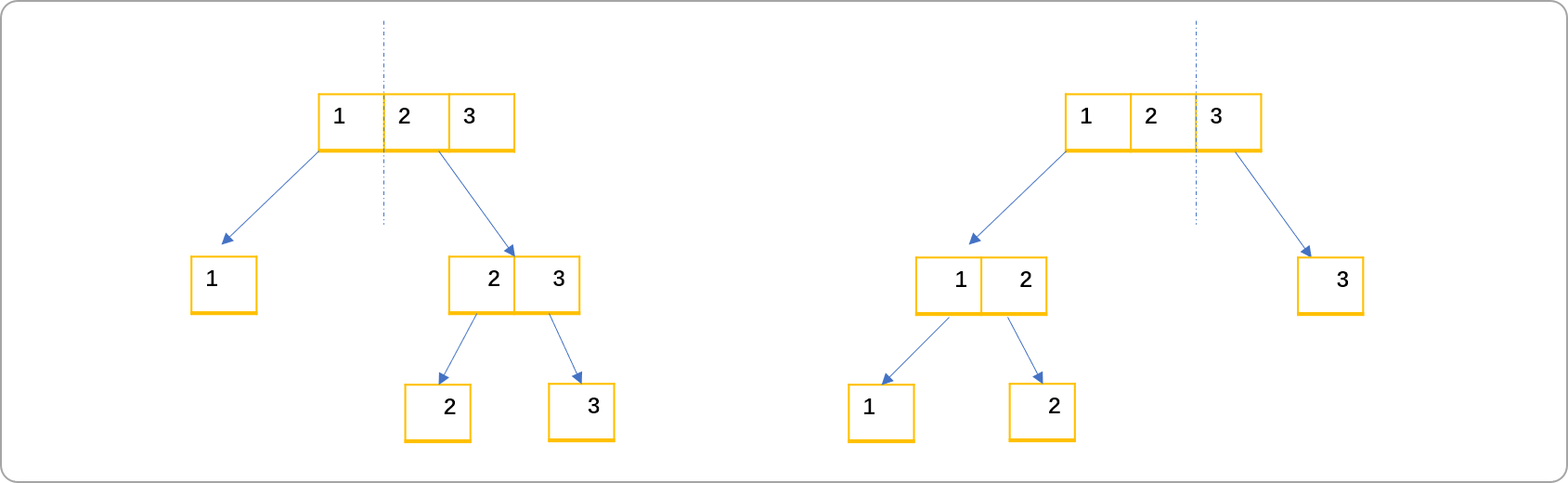
是否存在重叠子问题？

如下图所示，当石子堆更多时，重叠子问题更多。

使用记忆搜索解决重叠子问题。

//记忆数组
int dp[100][100]={0}; 
int  getSz(int l,int r) {
	//只有一堆石子，返回 0
	if(l==r)return 0;
	if(dp[l][r]!=0)return dp[l][r];
	int res=1<<30;
	//得到区间的和,最后一次合并值
	int sum=s[r]-s[l-1];
	//计算可分方案，且返回所有分割方案中的最小值
	for(int k=l; k<r; k++) {
		res=min(res,  getSz(l,k)  + getSz(k+1,r) );
	}
	return dp[l][r]=sum+res;
}

递归是由上向下逐步向子问题求助，类似问题也可以采用由下向上的动态规划方案实现。基本思路，每一次合并过程，先两两合并，再三三合并，…最后N堆合并。

/*
*动态规划
*/
int dpSz() {
	int ans=0;
	//初始化dp 数组
	for (int i = 1; i <= n; i++) {
		for(int j=1; j<=n; j++) {
			dp[i][j]=1<<30;
		}
		//一堆石子的值为 0
		dp[i][i] = 0;
	}
	//从长度为 1 的区间开始扫描，逐步增加区间的长度
	for (int len = 1; len < n; len++)
		//左边界
		for (int i = 1; i < n; i++) {
			//右边界
			int j = i + len;
			//左右之间的所有子区间
			for (int k = i; k < j; k++) {
				dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]);
			}
			ans=max(ans,dp[i][j]);
		}
	return ans;
}

测试：

int main() {
	init();
	int res=dpSz();
	cout<<"动态规划方案："<<res<<endl;
	printf("%d\n", dp[1][n]);
	return 0;
}

2.2 石子合并 II

问题描述：

有 n 堆石子围成一个圈，第 i 堆石子有 a[i] 颗，每次我们可以选择相邻的两堆石子合并，代价是两堆石子数目的和，现在我们要一直合并这些石子，使得最后只剩下一堆石子，问总代价最少是多少?

因为首尾可合并，相比较上述问题，差异在于增加合并的方案。

那么，到底增加了那些合并？

假设石子有 3 堆，每堆的质量分别为 1 2 3。

如果考虑环形问题，则任何数字都可以为头、为尾，则会出现如下几种数列。

1 2 3
2 3 1
3 1 2

可以理解，数列变成如下形式，即将环形变成线性。

动态规划实现：

#include <bits/stdc++.h>
using namespace std;

int n, a[501], f[501][501], s[501];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        a[n + i] = a[i];
    }    
    for (int i = 1; i <= 2 * n; i++)
        s[i] = s[i - 1] + a[i];
    memset(f, 127, sizeof(f));
    for (int i = 1; i <= 2 * n; i++)
        f[i][i] = 0;
    for (int l = 1; l < 2 *n; l++)
        for (int i = 1; i <= 2 * n - l; i++) {
            int j = i + l;
            for (int k = i; k < j; k++)
                f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
        }
    int ans = 1 << 30;
    for (int i = 1; i <= n; i++)
        ans = min(ans, f[i][i + n - 1]);
    printf("%d\n", ans);
}

3. 总结

沉淀过程是一种修行。文章来源地址https://uudwc.com/A/6zqJX