1. 多阈值处理介绍

之前介绍的都是全局单个阈值对图像的分割。固定阈值法，阈值是人工根据灰度直方图的波谷进行设置的。全局阈值法，根据不停的迭代两个区域间的平均灰度进行分割。OUST最大类间方差法，是根据两个子区域不同类之间的最大方差分割。

事实上，OTSU大津法可以扩展到任意数量的阈值

只需要将之前两个类的类间方差更改为三个类即可：

P1是第一个区域的像素概率，及落在第一个区域的像素点 / 总像素点个数
P2 、 P3 是落在第二、第三区域的概率。因此满足 P1+P2+P3 = 1
mG 是整幅图像的平均灰度， m1、m2、m3 是三个区域各自的平均灰度
它们有着下面的关系：

这里只要保证类间方差σB 最大的话，就可以完成三个区域的分割

因为分割三个区域，需要两个阈值k1、k2，因此阈值的范围需要注意

灰度值的范围：

第一区域G1----------------k1-----------------第二区域-----------------k2---------------------第三区域

迭代的过程从k1开始，k1的范围是：1~L-3 ，因为0是没有意义的，灰度值0的前面没有第一区域，同样，如果k1取到最后的两个灰度值的话，就没有k2以及第二第三区域了

然后k2开始迭代，k2的范围是：k1+1~L - 2 ，也是同样的道理，假设L=256的话，k2最多取到254，要不然第三区域也就没有了

注意，这个迭代过程是类似于打印九九乘法表的方式迭代，不能先迭代出k1，在迭代出k2

2. 代码讲解

我们所有的工作就是为了求等号右边的值，然后通过迭代k1、k2，找到最大的类间方差σB

首先，计算全体图像的灰度直方图hist，定义灰度范围grayScale

然后计算出图片像素点的个数，为了求P1、P2、P3 各个区域的像素概率

最后求出mG 整幅图像的平均灰度

然后，开始迭代k1，因为k1的位置就可以确定第一区域G1的像素区域。如下，灰度值小于等于k1的都是第一区域G1的像素点

通过切片，找出G1区域的灰度动态范围和像素点的直方图。

然后计算P1的值和G1区域的平均灰度。这里为了防止G1区域没有像素点做了判断

然后开始迭代k2，大于等于k2的为第三区域。

下面的代码就是计算G3区域的像素概率P3和平均灰度m3

最后就是计算G2区域的值，通过之前P和m对应的关系，可以之间用公式计算得出

然后判断类间方差varB是否是最大的，是的话保存k1、k2、varB到T1、T2、varMax里面。

最后就是多阈值处理，将两个阈值和图像返回即可

3. 完整代码

import cv2
import numpy as np


# 多阈值处理
def double_threshold_processing(x):   # x 为传入的图像
    hist = cv2.calcHist([x], [0], None, [256], [0, 256])  # 图像的灰度直方图  shape = (256,1)
    grayScale = np.arange(256).reshape(1, -1)             # 灰度级 [0,255]  shape =(1,256)
    sum_pixels = x.shape[0] * x.shape[1]                  # 图像总共像素点的个数
    mG = x.mean()                                         # 整幅图像的平均灰度

    T1,T2,varMax = 0,0,0.0        # 双阈值T1、T2，类间方差varMax

    for k1 in range(1,254):     # k1范围在1 - 253之间 1 ~ L-3

        gray_G1 = grayScale[:, :k1 + 1]               # 灰度值 0~k1 的子区域G1
        hist_G1 = hist[:k1 + 1, :]                    # 子区域G1的直方图 0~k1 ,对应每个灰度值的像素点
        sum_gray_G1 = np.dot(gray_G1, hist_G1)        # G1 区域所有像素点灰度值总和 = 灰度值 * 对应像素点的个数
        sum_pixels_G1 = sum(hist_G1)                  # G1 像素数量
        P1 = sum_pixels_G1 / sum_pixels               # G1 像素占比
        m1 = (sum_gray_G1 / sum_pixels_G1) if sum_pixels_G1 > 0 else 0        # G1 像素的平均灰度

        for k2 in range(k1+1,255):     # k2范围在 k1+1 ~ 254 之间 k1+1 ~ L-2
            gray_G3 = grayScale[:,k2:]                # 灰度值 k2~L-1 的子区域G3
            hist_G3 = hist[k2:,:]                     # 子区域G3的直方图 k2~L-1 ,对应每个灰度值的像素点
            sum_gray_G3 = np.dot(gray_G3,hist_G3)     # G3 区域所有像素点灰度值总和 = 灰度值 * 对应像素点的个数
            sum_pixels_G3 = sum(hist_G3)              # G3 像素数量
            P3 = sum_pixels_G3 / sum_pixels           # G3 像素占比
            m3 = (sum_gray_G3 / sum_pixels_G3) if sum_pixels_G3 > 0 else 0        # G3 平均灰度

            P2 = 1.0 - P1 - P3              # G2 区域的像素占比
            m2 = ((mG - P1 * m1 - P3 * m3) / P2) if P2 > 0 else 0   # G2 平均灰度

            varB = P1 * (m1 - mG) ** 2 + P2 * (m2 - mG) ** 2 + P3 * (m3 - mG) ** 2  # 类间方差

            if varB > varMax:        # 保存最大的类间方差
                T1,T2,varMax = k1,k2,varB

    x[x <= T1] = 0
    x[(x>T1)&(x<T2)] = 123  # 中间的灰度，可以更改
    x[x >= T2] = 255

    return T1,T2,x


img = cv2.imread("img.tif",0)
ret1,ret2,dst = double_threshold_processing(img.copy())         # 多阈值处理
print(ret1,ret2)

cv2.imshow('img',np.hstack((img,dst)))
cv2.waitKey()
cv2.destroyAllWindows()

处理的结果：返回的两个阈值为：80 、 178

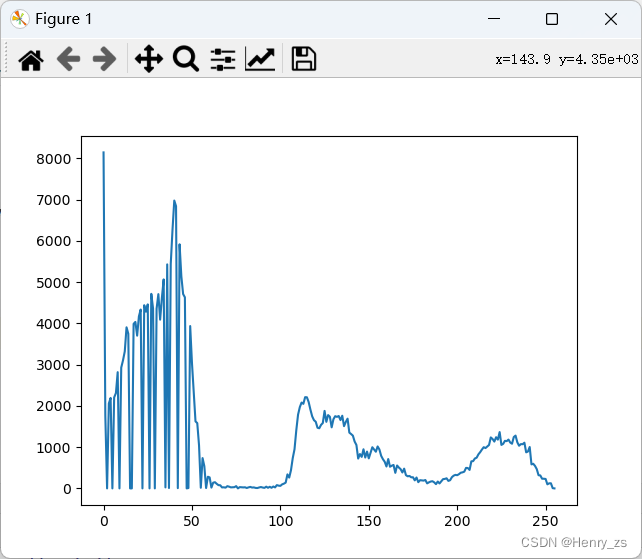
双阈值处理的方法应用于灰度直方图有两个波谷的情况，如下

图像分割 - 阈值处理 - 多阈值处理(OTSU)

1. 多阈值处理介绍

2. 代码讲解

3. 完整代码