最近在阅读框架源码时被旋转矩阵左乘右乘绕的云里雾里,故写下一篇记录一下,以防自己不长记性,转载出处均已标明。此篇没有大段推导,只有结论。
1.左乘是相对固定坐标系,右乘是相对当前坐标系
注意,此时讨论的左乘右乘并非带上点p(x,y,z)的坐标(R*p),仅讨论旋转矩阵相乘顺序(R1*R2*R3(右乘) or R3*R2*R1(左乘))。
对于这句话从文字上理解会很不容易理解,图可以轻松理解。

在外部定义一个坐标系s(可以理解为我们的世界坐标系)。
(1)当上方图片坐标轴b围绕外部坐标系(世界坐标系)即为Rsb'=R*Rsb 相当于左乘一个旋转矩阵,故对应第一句话,左乘是相对固定坐标系。
(2)而下方图片则是绕b(自己)的Z轴旋转时,旋转矩阵为Rsb'=Rsb*R 相当于右乘一个旋转矩阵,故对应第二句话,右乘是相对当前(自己)坐标系。
2.对于上述两句话的理解
(1)对于连续的两次相对于外部坐标系(世界坐标系)的变换,如由IMU坐标系下乘外参旋转矩阵R1(世界坐标系下的矩阵)至Lidar坐标系,再由雷达坐标系下乘一个外参旋转矩阵R2(世界坐标系下的矩阵)转换至Camera坐标系下,那总体旋转矩阵应该是R=R2*R1,由R1向左乘。
(2)对于连续两次相对于自身坐标系的变换,如由IMU位姿1乘旋转矩阵R1(自身)转至IMU位姿2,再由IMU位姿2乘旋转矩阵R2(自身)转换至IMU位姿3,类似下图。那总体旋转矩阵应该是R=R1*R2,由R1向右乘。图来源:旋转矩阵为何左乘是相对固定坐标系,右乘是相对当前坐标系? - 知乎

坐标系内的点p,左乘R代表的是p点在另一坐标系下的坐标,与R(自身位姿姿态)的左右乘并不是一个含义。 得出的R_G_A'既是位姿变换矩阵,也是A'到G的外参。矩阵间变换是右乘,而点坐标变换是左乘。
下面是旋转表示的含义
转自:
旋转的左乘与右乘_无偏估计的博客-CSDN博客_旋转矩阵左乘和右乘
以z轴旋转为例:
第一种物理意义,坐标系的旋转,其应用场景有SLAM,机械臂运动学等。

如上图所示,P点不变,坐标系O-xyz旋转得到O-x'y'z'坐标(可以理解为slam中同一个点在不同帧坐标系下的表示)。新坐标系下,P的坐标变为P',则有:
例如位姿T_lidar * T_lidar_imu = T_imu 意味着由lidar的位姿转到imu的位姿,中间的变换矩阵就是IMU到雷达的外参,如果我们知道imu坐标系下一点P_imu,则其在雷达坐标系下的坐标为
P_lidar=T_lidar_imu*P_imu
第二种物理意义,向量的旋转,其应用场景有机器人的姿态估计等。

如上图所示,坐标系O-XYZ不变,点P'绕Z轴旋转α得到新的点P,则有:
以下转自![]() https://blog.csdn.net/weixin_45632220/article/details/117735223
https://blog.csdn.net/weixin_45632220/article/details/117735223
坐标变换
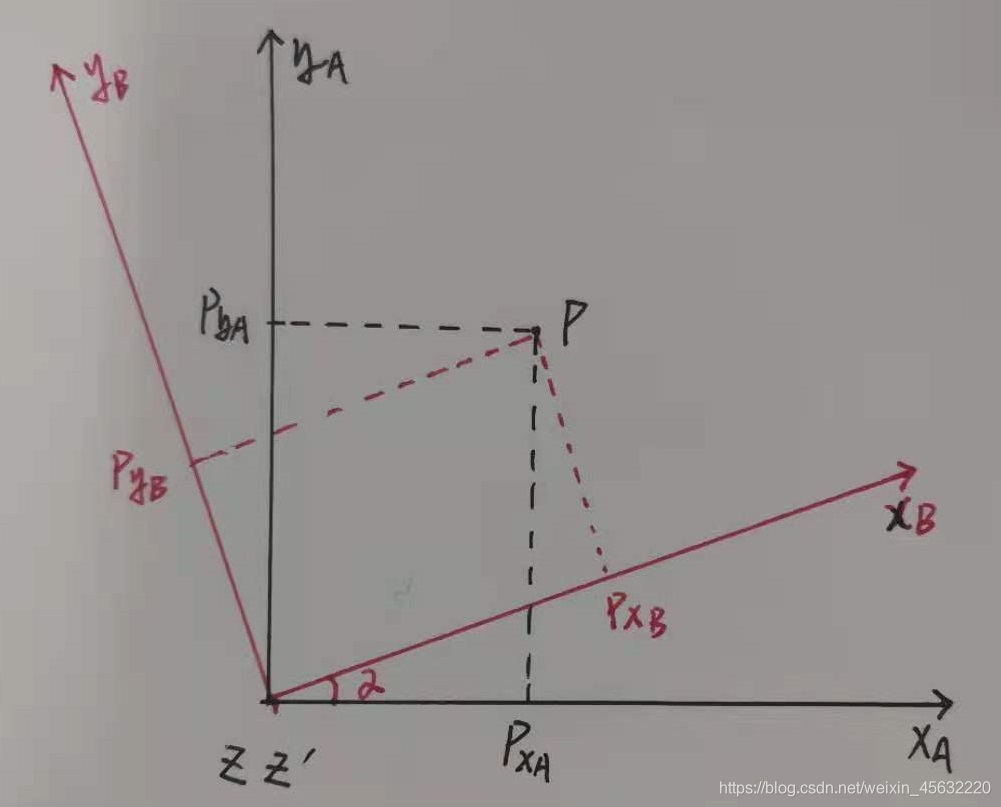
如图所示,对于p点(或者叫向量),可以分别在不同坐标系下表示,红色坐标系绕黑色坐标系旋转了α角度:
其坐标变换关系如下:
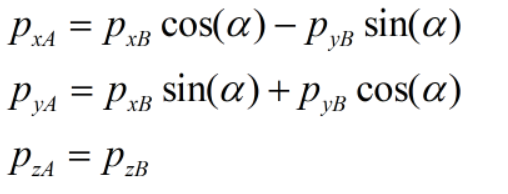
该变换关系由几何关系推导出,具体细节先不管,我们看上式写成矩阵形式是啥样:
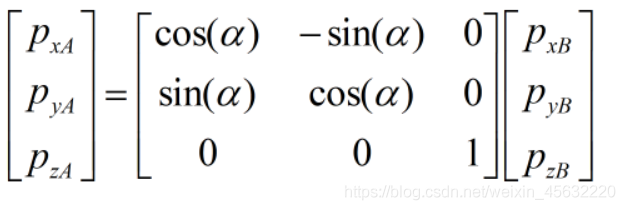
中间的2×2矩阵即为我们所说的旋转矩阵,这里特别要注意,这个矩阵的意义是将p点在旋转后的坐标系(红色)中的坐标,转换为旋转前的坐标系(黑色)中的坐标。(即求出1到2的位姿变换,可以将2中的点的坐标左乘此位姿变换得到在坐标系1中的点坐标)文章来源:https://uudwc.com/A/9j3O
从黑色位姿到红色位姿的变换矩阵为R,已知P在红色位姿中的坐标为Ph,则在黑色(原始坐标)中的坐标为Pb=R*Ph
文章来源地址https://uudwc.com/A/9j3O
