论文阅读 - Outlier detection in social networks leveraging community structure

摘要

1. Introduction

2. Related works

3. Preliminaries

3.1. 模块化度量

3.2. Classes of outliers

3.2.1. 点异常

3.2.2. Contextual anomalies

3.2.3. Collective anomalies

3.3. Problem definition

3.4. Outliers score

4. Methodology

4.1. Proposed approach

4.2. Complexity analysis

4.3. Implementation

文章来源地址https://uudwc.com/A/AA6zE

摘要

社交网络已成为现代社会的一个重要方面，并逐渐成为世界范围内不可或缺的交流手段。每天都有大量数据通过社交网络传输。因此，确保安全成为一种必要。可疑用户或垃圾邮件发送者可能会对用户在网络上共享的信息和数据构成威胁。有鉴于此，异常值检测是网络通信的一个重要方面。本文提出了一种新技术，利用网络社区结构从全局角度识别网络中的异常情况。一般来说，最先进的异常值检测算法主要关注单个节点及其直接邻域。但我们的技术只考虑那些倾向于属于多个社区的节点，或其邻居属于同一社区或不属于任何社区的节点。

在合成网络和真实世界网络上的实验结果表明，与最先进的算法相比，我们的 F-Score 和 Jaccard 相似度分别提高了 7-10% 和 29%。此外，与最先进的算法相比，我们的计算速度提高了近 1.83 倍。

1. Introduction

在过去的几十年里，社交网络（SN）已成为全球用户之间交流的重要媒介，用户之间共享着大量的数据和信息。如今，Facebook、Twitter 等社交网络拥有数十亿用户。对这些用户进行验证变得极为重要，因为他们可能对网络上共享的信息构成威胁，并可能导致盗窃、欺诈、有组织犯罪甚至恐怖活动[1]。因此，识别社交网络中的可疑用户最近引起了广泛关注。

一般来说，社交网络包含社区[2]，在这些社区中，用户形成了联系紧密的子群，因此子群之间的联系与同一子群内部的联系相比是稀疏的[3,4]。社交网络中的离群值被定义为往往属于一个以上社群的用户，或其邻居只属于一个社群或不属于任何社群的用户[5]。迄今为止，已有多项研究识别出了社交网络中的离群值 [6-10]，但其中大多数研究的速度较慢，且计算量较大。

本文展示了一种利用网络社区结构快速查找社交网络中异常值的方法。通过只关注最有可能成为离群值的挂点节点和社区边界节点（CBN）1，搜索空间被大大缩小。然后，我们使用一种称为 "永久性"（permanence）的基于节点的指标来评估 CBN 在其社区内的关联性 [11]。

本文的主要贡献如下：

利用 SN 的社群结构来识别离群值，其中社群边界节点使用基于节点的度量标准 "永久性"（permanence）[11]来处理，这是我们所知的首个研究。

在合成网络和真实世界网络上进行的实验评估结果表明，与现有作品相比，F- Score 和 Jaccard 相似度分别提高了 10%和 29%。此外，与最先进的算法相比，所提出的技术实现了 1.83 倍的提速。

我们将本文的其余部分安排如下。第 2 节介绍了相关工作。第 3 节正式定义了问题陈述和衡量标准。第 4 节的目的是说明如何利用群落结构来识别异常值。第 5 节介绍了实验结果。在第 6 节中，我们对结果进行了分析。最后，我们将在第 7 节中结束本文。

2. Related works

在过去几年中，研究人员对社交网络中的异常值检测问题进行了广泛的研究。

Keyvanpour 等人在 [2] 中提出了一种基于网络社区结构的方法来识别社交网络中的异常点。该方法没有通过应用额外的特征或特征组合方法来提高异常评分。这种方法只适用于静态图，而社交网络是随时间变化的。

Win 等人在文献[9]中提出了一种基于边缘结构的社交网络社区检测方法，利用节点的相似性进行邻域重叠，从而识别异常值。

Gupta 等人在文献[7]中提出了一种基于异构信息网络中社区分布的异常值检测技术，如果节点的异常值偏离了常见的社区分布模式，就会被识别出来。实验评估表明，该算法能够检测出不同程度的离群值、数据维度和多种类型的离群值。该算法没有考虑流场景中涉及多个时间网络快照的情况。

Helling 等人在 [10] 中提出从全局角度找出异常节点。如果一个节点属于一个社区，但却连接到多个不同的社区，那么这个节点就是异常节点。该算法与某些边呈线性扩展，比以前的工作有所改进。本文重点介绍了用于社区检测的 CADA 算法，但还需要进行比较研究，以确定哪种社区检测方法对节点异常检测最稳健。

Pandhre 等人在 [12] 中提出了一种基于图的节点和边数据的新型离群节点检测方法。

Berenhaut 等人在 [13] 中提供了一种从诱导局部比较中获得图结构信息的方法。该方法的不足之处在于，天真算法的实现需要花费立方时间。目前，该方法适用于最大规模为 20,000 的数据集。

Anand 等人在他们的研究成果[14]中概述了现有的社交网络异常检测技术，分为基于结构的方法和基于行为的方法。

在 [15] 中，作者使用了一种基于距离度量的离群点检测方法来检测在线社交网络（OSN）中的潜在谣言。

Khamparia 等人在 [16] 中提出了一种结构化多层次系统，用于对不同在线社交网络（OSN）中的异常情况进行分类。该算法还有待在许多数据集上进行测试，并应通过大型实时数据集进行验证。

Aggarwal 等人在 [17] 中研究了许多小型图中的离群点检测问题，调查了从全局角度检测离群点的各种可用模型，并对图中局部和全局结构的显著变化（通常是突变）进行了研究。尽管迄今为止已有许多文献报道了离群值检测方法，但其中大多数都需要大量的计算且速度较慢。

在本文中，我们利用 SN 的群落结构来识别离群值，通过只处理垂点和群落边界节点，显著减少了搜索空间。与其他最先进的算法相比，本文提出的技术总能更好地识别离群值。

3. Preliminaries

让我们考虑一个社交网络G（V ,E ），网络中的每个用户都表示为节点 $v_i \in V$ ，用户之间的关系表示为边 $(v_i,v_j) \in E$ 。在社交网络中，社群结构意味着节点被自然划分为子群 $C = \{c_1,c_2,...,c_k\}$ ，因此同一子群内的用户之间存在密集的联系。相反，子群之间的联系相对稀疏 [18] 。

定义 1. 设 $C = \{c_1,c_2,...,c_k\}$ 是网络G（V , E）的一个社区结构。如果对于任意两个社区 $c_i,c_j$ 且在 , $c_i \cup c_j = \oslash$ ，其中 i≠j [19]，则称其为无连接社区。

例 1. 对于一个给定为G (V , E) 的网络，图 1 显示了将 G 分解成不同社区的可能方案。

定义 2. 给定网络G ( V,E ) 的互不相交群落结构，具有群落间边的节点称为群落边界节点 (CBN) [18] 。

例 2. 分解成不相交群落结构的情况如图 1 所示，集合为 CBN = {3, 4, 6}

3.1. 模块化度量

为了量化脱节群落结构的质量，我们使用了广受认可的模块化度量 Q [20]，其数学表达式为

其中 $|E_c|$ 表示特定社区c内所有边的总计数， $|k_c|$ 表示社区c内所有节点的度数总和，即 $kc = \sum_{v \in c}d_v$ ，其中 $d_v$ 是节点的度数。

根据定义，0 ≤ Q ≤ 1，该值越接近统一值，表示群落结构质量越好，即群落内部的联系比群落之间的联系密集。

3.2. Classes of outliers

所需的异常类别是异常值检测技术的关键要素。异常值分为以下三类：

3.2.1. 点异常

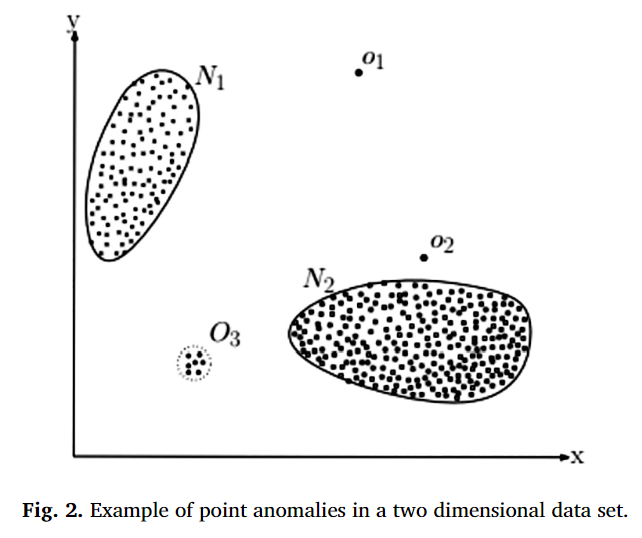
如果一个数据实例与其他数据相比可以证明是异常的，那么它就被称为点异常[21]。大多数异常检测研究都以这种异常为中心，因为从概念上讲，它是最简单的异常。例如，在图 2 中，数据点 o1、o2 和图 1 中区域 O3 中的数据点都位于被认为具有正常数据点（N1 和 N2）的区域边界之外，因此属于点异常。现实生活中的一个例子是入侵检测。让数据集代表来自单个系统的广播。为简单起见，假设数据只包含一个属性：广播频率。假设与给定时间内广播频率的典型范围相比，任何软件包的播出时间都很短。在这种情况下，这可能会被视为全局异常值，我们可以推断相关系统可能已被入侵。

3.2.2. Contextual anomalies

上下文异常或条件异常是指数据实例在特定上下文中并不常见（但在其他地方并不常见）。数据集的结构意味着上下文的概念，而上下文必须作为问题表述的一部分加以说明。每个数据实例都使用两组上下文属性和行为属性来定义。上下文属性决定了实例的上下文或邻域（如空间数据集的经度和纬度）。行为属性决定了每个数据实例的非上下文特征（例如，对于描述全球平均降雨量的空间数据集，任何地区的降雨量）[21]。以信用卡欺诈检测为例。在信用卡领域，购买时间是一个上下文属性。假设一个人每周的购物支出平均为 1000 卢比，只有圣诞节那一周会飙升至 10,000 卢比。在八月的一个星期内新购买 10,000 卢比将被视为背景异常，因为它偏离了该人在当时背景下的惯常行为（尽管在圣诞节周内的相同消费金额将被视为正常）。

3.2.3. Collective anomalies

如果相关数据实例的集合对整个数据集而言是偏心的，则称为集体异常。图 3 展示了人体心电图输出的一个示例 [22]。由于同一低值持续时间过长，图中突出显示的区域表示异常（对应于心房早搏），尽管低值一般不被视为异常。

3.3. Problem definition

对于已知社区结构的给定社交网络G（V ， E），目标是识别离群节点集 $V_o$ ∈ V。确定的离群节点集属于一个以上的社群，或其邻居只属于一个社群，或不属于任何社群。

3.4. Outliers score

在这项工作中，使用的离群值评分是基于一个节点的指标，称为永久性 [11]，它提供了一个节点在多大程度上属于其社区的定量指标，数学定义为

其中 v表示一个节点，每个 $e_i$ ，1 ≤i ≤ k，表示属于第 i 个外部组的邻居数，如果节点没有外部邻居，我们假设e = 1， $d_v$ 表示节点的度， $EN_v$ 表示节点的外部邻居， $IN_v$ 表示节点的内部邻居。

一般情况下，0 ≤ $S_v$ ≤ 1， $S_v$ 值越小，表示节点倾向于属于多个社区，即在其社区内联系松散。而 $S_v$ = 1 则表示节点与其社区的联系紧密。

让我们考虑一个简单的社交网络，该网络由 14 个节点和 26 个连接组成，已知离群结构C = {c1, c2, c3}，如图 4 所示。在图 4 中，节点 5 的离群值计算公式为

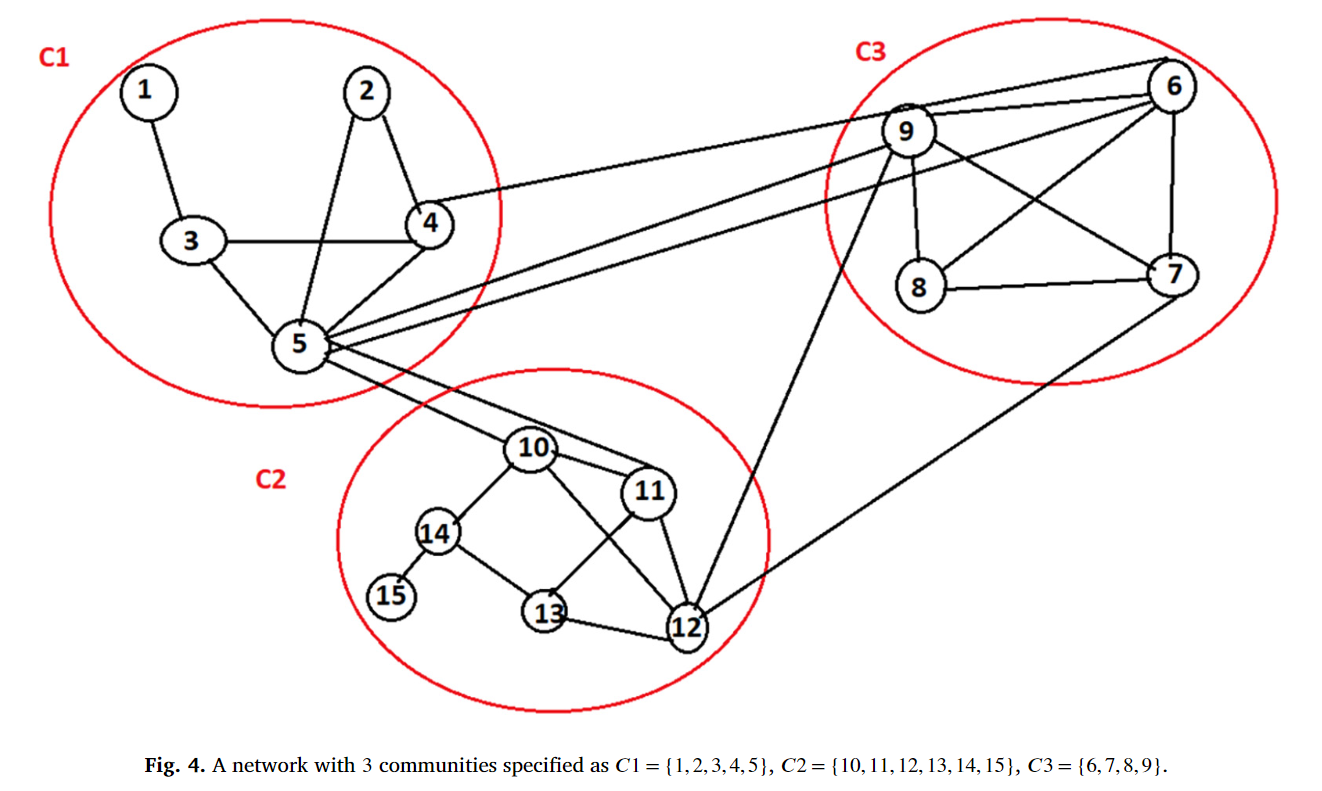
其中，D5 = 7、IN5 = 3、EN5 = 4 和 ENG 5 = {2，2}，即 C2 和 C3 中的两个外部邻居。同样，我们计算其他边界节点的值如下。

4. Methodology

4.1. Proposed approach

迄今为止，已有多种基于社区的技术被提出来检测社交网络中的异常值，但这些技术的计算密集度高、速度慢。在 [10] 中，作者提出了从全局角度发现异常节点的方法，即把与许多其他社区有社区成员链接的节点视为异常节点。利用网络的底层拓扑结构，为网络中的每个节点计算异常得分，异常得分越高，表明节点偏离预期位置或分布的程度越高。

现在，根据我们的工作中对节点离群值的猜想，如果一个节点与其社区成员的联系很弱，并且在其他社区有邻居，那么它很有可能是一个离群值。由于节点有可能在不同的社区中有邻居，因此只需查看位于社区边界的节点就能发现离群值，从而降低了计算成本。

在提议的算法中，我们考虑了两类节点来检测异常值。属于单一社区的节点在其社区内的关联性很弱（如挂节点）。节点与自己的社区联系松散，但与许多其他社区有联系。在此基础上，为每个 CBN 计算基于节点的度量--永久性[11]。永久度从数量上说明了这些边界节点在社区中的成员程度，也就是说，它确定了边界节点对其社区的归属程度[23]。然后，我们使用公式 (2) 计算每个节点的永久性值，如果任何节点S≤ $\beta$ ，则该节点为离群值，其中阈值为 $\beta$ 。对于吊坠节点，很明显它们在其社区内的关联性很弱。因此，我们不对它们进行计算。我们可以通过节点的度数轻松识别它们。算法 1 简要介绍了这一过程。为了更好地利用内存，我们使用了压缩解析行（Compressed-Sparse-Row，CSR）[24] 表示法。

4.2. Complexity analysis

由于网络是天然稀疏的，因此建议的技术需要 O(|V| + |E|) 的空间复杂度，一般来说，|E| ∼ (O|V|)。在计算方面，建议的技术在O (| V|) 时间内识别出挂接节点，计算也需要 (||. )， $d_{max}$ 其中表示节点可能具有的最高度数。

在建议的算法中，|CBNs| ≪ |V | |，而对于大多数真实世界的网络，|E| ∼ O(| V |)，建议的算法具有线性时间复杂度。

4.3. Implementation

我们的算法是用 C 语言在配备 8 GB 内存和 Linux 操作系统的 64 位机器上实现的。我们使用了 Louvain [25] 和 GN [26] 算法进行社区检测。此外，我们还通过实验将阈值设为 0.25。在程序中，我们使用 CSR（压缩稀疏行）表示法[27]来表示一个社交网络（见图 5）。

其中一个数组，即 eptr，用于保存网络中的每一条边，而另一个数组 vptr 则用于获取节点的第一个邻居。以节点 n 为例，如果 n 不是最后一个节点，则 n 的邻居数计算公式为 vptr[n+1]-vptr[n]。否则，我们的计算公式为（2*图中的边数-vptr[n]），耗时为 O(1)。对于相关的社交网络，我们考虑使用 1 到 n 的 ﬂag 数组，其中每个索引代表一个节点及其相应的 ﬂag 值。ﬂag 值分别为 0、1 和 2。ﬂag 值为 1 代表节点度为 1 或只有一个邻居的节点。现在，我们使用公式 (2) 计算 ﬂag 值为 2 的节点的永久性值，该公式定量描述了节点在多个社区中的成员资格程度。如果 ﬂag 值小于或等于阈值，则该节点将与那些 ﬂag 值为 1 的节点一起被归类为离群节点。