Hello算法——笔记

参考资料

1 引言

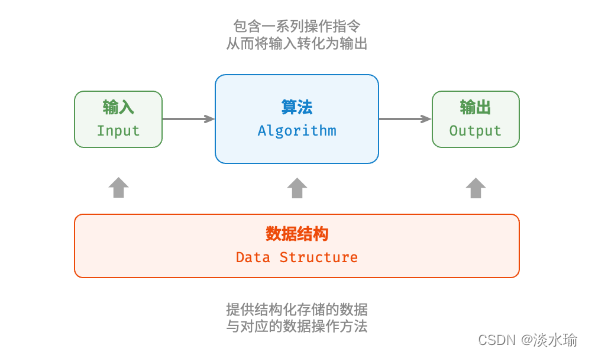
算法

算法是一组用于解决特定问题或执行特定任务的明确定义的计算步骤或指令集合。算法可以被视为一种解决问题的方法或策略，它描述了如何将输入转换为输出，通过一系列的逻辑和数学操作来实现预期的结果。

算法可以用来解决各种不同的问题，例如排序数据、搜索元素、图形处理、数据压缩、机器学习等。它们是计算机科学和计算机编程的核心概念。

良好的算法通常具有以下特点：

• 正确性：算法应该能够产生正确的输出，解决给定的问题。
• 效率：算法应该能够在合理的时间内完成任务，避免不必要的计算和资源消耗。
• 可读性：算法应该易于理解和阅读，便于他人理解和维护。
• 可扩展性：算法应该能够处理不同规模和复杂度的问题，并且在输入规模增加时仍保持良好的性能。

算法的设计和分析是计算机科学的重要研究领域，有许多经典的算法被广泛应用于各种领域。常见的算法设计方法包括贪婪算法、分治算法、动态规划、回溯法、图算法等。算法的复杂性分析涉及时间复杂度、空间复杂度、最坏情况复杂度等概念，用于评估算法的效率和可行性。

总之，算法是计算机科学中非常重要的概念，它们是解决问题和执行任务的基础工具，对于计算机程序的设计和优化起着关键作用。

数据结构

数据结构是一种组织和存储数据的方式，旨在使数据的访问和操作更加高效。它定义了一种数据元素之间的关系，并提供了对这些元素进行插入、删除、查找和修改的操作。

常见的数据结构包括：

• 数组（Array）：将相同类型的数据元素按照一定的顺序存储在连续的内存空间中。
• 链表（Linked List）：通过指针将不同类型的数据元素连接起来，每个元素包含一个指向下一个元素的引用。
• 栈（Stack）：一种先进后出（LIFO）的数据结构，只允许在栈顶进行插入和删除操作。
• 队列（Queue）：一种先进先出（FIFO）的数据结构，允许在队尾进行插入操作，在队头进行删除操作。
• 树（Tree）：一种由节点组成的层次结构，每个节点可以有多个子节点。
• 图（Graph）：由节点和节点之间的边组成的数据结构，用于表示各种实体之间的关系。
• 堆（Heap）：一种特殊的树结构，具有最大堆和最小堆两种形式，用于高效地获取最大或最小元素。
• 散列表（Hash Table）：根据关键字直接访问数据的数据结构，通过哈希函数将关键字映射到存储位置。

数据结构的选择取决于问题的性质和需求。不同的数据结构在空间占用、时间复杂度和操作效率等方面有所不同，合理选择和使用数据结构可以提高程序的性能和效率。

数据结构和算法是计算机科学的核心内容，它们相互依赖，共同构建了计算机程序的基础。理解和掌握不同的数据结构对于解决复杂的计算问题和设计高效的程序非常重要。

算法和数据结构的关系

算法依赖于数据结构来实现具体的操作和计算，而数据结构提供了算法所需的存储和组织数据的方式。良好的数据结构选择和设计可以提供更好的算法效率和性能。
因此，算法和数据结构是相辅相成的，它们共同构建了计算机科学中的基础。深入理解和掌握数据结构和算法对于设计和开发高效的计算机程序至关重要。

2 复杂度分析

算法效率评估，方法：
时间效率：算法运行速度的快慢。
空间效率：算法占用内存空间的大小。

我们的目标是设计“既快又省”的数据结构与算法。

时间复杂度

时间复杂度是一种衡量算法运行时间随输入规模增长的增长率。它表示算法执行所需的时间与输入规模之间的关系。常见的时间复杂度表示方法包括大O表示法，用于描述最坏情况下的运行时间。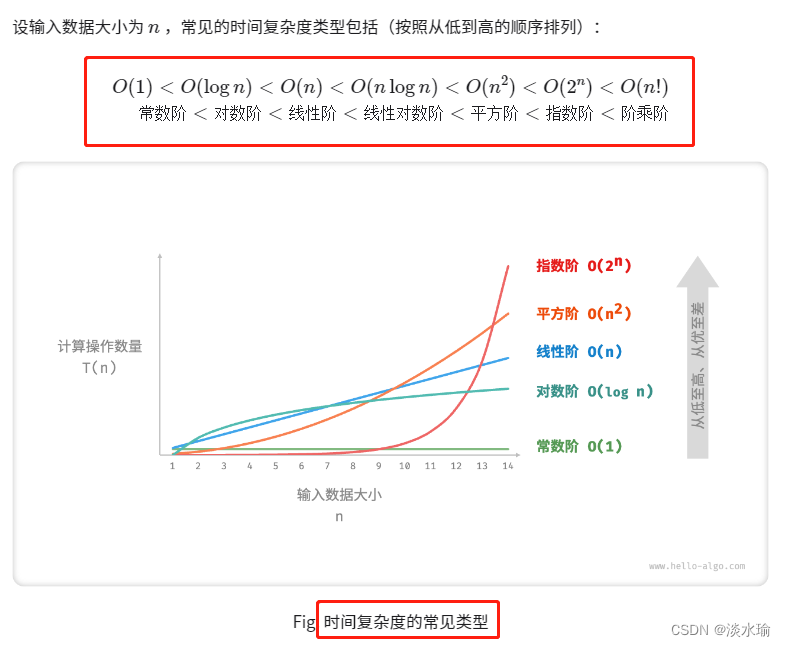

「平均时间复杂度」可以体现算法在随机输入数据下的运行效率。

在进行时间复杂度分析时，我们通常关注最坏情况下的时间复杂度，因为它提供了算法在最不利情况下的性能保证。同时，还可以考虑平均情况下的时间复杂度和最好情况下的时间复杂度。

空间复杂度

空间复杂度是一种衡量算法所需的额外空间随输入规模增长的增长率。它表示算法执行所需的额外空间与输入规模之间的关系。与时间复杂度类似，常见的空间复杂度表示方法也使用大O表示法。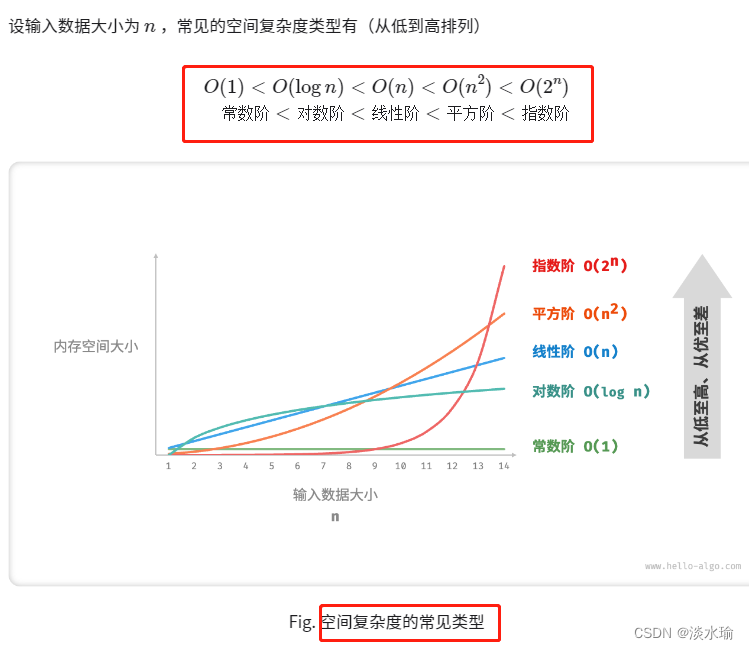

降低时间复杂度通常需要以提升空间复杂度为代价，反之亦然。我们将牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”；反之，则称为“以时间换空间”。

选择哪种思路取决于我们更看重哪个方面。在大多数情况下，时间比空间更宝贵，因此以空间换时间通常是更常用的策略。当然，在数据量很大的情况下，控制空间复杂度也是非常重要的。

3 数据结构

数据与内存

基本数据类型：
数据是指以某种形式或格式表示的信息。在计算机科学和数据结构领域，数据通常是由位（0和1）组成的二进制序列。数据可以包括数字、文字、图像、音频、视频等各种形式的信息。

在计算机科学中，数据可以被组织成不同的数据结构，如数组、链表、栈、队列、树、图等。不同的数据结构适用于不同的场景和问题，可以提供高效的数据存储和访问方式。

「基本数据类型」是 CPU 可以直接进行运算的类型，在算法中直接被使用。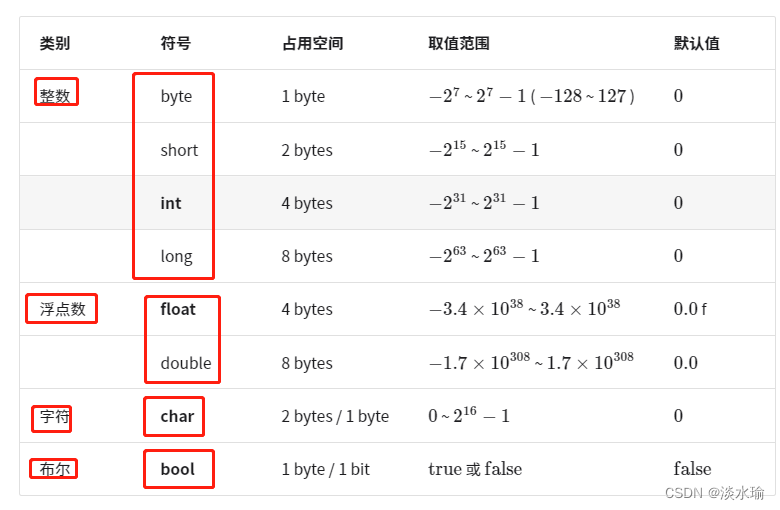

浮点数可以进行各种数学运算，包括加法、减法、乘法、除法等。然而，由于浮点数的内部表示是有限的，存在舍入误差和精度损失的问题。在比较浮点数时，应使用适当的容差值而不是直接进行相等性比较。

计算机内存：
在算法运行过程中，相关数据都存储在内存中。
在数据结构与算法的设计中，内存资源是一个重要的考虑因素。

数据结构分类

1.== 线性数据结构==：线性数据结构中的元素按照线性顺序排列，每个元素只有一个前驱和一个后继。常见的线性数据结构包括数组、链表、栈和队列。
2. 树形数据结构：树形数据结构中的元素以树的形式进行组织，每个元素可以有多个子节点。常见的树形数据结构包括二叉树、堆、平衡树（如AVL树和红黑树）等。
3. 图形数据结构：图形数据结构中的元素以节点和边的形式进行组织，节点表示元素，边表示元素之间的关系。图可以是有向的或无向的，可以有权重或不带权重。常见的图形数据结构包括有向图、无向图、加权图等。
4. 散列数据结构：散列数据结构使用散列函数将元素映射到存储位置，通过关键字快速访问元素。常见的散列数据结构包括哈希表。
5. 字符串数据结构：字符串数据结构用于存储和操作字符串，常见的字符串数据结构包括字符串数组、字符串链表和字典树（Trie）等。

这只是数据结构的一些常见分类方式，实际上还有其他的分类方式。根据具体的应用场景和问题需求，选择合适的数据结构可以提高算法的效率和性能。

根据逻辑结构分类：线性和非线性
逻辑结构：揭示了数据元素之间的逻辑关系。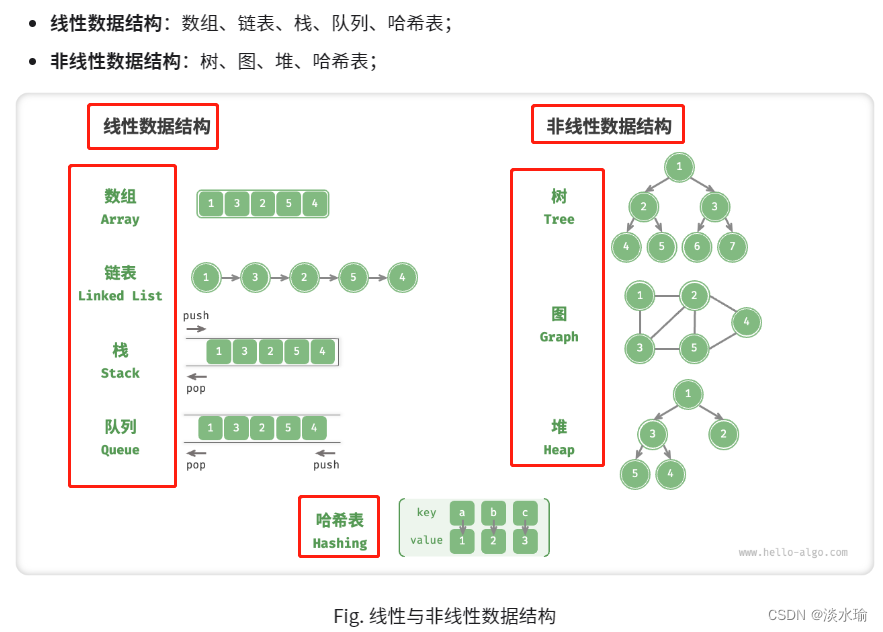

根据物理结构分类：连续和离散
物理结构：体现了数据在计算机内存中的存储方式。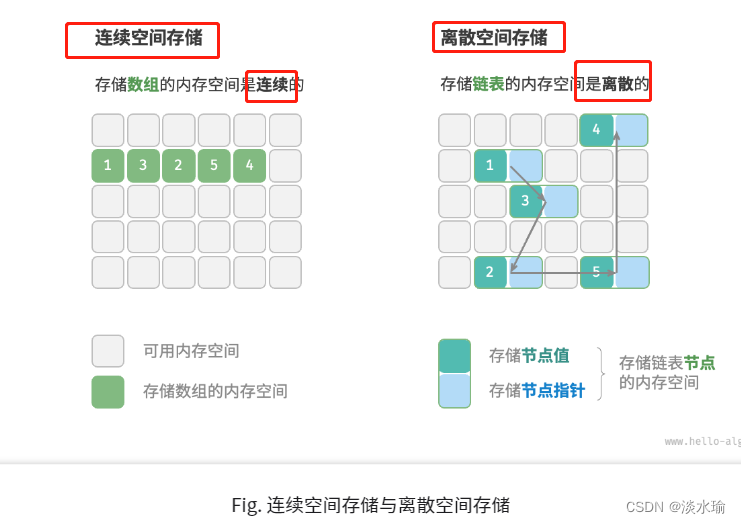

4 数组与链表

数组

「数组 Array」是一种线性数据结构，其将相同类型元素存储在连续的内存空间中。我们将元素在数组中的位置称为元素的「索引 Index」。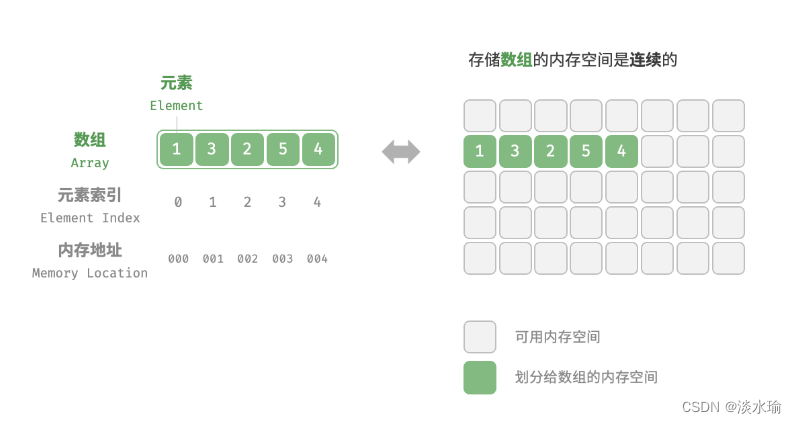

优点：
在数组中访问元素非常高效，索引本质上表示的是内存地址的偏移量。

缺点：
数组中插入或删除元素效率低下。

1. 时间复杂度高：数组的插入和删除的平均时间复杂度均为 O(n)，其中 n为数组长度。
2. 丢失元素：由于数组的长度不可变，因此在插入元素后，超出数组长度范围的元素会丢失。
3. 内存浪费：我们可以初始化一个比较长的数组，只用前面一部分，这样在插入数据时，丢失的末尾元素都是我们不关心的，但这样做同时也会造成内存空间的浪费。

js中基本使用：

1. 创建数组：

使用数组字面量表示法：let array = [value1, value2, ...];
使用new关键字和Array构造函数：let array = new Array(value1, value2, ...);

2. 访问数组元素：

使用索引访问数组元素：array[index]，其中index为元素的索引，从0开始。

3. 修改数组元素：

直接通过索引赋值：array[index] = value，将指定索引处的元素修改为新的值。

4. 获取数组长度：

使用length属性：array.length，返回数组中元素的数量。

5. 添加元素到数组：

使用push方法：array.push(value1, value2, ...)，将一个或多个元素添加到数组末尾。
使用索引赋值：array[index] = value，将元素添加到指定索引处。

6. 删除数组元素：

使用pop方法：array.pop()，删除数组末尾的元素，并返回被删除的元素。
使用shift方法：array.shift()，删除数组开头的元素，并返回被删除的元素。
使用splice方法：array.splice(index, count)，从指定索引处开始删除指定数量的元素。

7. 迭代数组：

// for遍历
for (let i = 0; i < array.length; i++) {
  // 访问 array[i]，进行相应操作
}

// forEach遍历
array.forEach(function(element) {
  // 对每个元素执行操作
});

链表

定义：
链表（Linked List）是一种常见的数据结构，用于存储和组织数据。与数组不同，链表的元素不是按照索引来访问，而是通过链接（指针）连接起来的。
链表由一系列节点（Node）组成，每个节点包含两个部分：数据域和指针域。

由于指针记录了下个节点的内存地址，因此无需保证内存地址的连续性，从而可以将各个节点分散存储在内存各处。

优点：
链表中插入与删除节点的操作效率高。

1. 动态大小：链表的长度可以根据需要动态增长或缩小，不像数组长度固定。
2. 灵活插入和删除：在链表中插入和删除元素的操作相对容易，只需要调整指针的指向即可，不需要像数组一样进行元素的搬移。
3. 顺序访问：链表的元素只能按照顺序访问，而不能随机访问。要访问链表中的特定元素，需要从头节点开始按顺序遍历。

缺点：
链表访问节点效率较低。
链表的内存占用较大。
随机访问效率低。

常见链表类型：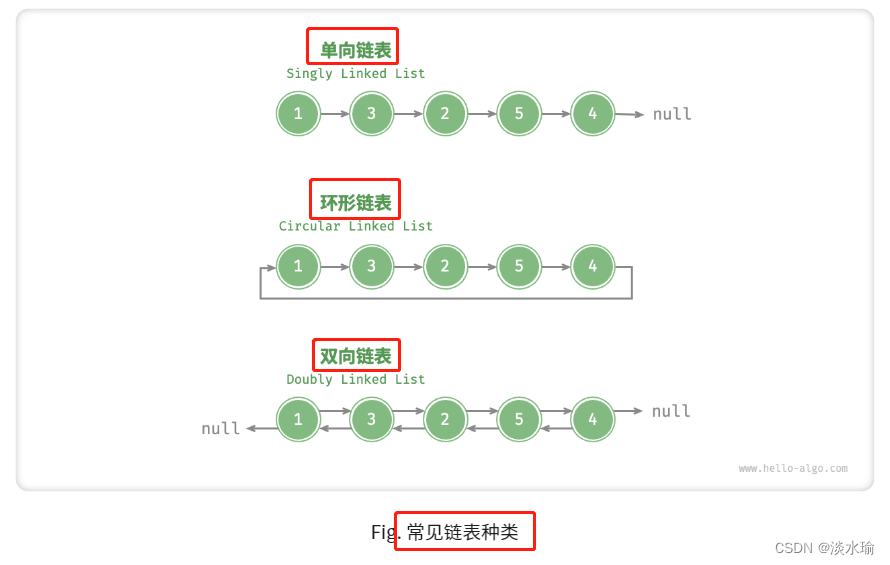

js中基本使用：

// 创建链表节点对象
function ListNode(val) {
  this.val = val; // 存储的值
  this.next = null; // 指向下一个节点的指针
}

// 创建链表
const head = new ListNode(1); // 头节点
const second = new ListNode(2); // 第二个节点
const third = new ListNode(3); // 第三个节点

// 链接节点
head.next = second;
second.next = third;


// 遍历链表
let currentNode = head;
while (currentNode !== null) {
  console.log(currentNode.val); // 打印当前节点的值
  currentNode = currentNode.next; // 移动到下一个节点
}

列表

"列表"通常指的是动态的、灵活大小的数据结构，而"数组"通常指的是固定大小的、连续的内存空间。在JavaScript中，我们使用"数组"来表示有序的数据集合，并且它具有动态的大小和灵活的操作。

栈与队列

栈

栈（Stack）是一种数据结构，它遵循先进后出（Last-In-First-Out，LIFO）的原则。在栈中，最后添加的元素首先被移除，而最先添加的元素最后被移除。栈可以通过两个基本操作进行操作：

1. 入栈（Push）：将元素添加到栈的顶部。
2. 出栈（Pop）：从栈的顶部移除元素。

除了这两个基本操作，栈还具有其他常用的操作，如查看栈顶元素（Peek）和判断栈是否为空（isEmpty）。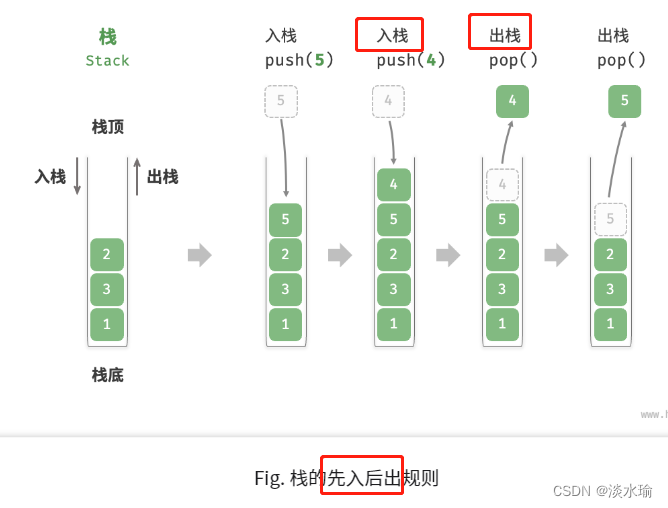

常用操作：

在JavaScript中，可以使用数组或链表来实现栈
class Stack {
    constructor() {
      this.items = [];
    }
  
    push(element) {
      this.items.push(element);
    }
  
    pop() {
      if (this.isEmpty()) {
        return null;
      }
      return this.items.pop();
    }
  
    peek() {
      if (this.isEmpty()) {
        return null;
      }
      return this.items[this.items.length - 1];
    }
  
    isEmpty() {
      return this.items.length === 0;
    }
  
    size() {
      return this.items.length;
    }
  
    clear() {
      this.items = [];
    }
  }

栈的典型应用：

队列

双向队列

二分查找

散列表

哈希表

哈希冲突处理

树

二叉树

二叉树遍历

二叉树数组表示

二叉搜索树

堆

图

图

图基础操作

图的遍历

排序算法

排序算法

冒泡排序

插入排序

快速排序

归并排序

桶排序

计数排序

基数排序

搜索算法

搜索算法

哈希优化策略

回溯算法

回溯算法

全排列问题

N皇后问题

附录

建议，github仓下载源码，zip安装包直接下载。
打开vscode，我用的是javascript的环境，安装node.js。文章来源地址https://uudwc.com/A/AAXkx

1. 下载并安装 node.js 。
2. 在 VSCode 的插件市场中搜索 javascript ，安装 JavaScript (ES6) code snippets 。
3. （可选）在 VSCode 的插件市场中搜索 Prettier ，安装代码格式化工具。