????欢迎来到本博客❤️❤️??
?博主优势:???博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
???本文目录如下:???
目录
?1 概述
?2 运行结果
?3 参考文献
?4 Matlab代码实现
?1 概述
一维粒子滤波(1D Particle Filter)是一种基于粒子的滤波算法,用于估计一个系统中的状态变量。下面是对一维粒子滤波的概述:
1. 系统建模:首先,需要建立系统的状态空间模型。一维粒子滤波通常描述为一个动态系统,其中状态变量在时间步中随机演化。这可以通过一个状态转移函数来建模,通常假设系统的演化是非线性的。
2. 粒子表示:在一维粒子滤波中,使用一组粒子来表示对状态变量的估计。每个粒子都是一个状态假设,对系统的可能状态进行采样,可以使用随机数生成方法来生成粒子。
3. 重采样:随着时间推移和系统演化,粒子的权重会发生变化。在一维粒子滤波中,需要对粒子进行重采样,以根据它们的权重重新分配粒子的数量。重采样的目的是为了保留那些具有较高权重的粒子,去除那些权重较低的粒子。
4. 状态更新:根据测量观测值,需要对粒子进行状态更新。这是通过计算每个粒子的观测概率来实现的。观测概率度量了一个粒子与测量值之间的一致性,可以使用测量模型来计算。
5. 状态估计:根据粒子的权重,可以计算系统状态的估计值。一种常见的方法是使用粒子的加权平均值作为状态的估计,其中权重反映了粒子的可能性。
一维粒子滤波是一种基于贝叶斯滤波原理的非参数滤波方法,可以用于状态估计和跟踪问题。它适用于非线性系统和非高斯噪声的情况,并且能够处理多模态分布。然而,粒子滤波的效率和精度受到粒子数目的影响,过多的粒子会导致计算复杂度增加,而过少的粒子会引入估计误差。
以上是对一维粒子滤波的概述,涉及系统建模、粒子表示、重采样、状态更新和状态估计等关键步骤。具体的应用案例和算法细节可以根据实际问题进行调整和扩展。
?2 运行结果
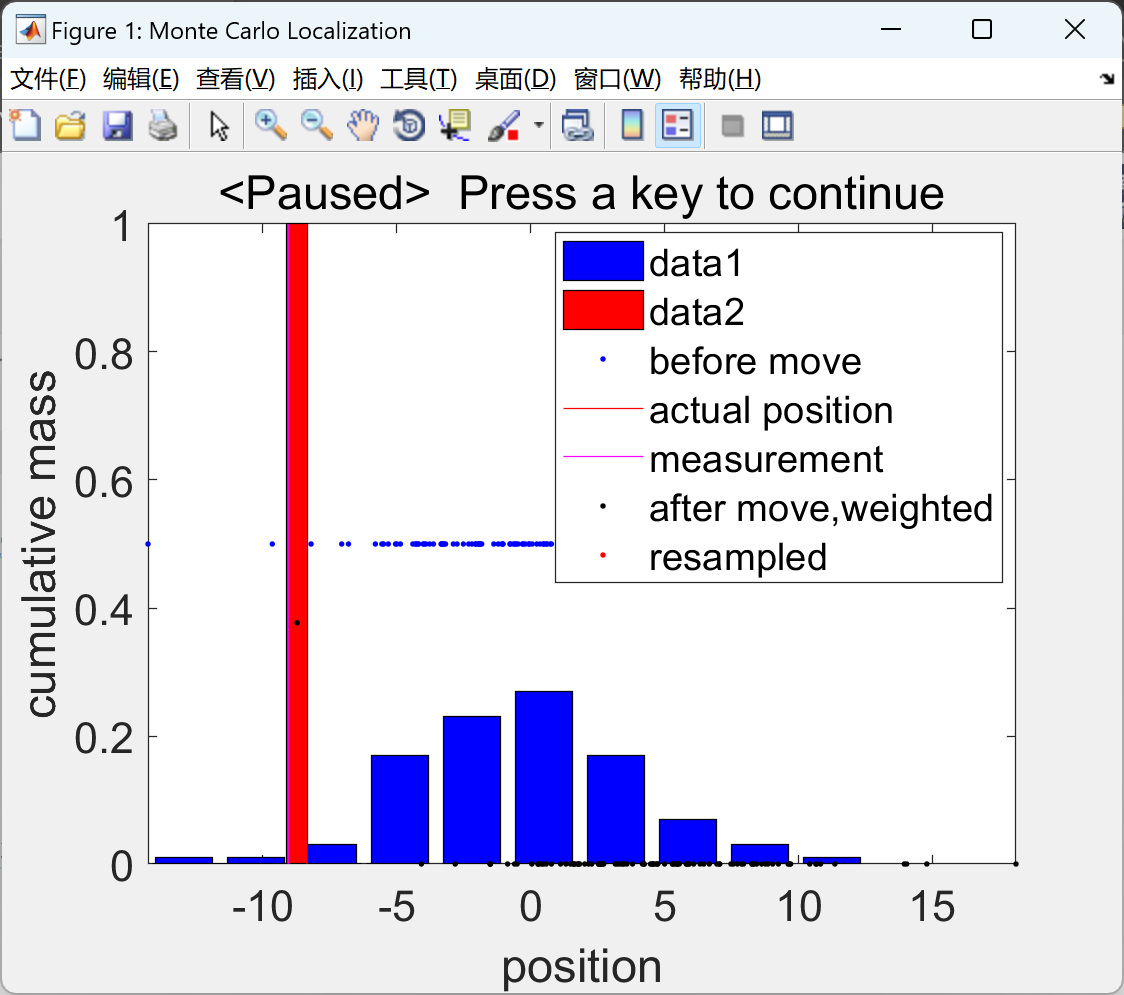
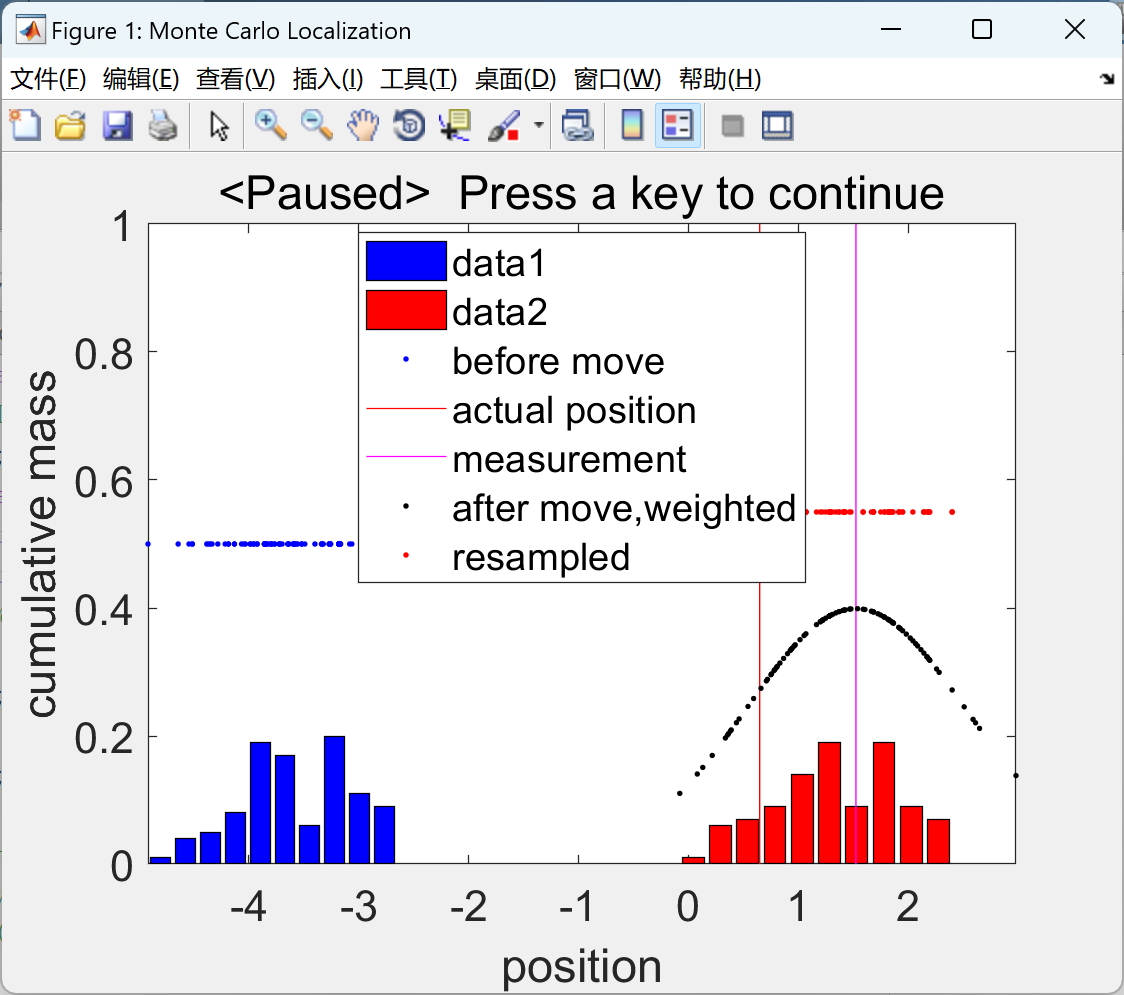
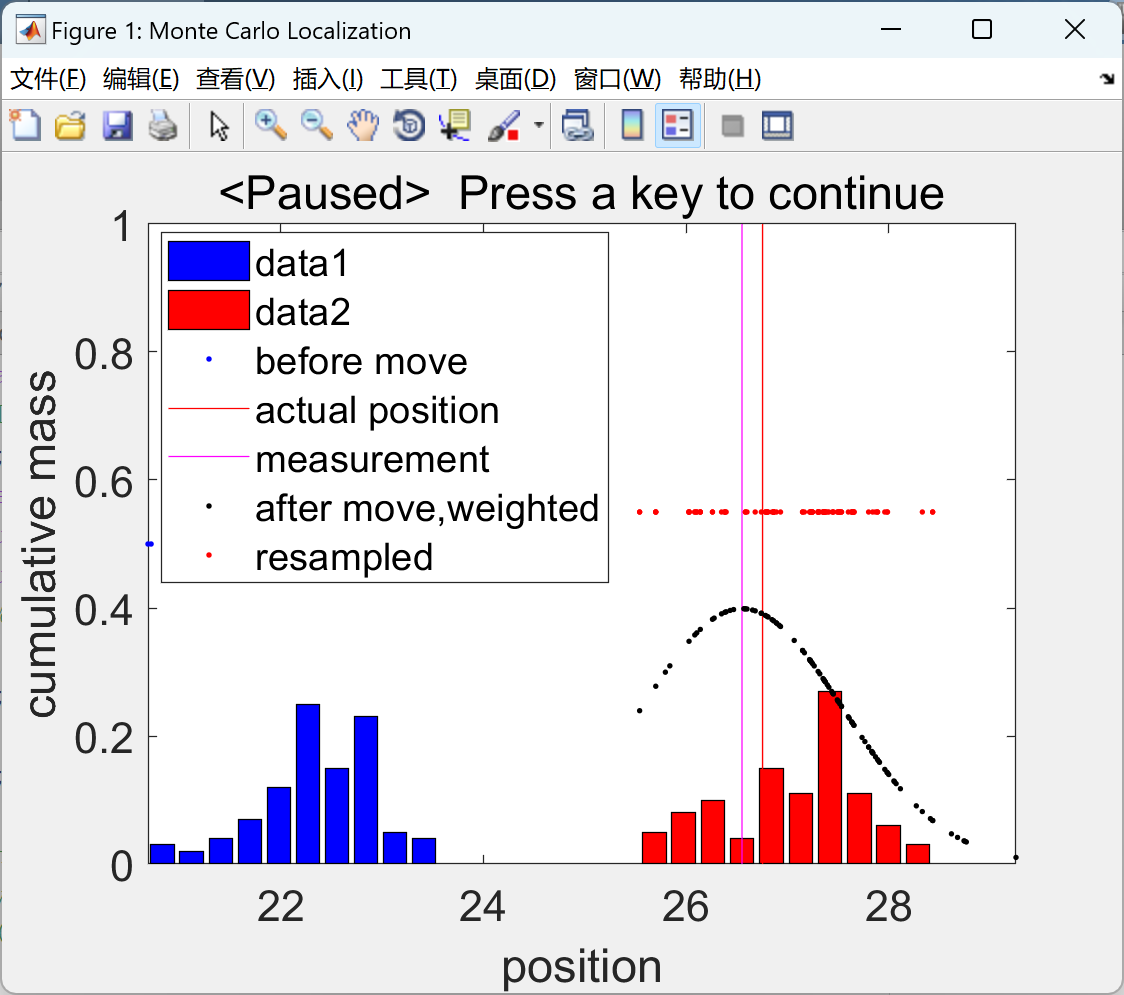
在命令框内按一个键才能逐步完成模拟。以蓝色显示移动前的粒子(带直方图)、用红线移动后的实际位置、用洋红色线显示的测量值、运动模型向前传播并根据测量值加权的粒子(以黑色显示),以红色显示重采样粒子(带直方图)


部分代码:
%%% PLOT SETTINGS %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f1 = figure;
set(f1,'name', 'Monte Carlo Localization')
set(0,'defaultaxesfontsize',16);
set(0,'defaulttextfontsize',16);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
SIGmeas = 1; %standard deviation of measurement noise
SIGproc = 0.5; %standard deviation of process noise
SIGinit = 4; %standard deviation of initial position
M = 100; %number of particles (the more, the better the particle
%Probability Mass Function (PMF) matches the true Probability Distribution
% Function (PDF).
CHI = [SIGinit*randn(M,1), ones(M,1)/M]; %array of particles and associated weights
xACTt = SIGinit*randn(1); %true position of the robot (unknown to particles)
ut = 5; %control input (constant motion in x-direction)
max_moves = 10;
for mv = 1:max_moves
% move ACTUAL robot
xACTt = sample_motion_model(ut, xACTt, SIGproc);
%take measurement
?3 参考文献
部分理论来源于网络,如有侵权请联系删除。
1. 杨琛, 孟翔宇, 李绪连. (2017). 一维离散曲线上的粒子滤波算法. 计算机科学, 44(11), 261-263.
2. 吉宇峰, 赵孜辰, 李燕. (2016). 一维非线性系统的粒子滤波算法研究. 计算机科学与探索, 10(7), 767-775.
3. 孙增茹, 吴琳, 张良康. (2015). 基于一维粒子滤波算法的离散状态系统状态估计. 控制工程, 22(5), 826-829.文章来源:https://uudwc.com/A/ABwGE
4. 赵凯, 张余波, 郑劲松等. (2016). 基于动力系统的一维离散状态粒子滤波算法研究. 电子与信息学报, 38(9), 2359-2366.文章来源地址https://uudwc.com/A/ABwGE