文章目录
- 前言
- 一、密码学
- 1、密码学定义
- 2、密码体制
- 3、通信信道
- 4、算法设计的公开原则
- 5、密码分析
- 5.1、数学类分析方法
- 5.1.1、差分分析
- 5.1.2、线性分析
- 5.1.3、代数分析
- 5.2、旁路攻击方法
- 二、古典密码
- 1、移位密码
- 2、代换密码
- 3、仿射密码
- 4、传统密码
- 4.1、维吉尼亚密码
- 4.2、希尔密码
- 4.3、置换密码
- 5、一次一密
- 6、密码系统
- 三、对称密码
- 1、分组密码
- 1.1、分组密码设计理论
- 1.2、分组密码的结构
- 1.3、分组密码的整体结构
- 1.4、分组密码的工作模式
- 2、DES算法
- 2.1、算法背景
- 2.2、整体结构
- 2.3、DES算法的轮函数
- 2.4、DES算法密钥扩展算法
- 2.5、DES的安全性分析
- 2.6、多重DES
- 2.6.1、二重DES
- 2.6.2、三重DES
- 3、AES算法
- 3.1、AES简介
- 3.2、AES S盒-SB
- 3.3、AES行移位变换-SR
- 3.4、AES列变换-MC
- 3.5、密钥扩展算法
- 3.6、AES-128安全性分析
- 4、Camellia算法
- 4.1、加密过程
- 4.2、安全性分析
- 5、其他分组密码算法
- 6、流密码
- 6.1、同步流密码
- 6.2、异步流密码
- 6.3、RC4
- 四、哈希函数
- 1、SHA
- 2、MD
- 结束!
前言
本篇讲述古典密码、对称密码、哈希函数等内容。
一、密码学
1、密码学定义
-
密码学(Cryptology):研究密码系统或通信安全的一门科学。
- 密码编码学(Cryptography):寻求保证消息保密性或认证性的方法。
- 密码分析学(Cryptanalytics):研究加密消息的破译或消息的伪造。
2、密码体制
定义: 一个密码体制是满足以下条件的五元组 ( ? , ? , ? , E , ? ) (?,?,?,ℰ,?) (P,C,K,E,D):
-
?
?
P表示所有可能的
明文组成的有限集; -
?
?
C表示所有可能的
密文组成的有限集; -
?
?
K表示密钥空间,是由所有可能的
密钥组成的有限集; - 对任意的 K ∈ ? K\in ? K∈K,都存在一个加密法则 e K ∈ E e_K\in ℰ eK∈E和相应的解密法则 d K ∈ ? d_K\in ? dK∈D。并且对每个 e K : ? → ? e_K:?\rightarrow? eK:P→C和 d K : ? → ? d_K:?\rightarrow ? dK:C→P,对任意的明文 x ∈ ? x\in ? x∈P,均有 d K ( e K ( x ) ) = x d_K(e_K(x))=x dK(eK(x))=x。
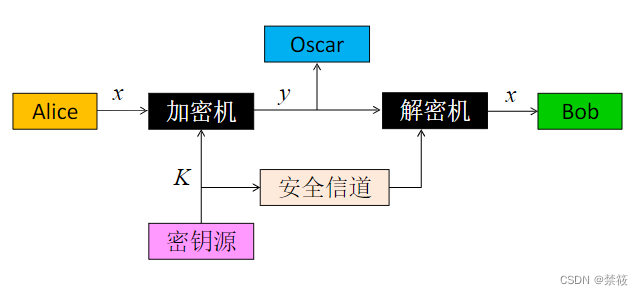
3、通信信道
4、算法设计的公开原则
柯克霍夫原则(Kerckhoffs’ Principle):密码系统安全是基于密钥的而不是算法的保密。
5、密码分析
-
密码分析: 如果能够对密文的分析确定明文或密钥,或者能够根据明文-密文对确定密钥,这个破译过程称为密码分析。
-
数学分析: 密码分析者针对加解密算法的数学基础和某些密码学特性,通过
数学求解的方法来破译密码。 -
物理分析: 针对加密电子设备在运行过程中的时间消耗、功率消耗或电磁辐射之类的
侧信道信息泄露而对加密设备进行攻击的方法被称为侧信道攻击。 -
穷举攻击
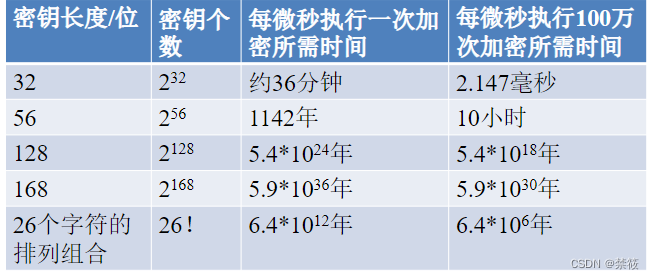
-
密码分析学

5.1、数学类分析方法
- 差分分析及其扩展
- 线性分析及其扩展
- 代数分析
- 相关密钥分析方法
- 其他分析方法
- 积分分析
- 中间相遇分析
- Biclique分析
5.1.1、差分分析
- 差分分析是
选择明文攻击。- 选择明文攻击:密码分析者可得到所需要的任何明文所对应的密文,这些密文与待解的密文是同一个密钥加密得来的。
- 差分的定义(一般情况)
- 对分组长度为n的r轮迭代密码,将两个n比特串 X i X_i Xi和 X i ∗ X_i^* Xi∗的差分定义为: Δ X = X i ⨁ X i ∗ \varDelta X=X_i\bigoplus X_i^* ΔX=Xi⨁Xi∗
- 扩展方法:高阶差分分析,截断差分分析,不可能差分分析,飞来飞去攻击,矩阵攻击。
-
基本思想:通过分析
明文对的差分值对密文对的差分值的影响来恢复某些密钥比特。 - 差分分析一开始是被用来分析DES的安全性,后来被推广到分析所有密码算法的安全性。
- 差分分析是一个非常基本的分析方法,所有的算法在设计之初,设计者就需要考虑它抵抗差分分析的能力。
-
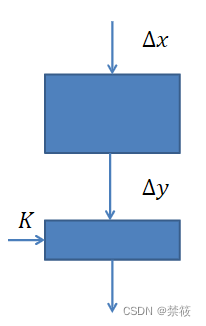
攻击的过程
- 选择大量的4重组 ( x , x ∗ , y , y ∗ ) (x,x^*,y,y^*) (x,x∗,y,y∗),其中 Δ x = x ⨁ x ∗ \varDelta x=x\bigoplus x^* Δx=x⨁x∗, Δ y = y ⨁ y ∗ \varDelta y=y\bigoplus y^* Δy=y⨁y∗的值是固定的。
- 对每个4重组,猜测最后一轮的密钥并进行解密,对每一个候选密钥,计算倒数第二轮的输出差分值;
- 若倒数第二轮的输出差分是 Δ y \varDelta y Δy,此时该猜测密钥的计数器加1;
- 通过计数器的个数多的可能为正确的密钥,因为我们选择一条高概率的差分链。
5.1.2、线性分析
- 扩展方法:多重线性分析,非线性分析,差分-线性分析
- 基本思想:利用密码算法中明文、密文和密钥的不平衡线性逼近来恢复某些密钥比特。
- 线性分析是一种
已知明文攻击- 已知明文攻击:除待解的密文外,密码分析者有一些明文和用同一个密钥加密这些明文所对应的密文。
5.1.3、代数分析

5.2、旁路攻击方法
-
定义: 由于密码算法总是在软件、硬件或物理设备等环境中实现,在运行中总要泄露出各种与密码算法相关的信息,如能量消耗、电磁辐射信息、运行时间等,这些信息被称为
侧信道信息。攻击者利用这些信息攻击密码系统,即为侧信道攻击; -
旁路攻击方式:

二、古典密码
1、移位密码
- 移位密码(Shift Cipher)定义:令 ? = ? = ? = Z 26 ?=?=?=\Z_{26} P=C=K=Z26。对 0 ⩽ K ⩽ 25 0\leqslant K\leqslant 25 0⩽K⩽25,任意 x , y ∈ Z 26 x,y\in\Z_{26} x,y∈Z26,定义加密变换和解密变换分别为 e K ( x ) = ( x + K ) m o d 26 e_K(x)=(x+K)mod26 eK(x)=(x+K)mod26和 d K ( y ) = ( y − K ) m o d 26 d_K(y)=(y-K)mod26 dK(y)=(y−K)mod26。
- 例:
- 密文:L ORYH BRX
- 明文:I LOVE YOU
- 密钥:3
2、代换密码
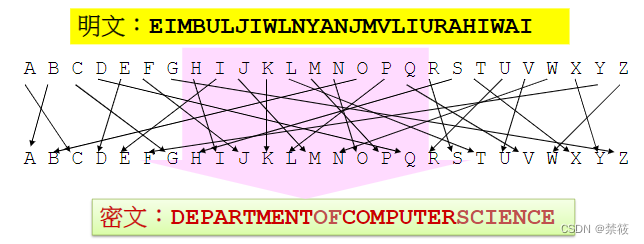
- 代换密码定义:
- 令 ? = ? = Z 26 ?=?=\Z_{26} P=C=Z26, ? ? K由26个数字0,1,···,25的所有可能置换组成。对任意的置换 π ∈ ? \pi\in ? π∈K,定义加密变换和解密变换分别为 e π ( x ) = π ( x ) e_{\pi}(x)=\pi(x) eπ(x)=π(x)和 d π ( y ) = π − 1 ( y ) d_{\pi}(y)={\pi}^{-1}(y) dπ(y)=π−1(y)。
- 例:
3、仿射密码
- 仿射密码定义:
- 令
?
=
?
=
Z
26
?=?=\Z_{26}
P=C=Z26,且
?
=
{
(
a
,
b
)
∈
Z
26
×
Z
26
∣
g
c
d
(
a
,
26
)
=
1
}
?=\{(a,b)\in\Z_{26}\times\Z_{26}|gcd(a,26)=1\}
K={(a,b)∈Z26×Z26∣gcd(a,26)=1}。
gcd()函数为求最大公约数。对任意的 K = ( a , b ) ∈ ? K=(a,b)\in ? K=(a,b)∈K, x , y ∈ Z 26 x,y\in\Z_{26} x,y∈Z26,定义加密变换和解密变换分别为 e K ( x ) = ( a x + b ) m o d 26 e_{K}(x)=(ax+b)mod26 eK(x)=(ax+b)mod26和 d K ( y ) = a − 1 ( y − b ) m o d 26 d_{K}(y)={a}^{-1}(y-b)mod26 dK(y)=a−1(y−b)mod26。
- 令
?
=
?
=
Z
26
?=?=\Z_{26}
P=C=Z26,且
?
=
{
(
a
,
b
)
∈
Z
26
×
Z
26
∣
g
c
d
(
a
,
26
)
=
1
}
?=\{(a,b)\in\Z_{26}\times\Z_{26}|gcd(a,26)=1\}
K={(a,b)∈Z26×Z26∣gcd(a,26)=1}。
- 例:密钥
K
=
(
7
,
3
)
K=(7,3)
K=(7,3),加密变换
e
K
(
x
)
=
7
x
+
3
e_{K}(x)=7x+3
eK(x)=7x+3;由于
7
−
1
m
o
d
26
=
15
7^{-1}mod26=15
7−1mod26=15,所以解密变换
d
K
(
y
)
=
15
(
y
−
3
)
m
o
d
26
=
15
y
−
19
d_{K}(y)=15(y-3)mod26=15y-19
dK(y)=15(y−3)mod26=15y−19。
PS:这里的-1是取逆元而不是倒数。
4、传统密码
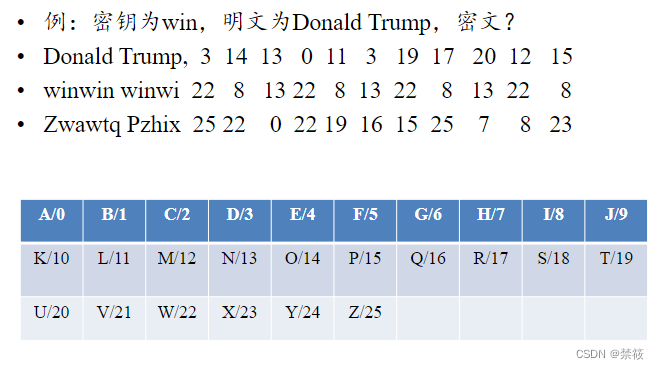
4.1、维吉尼亚密码
设m是一个正整数。定义 ? = ? = ? = ( Z 26 ) m ?=?=?=(\Z_{26})^m P=C=K=(Z26)m。对任意的密钥 K = ( k 1 , k 2 , ⋯ , k m ) K=(k_1,k_2,\cdots,k_m) K=(k1,k2,⋯,km),定义加密和解密算法分别为: e K ( x 1 , x 2 , ⋯ , x m ) = ( x 1 + k 1 , x 2 + k 2 , ⋯ , x m + k m ) e_K(x_1,x_2,\cdots,x_m)=(x_1+k_1,x_2+k_2,\cdots,x_m+k_m) eK(x1,x2,⋯,xm)=(x1+k1,x2+k2,⋯,xm+km)和 d K ( y 1 , y 2 , ⋯ , y m ) = ( y 1 − k 1 , y 2 − k 2 , ⋯ , y m − k m ) d_K(y_1,y_2,\cdots,y_m)=(y_1-k_1,y_2-k_2,\cdots,y_m-k_m) dK(y1,y2,⋯,ym)=(y1−k1,y2−k2,⋯,ym−km),以上所有的运算均在 Z 26 \Z_{26} Z26上进行。
4.2、希尔密码
设 m ⩾ 2 m\geqslant 2 m⩾2为正整数, ? = ? = ( Z 26 ) m ?=?=(\Z_{26})^m P=C=(Z26)m,且 ? = { 定义在 ( Z 26 ) 上的 m × m 可逆矩阵 } ?=\{定义在(\Z_{26})上的m\times m可逆矩阵\} K={定义在(Z26)上的m×m可逆矩阵}。对任意的密钥K,定义加密变换和解密变换分别为 e K ( x ) = x K e_K(x)=xK eK(x)=xK和 d K ( y ) = y K − 1 d_K(y)=yK^{-1} dK(y)=yK−1以上所有的运算均在 Z 26 \Z_{26} Z26上进行。
4.3、置换密码
设m是一个正整数。定义 ? = ? = ( Z 26 ) m ?=?=(\Z_{26})^m P=C=(Z26)m。 ? ? K由所有定义在集合 { 1 , 2 , ⋯ , m } \{1,2,\cdots,m\} {1,2,⋯,m}上的置换组成。对任意的密钥(置换) π \pi π,定义加密算法和解密算法分别为: e K ( x 1 , x 2 , ⋯ , x m ) = ( x π ( 1 ) , ⋯ , x π ( m ) ) e_K(x_1,x_2,\cdots,x_m)=(x_{\pi(1)},\cdots,x_{\pi(m)}) eK(x1,x2,⋯,xm)=(xπ(1),⋯,xπ(m))和 d K ( y 1 , ⋯ , y m ) = ( y π − 1 ( 1 ) , ⋯ , y π − 1 ( m ) ) d_K(y_1,\cdots,y_m)=(y_{\pi^{-1}(1)},\cdots,y_{\pi^{-1}(m)}) dK(y1,⋯,ym)=(yπ−1(1),⋯,yπ−1(m)),上式中 π − 1 \pi^{-1} π−1为置换 π \pi π的逆置换。
5、一次一密
假设 n ⩾ 1 n\geqslant 1 n⩾1是正整数, ? = ? = ? = ( Z 2 ) n ?=?=?=(\Z_{2})^n P=C=K=(Z2)n。对于 K ∈ ( Z 2 ) n K\in(\Z_{2})^n K∈(Z2)n,定义 e K ( x ) e_K(x) eK(x)为K和x的模2的向量和(或者说是两个相关比特串的异或)。因此,如果 x = ( x 1 , ⋯ , x n ) x=(x_1,\cdots,x_n) x=(x1,⋯,xn)并且 K = ( K 1 , ⋯ , K n ) K=(K_1,\cdots,K_n) K=(K1,⋯,Kn),则 e K ( x ) = ( x 1 + K 1 , ⋯ , x n + K n ) m o d 2 e_K(x)=(x_1+K_1,\cdots,x_n+K_n)\mod 2 eK(x)=(x1+K1,⋯,xn+Kn)mod2,解密和加密是一样的。如果 y = ( y 1 , ⋯ , y n ) y=(y_1,\cdots,y_n) y=(y1,⋯,yn),则 d K ( y ) = ( y 1 + K 1 , ⋯ , y n + K n ) m o d 2 d_K(y)=(y_1+K_1,\cdots,y_n+K_n)\mod 2 dK(y)=(y1+K1,⋯,yn+Kn)mod2。
PS:1、密钥的长度要和明文消息的长度一致;
2、每次加密所使用的密钥都需要随机选取。
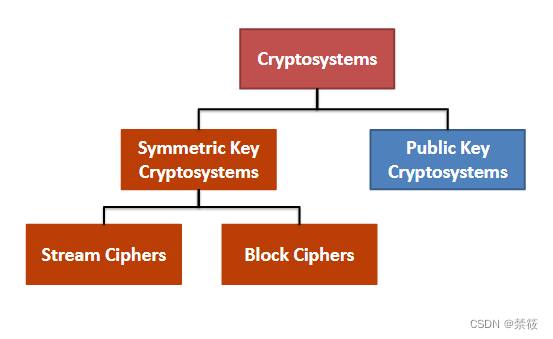
6、密码系统
三、对称密码
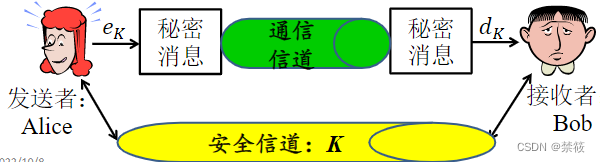
- 对称密码定义: 加解密使用相同密钥的密码体制。
- 对称密码:
- 分组密码: 是一种加解密方案,它将输入的明文分组当做一个整体处理,输出一个等长的密文分组;
- DES,AES,Blowfish,Twofish,Skipjack,和RC2
- 轻量级分组密码:LBlock,Present,SIMON,SPECK,LED等。
- 流密码: 从明文输入流逐位或逐字节产生密文输出。RC4,ZUC,A5等。
1、分组密码
- 分组密码定义: 将明文分组消息编码表示后的数字(通常是0或1)序列 x 1 , x 2 , ⋯ x_1,x_2,\cdots x1,x2,⋯划分成长为m的组 x = ( x 1 , x 2 , ⋯ , x m ) x=(x_1,x_2,\cdots,x_m) x=(x1,x2,⋯,xm),各组(长为m的向量)分别在密钥 k = ( k 1 , k 2 , ⋯ , k t ) k=(k_1,k_2,\cdots,k_t) k=(k1,k2,⋯,kt)的控制下变换成等长的输出数学序列 y = ( y 1 , y 2 , ⋯ , y n ) y=(y_1,y_2,\cdots,y_n) y=(y1,y2,⋯,yn)(长度为n的向量)。
-
数学模型:
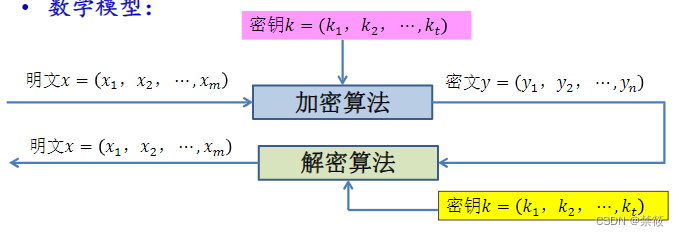
-
分组密码形式化定义:
- 分组密码是一种满足下列条件的映射 E : S K × F 2 m E:S_K\times F_2^m E:SK×F2m:对每个 k ∈ S K k\in S_K k∈SK, E ( k ) E(k) E(k)是从 F 2 m F_2^m F2m到 F 2 m F_2^m F2m的一个置换。
-
分类:
- 若
n
>
m
n>m
n>m,称为
有数据扩展的分组密码; - 若
n
<
m
n<m
n<m,称为
有数据压缩的分组密码; - 若
n
=
m
n=m
n=m,称为
无数据扩展或压缩的分组密码(通常均为此类)
- 若
n
>
m
n>m
n>m,称为
- 优点:
- 分组密码容易被标准化
- 分组密码同意实现同步
- 缺点:
- 分组密码不能隐蔽数据模式
- 分组加密不能抵抗重放、嵌入和删除等攻击
1.1、分组密码设计理论
- 针对安全性的设计原理
- 混淆原则: 人们所设计的密码应使得密钥和明文以及密文之间的依赖关系相当复杂,以至于这种依赖性对密码分析者来说无法利用;
- 扩散原则: 人们所设计的密码应使得密钥的每一位影响密文的许多位,以防止对密钥进行逐段破译;而且明文的每一位也应该影响密文的许多位,以便隐蔽明文的统计特性。
- 针对实现的设计原理
- 软件实现的设计方案: 使用子块和简单运算
- 硬件实现的设计方案: 加密和解密的相似性,以便同样的器件可以用来加解密。
1.2、分组密码的结构
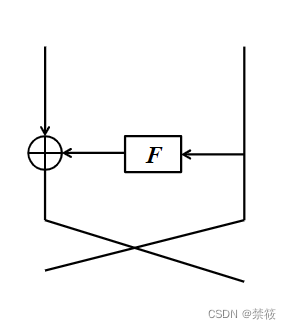
Feistel结构
- 一轮加密过程
- L 1 = R 0 L_1=R_0 L1=R0
- R 1 = L 0 ⊕ F ( R 0 , K 0 ) R_1=L_0\oplus F(R_0,K_0) R1=L0⊕F(R0,K0)
- 加解密相似
1.3、分组密码的整体结构
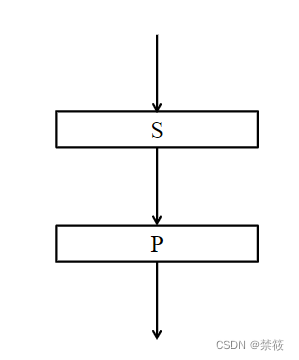
SP结构
- S:Substitution(替换),混淆层
- P:Permutation(置换),扩散层
- 和Feistel结构相比,SP结构可以得到更快的扩散,更适宜硬件实现
1.4、分组密码的工作模式
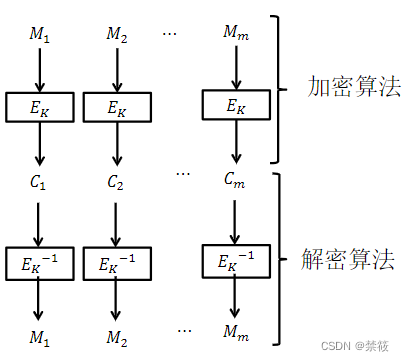
- ECB(Electronic Codebook,电码本模式)
- 优点:
- 可并行运算
- 速度快
- 易于标准化
- 缺点:
- 分组密码不能隐蔽数据格式
- 不能抵抗重放、嵌入、删除
- 加密长度只能是分组的倍数
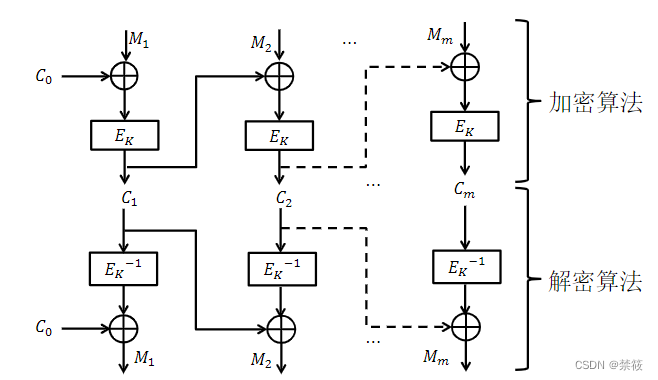
- CBC(Cipher Block Chaining,密码链接模式)
- 优点:输出具有一定的随机性,在一定程度上防止数据篡改。
- 缺点:
- 会出现错误传播
- 加密的消息只能说分组长度的倍数
- CTR(Counter Moder,计数器模式)
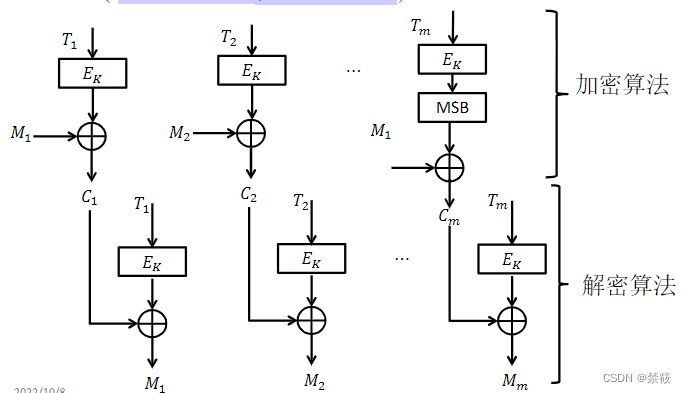
2、DES算法
2.1、算法背景

2.2、整体结构
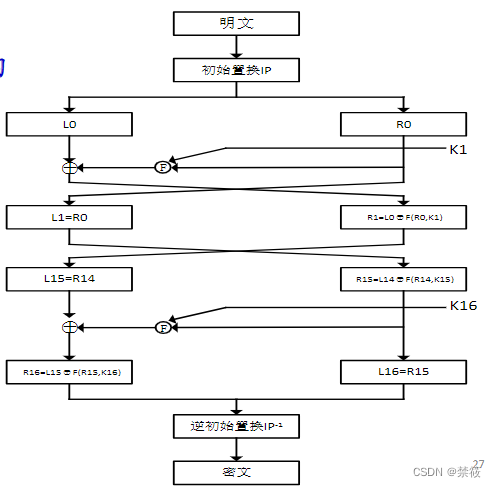
- 明文长度、密钥长度、密文长度:64bit,56bit,64bit;
- 轮数:16轮
- 加密算法:
- x 0 = I P ( x ) = L 0 R 0 x_0=IP(x)=L_0R_0 x0=IP(x)=L0R0,其中x是明文, L 0 L_0 L0是 x 0 x_0 x0左32比特, R 0 R_0 R0是 x 0 x_0 x0右32比特;
- L i = R i − 1 : R i = L i − 1 ⊕ f ( R i − 1 , K i ) L_i=R_{i-1}:R_i=L_{i-1}\oplus f(R_{i-1},K_i) Li=Ri−1:Ri=Li−1⊕f(Ri−1,Ki),其中f是轮函数, K i K_i Ki是长度为48比特的第i轮密钥;
- 密文
y
=
I
P
−
1
(
R
16
L
16
)
y=IP^{-1}(R_{16}L_{16})
y=IP−1(R16L16);
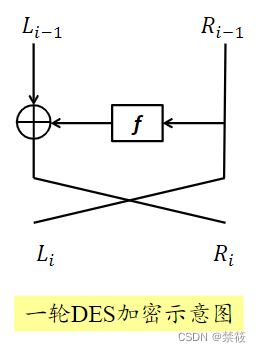
2.3、DES算法的轮函数
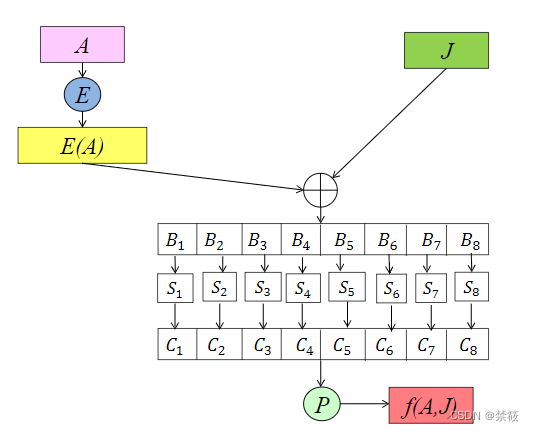
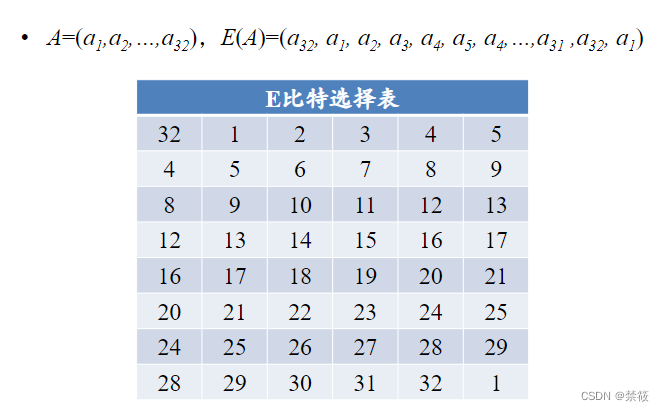

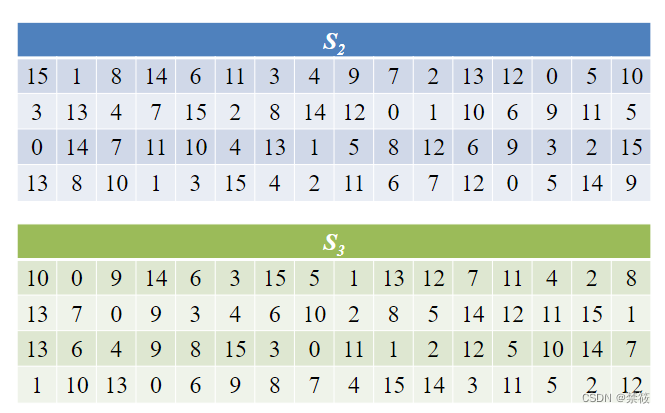
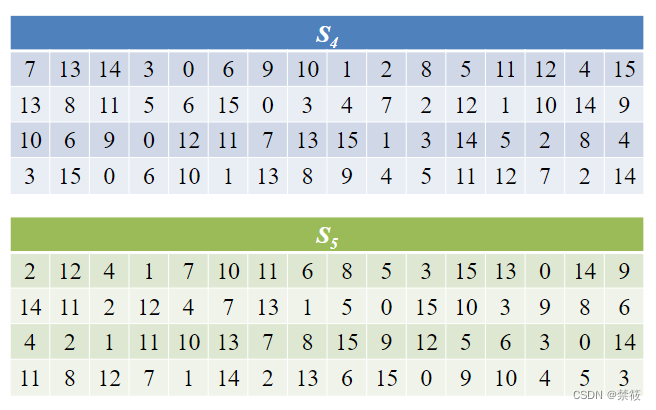
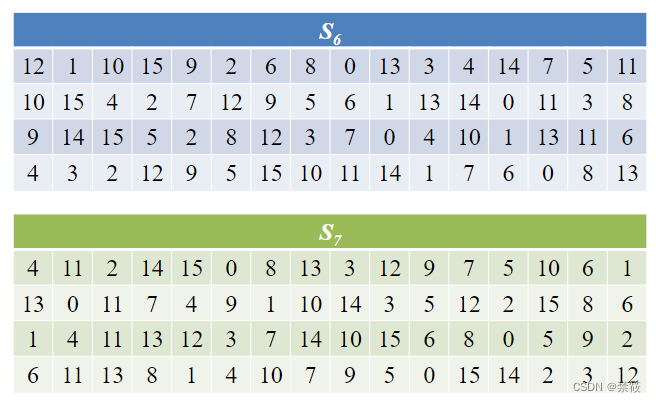
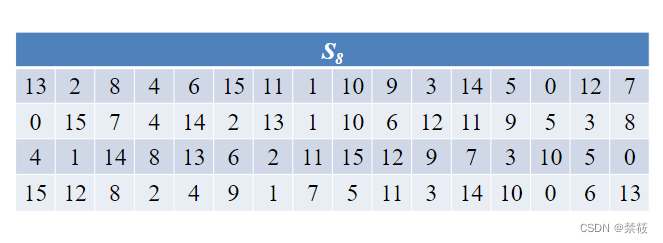
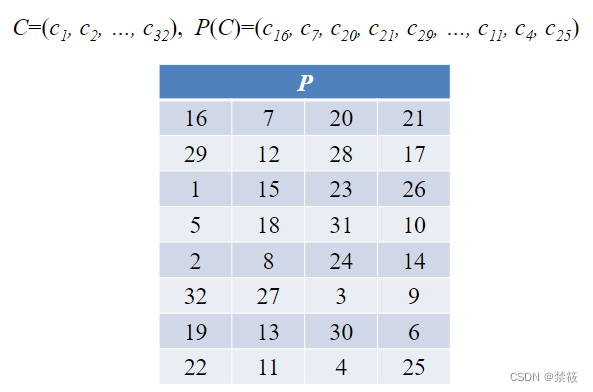
2.4、DES算法密钥扩展算法

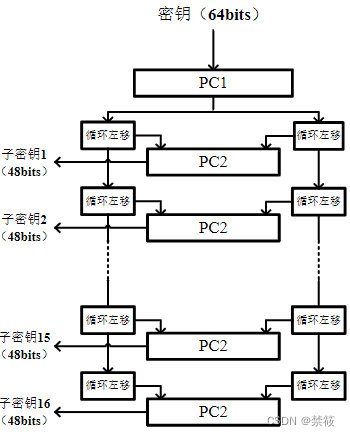
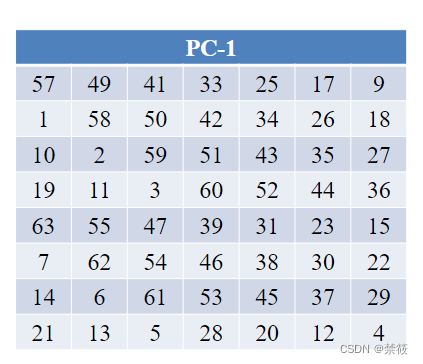
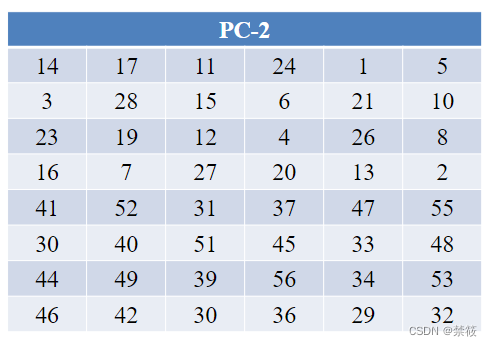
2.5、DES的安全性分析
-
穷尽密钥搜索攻击:
- DES的密钥个数: 2 56 ≈ 1 0 17 2^{56}\approx 10^{17} 256≈1017;
- 1997年1月28日,美国RSA数据安全公司悬赏10000美元破译密钥长度为56比特的DES;
- 从1997年3月13日起,美国科罗拉多州的程序员Verser用了96天成功破译了DES算法;
- 1998年7月,电子边境基金会(EFF)使用了25万美元的计算机在56小时内破解了56比特DES;
- 1999年1月,电子边境基金会(EFF)宣布花了22.5小时破解了DES;
- DES显示了很强的雪崩效应(即明文或密钥的微小改变将对密文产生很大的影响)。
-
DES的弱点:
- 弱密钥:DES中存在着少量弱密钥,即一个主密钥可以产生的所有子密钥都是一样的。
- 密文与明文、密文与密钥的相关性:每个密文位都是所有明文位和所有密钥位的复合函数,达到这一要求所需的迭代次数最少为5,迭代8次以后输出的输入就可认为是不相关的了。
2.6、多重DES
2.6.1、二重DES
-
二重DES: 给定明文P和两个加密密钥
k
1
k_1
k1和
k
2
k_2
k2,采用DES对P进行加密E,有
C
=
E
k
2
(
E
k
1
(
P
)
)
C=E_{k_2}(E_{k_1}(P))
C=Ek2(Ek1(P))。加密过程如下:
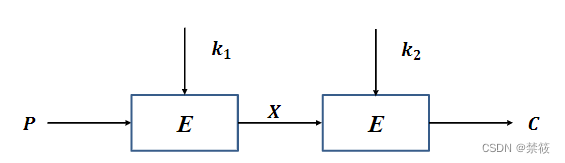
- 利用中间相遇攻击,只需要 2 57 2^{57} 257次迭代就可以恢复出密钥。
2.6.2、三重DES
- 1、使用两个密钥的三重DES
C
=
E
k
1
(
D
k
2
(
E
k
1
(
P
)
)
)
C=E_{k_1}(D_{k_2}(E_{k_1}(P)))
C=Ek1(Dk2(Ek1(P)))密钥长度112bit。
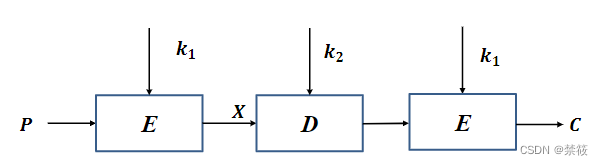
- 2、使用三个密钥的三重DES C = E k 3 ( D k 2 ( E k 1 ( P ) ) ) C=E_{k_3}(D_{k_2}(E_{k_1}(P))) C=Ek3(Dk2(Ek1(P)))密钥长度168bit。
3、AES算法
3.1、AES简介
- 明文长度和密文长度: 128bit
- 密钥长度: 128bit/192bit/256bit
- 轮数 N r N_r Nr: 10轮/12轮/14轮
-
加密过程:
- 128bit明文P看成是16个 G F ( 2 8 ) GF(2^8) GF(28)上的元素;
- X 0 = P ⊕ K 0 X_0=P\oplus K_0 X0=P⊕K0;
-
F
o
r
(
i
=
1
)
t
o
(
N
r
−
1
)
For(i=1)to(N_r-1)
For(i=1)to(Nr−1)
- X i = A K ∘ M C ∘ S R ∘ S B ( X i − 1 ) X_i=AK∘MC∘SR∘SB(X_{i-1}) Xi=AK∘MC∘SR∘SB(Xi−1)
- 密文
C
=
A
K
∘
S
R
∘
S
B
(
X
N
r
−
1
)
C=AK∘SR∘SB(X_{N_r-1})
C=AK∘SR∘SB(XNr−1)
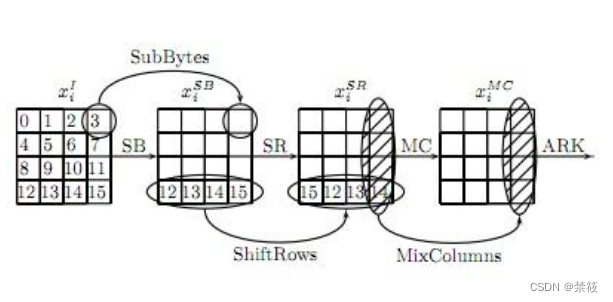
3.2、AES S盒-SB
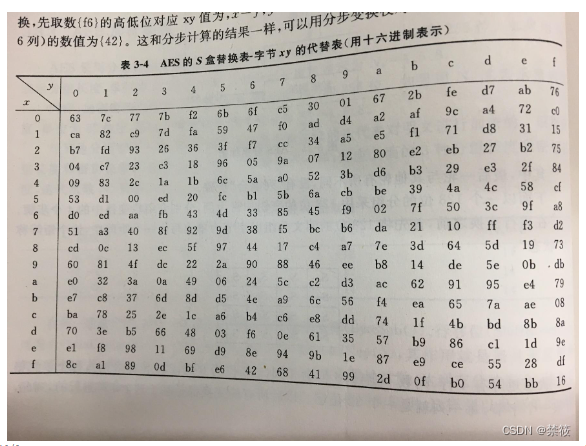
解释一下,
4
×
4
4\times 4
4×4的矩阵,每一个元素8bit,左4bit为x(十进制),右4bit为y(十进制),然后查表就行了。
3.3、AES行移位变换-SR
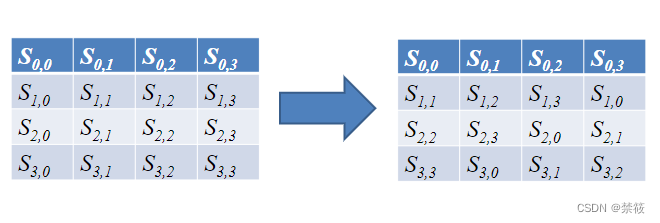
第一行左移0个元素,第二行左移1个元素,以此类推。
3.4、AES列变换-MC
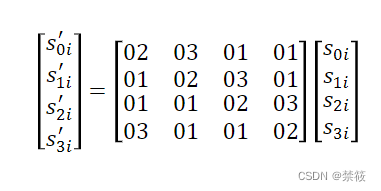
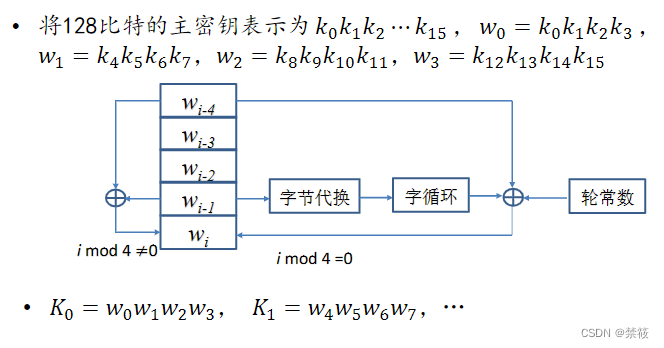
3.5、密钥扩展算法
3.6、AES-128安全性分析
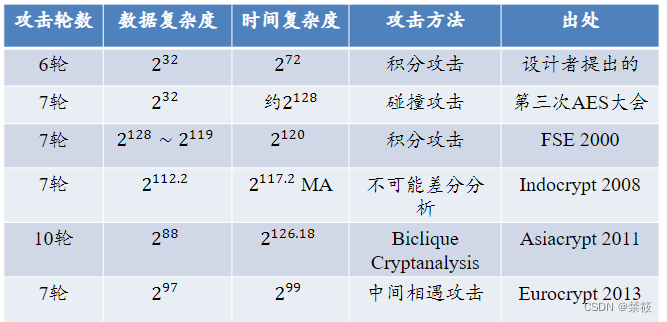
4、Camellia算法
4.1、加密过程
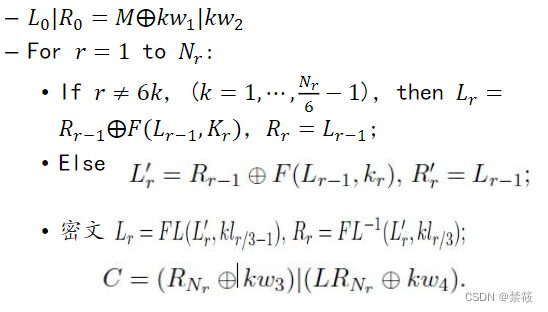
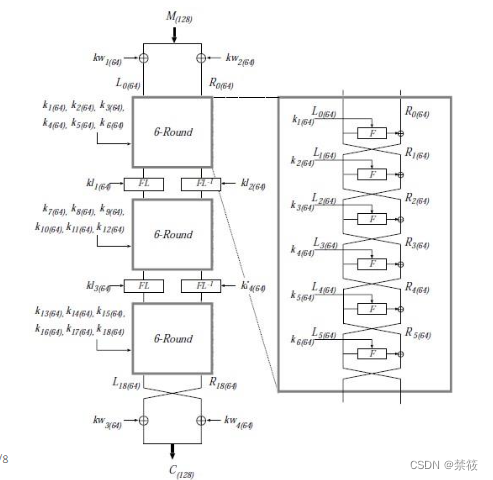
4.2、安全性分析
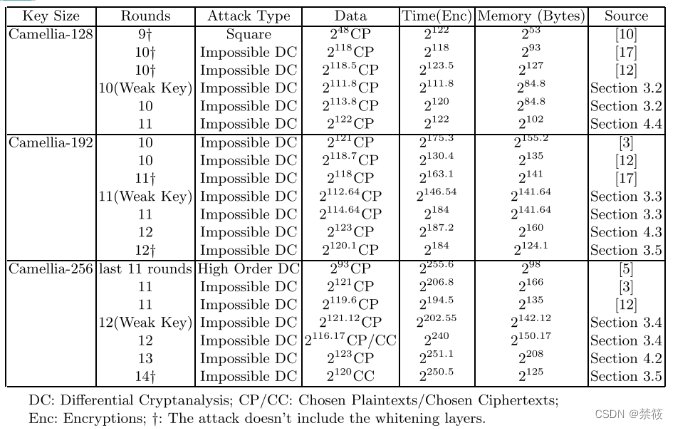
最新结果: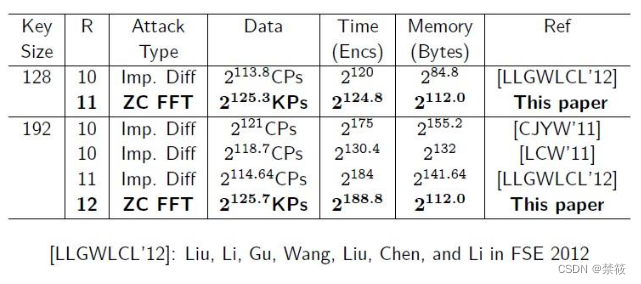
5、其他分组密码算法
- SMS4
- ARIA
- CLEAFIA
- IDEA
- Serpent
6、流密码
- 一个流密码将消息分成连续的符号 x = x 1 x 2 ⋯ x=x_1x_2\cdots x=x1x2⋯,用密钥流 k = k 1 k 2 ⋯ k=k_1k_2\cdots k=k1k2⋯的第i个元素 k i k_i ki对 x i x_i xi加密,即 E k ( x ) = E k 1 ( x 1 ) E k 2 ( x 2 ) ⋯ E_k(x)=E_{k_1}(x_1)E_{k_2}(x_2)\cdots Ek(x)=Ek1(x1)Ek2(x2)⋯;
- 如果密钥流经过d个符号后重复,则称该密钥流是
周期性的,否则就是非周期的。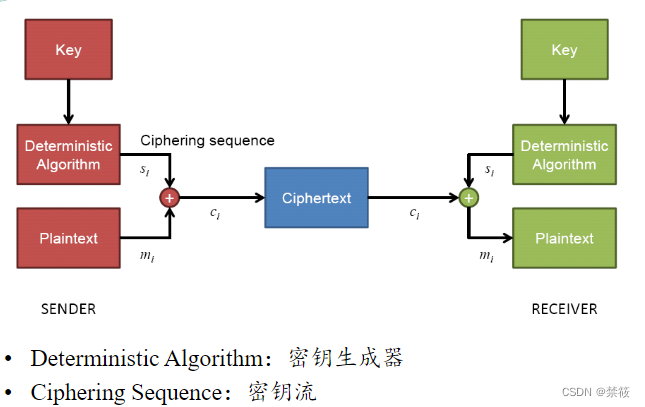
6.1、同步流密码

6.2、异步流密码
定义: 密钥流的产生不但与密钥K有关,而且还与明文元素或密文元素有关。
6.3、RC4

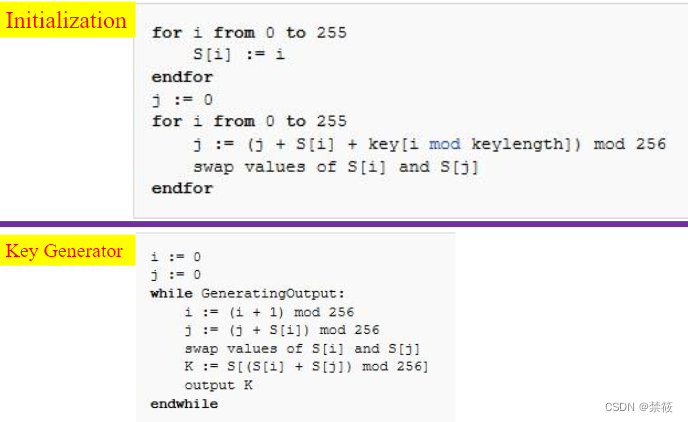
四、哈希函数
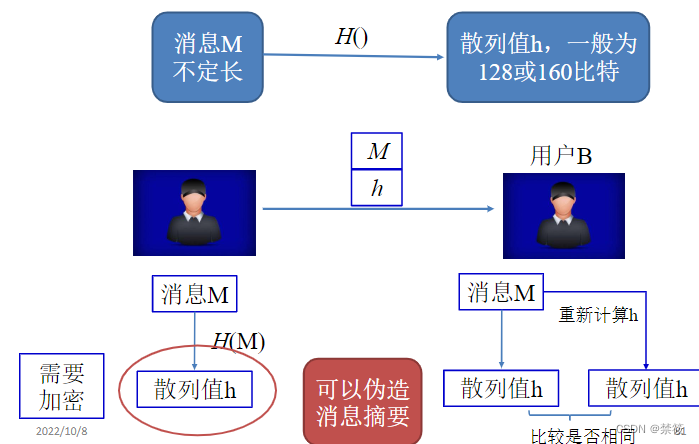
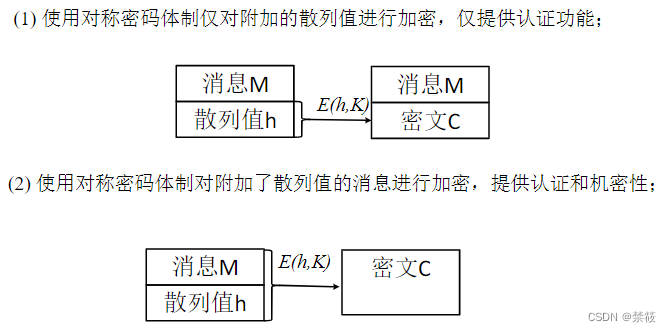
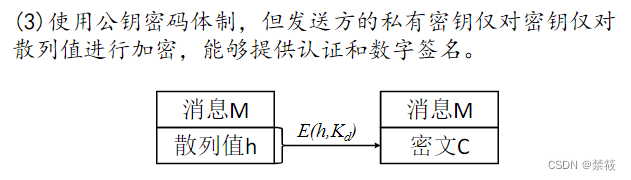
- 哈希函数性质:
- 哈希函数能够适合于各种消息和文件,用途广泛;
- 给定M,计算 H ( M ) H(M) H(M)相对容易;
- 给定 H ( M ) H(M) H(M),计算出M是相对容易的;
- 给定M1,寻找M2,使 H ( M 1 ) = H ( M 2 ) H(M1)=H(M2) H(M1)=H(M2)在计算上不可行;
- 寻找任何的
(
M
1
,
M
2
)
(M1,M2)
(M1,M2),使
H
(
M
1
)
=
H
(
M
2
)
H(M1)=H(M2)
H(M1)=H(M2)在计算上不可行。

1、SHA
 文章来源:https://uudwc.com/A/DzG0B
文章来源:https://uudwc.com/A/DzG0B
2、MD
 文章来源地址https://uudwc.com/A/DzG0B
文章来源地址https://uudwc.com/A/DzG0B
