回归分析是研究一个因变量与一个或多个自变量之间的线性或非线性关系的一种统计分析方法。
下面我们主要从下面四个方面来解说:
- 实际应用
- 理论思想
-
建立模型
- 分析结果
一、实际应用
回归分析方法理论成熟,它可以确定变量之间的定量关系并进行相应的预测,反映统计变量之间的数量变化规律,为研究者准确把握自变量对因变量的影响程度和方向提供有效的方法,在经济、金融和社会科学方面具有广泛的应用。
回归分析研究分析某一变量受其他变量影响的分析方法,它以被影响变量为因变量,以影响变量为自变量,研究因变量与自变量之间的因果关系,包括简单线性回归、多重线性回归、曲线回归、非线性回归、加权最小二乘回归、二阶段最小二乘回归、Logistic回归、最优标度回归等。
1、简单线性回归/多重线性回归
线性回归分析是常用的回归分析,许多非线性的模型形式亦可以转化为线性回归模型进行分析。
2、曲线回归
曲线估计可以拟合许多常用的曲线关系,当变量之间存在可以使用这些曲线描述的关系时,我们便可以使用曲线回归分析进行拟合。3、非线性回归分析
非线性回归分析适用于了解参数的初始值或取值范围,而模型又无法转化为线性模型估计的情况。4、Logistic回归分析
Logistic回归分析常用于因变量为二分变量时的回归拟合。5、有序回归分析
因变量是有序的分类变量,应该使用有序回归的分析方法。6、概率回归分析
概率回归分析适用于对响应比例与刺激作用之间关系的分析,概率回归分析属于SPSS中的专业统计分析过程。7、加权回归分析
模型存在异方差性,可用加权最小二乘法(WLS)进行估计。加权最小二乘法是对原模型加权,使之变成一个新的不存在异方差性的模型,然后采用加权回归方法估算其参数。
二、理论思想
回归分析通过规定因变量和自变量来确定变量之间的因果关系,建立回归模型,并根据实测数据来估计模型的各个参数,然后评价回归模型是否能够很好地拟合实测数据;并可以根据自变量作进一步预测。
回归分析是统计学中的基本分析方法,一般用来解决以下问题:
第一,确定因变量与若干个因素变量之间联系的定量表达式,通常称为回归方程或数学模型,并确定它们联系的密切程度;
第二,通过控制可控变量的数值,借助于求出的数学模型来预测或控制因变量的取值和精度;
第三,进行因素分析,从影响变量变化的因素变量中寻找出哪些因素对因变量的影响最为显著,哪些因素的影响不那么显著,以区别重要因素和次要因素。
回归分析主要研究变量之间的线性关系,称为线性回归分析,线性回归分析是基于最小二乘法原理产生的古典统计假设下的统计分析方法,用来研究一个或多个自变量与一个因变量之间是否存在某种线性关系。
三、建立模型
相关分析的数据条件:
- 线性关系。可以绘制散点图,判断是否存在线性关系。
- 独立性:每个个体观察值之间相互独立,在模型中看残差是否独立。
- 正态性:通过专业知识或残差的散点图来判断这项条件是否满足。
- 方差齐性:在一定范围内,不同的自变量值所对应的随机因变量的方差相等
模型建立的步骤:
回归分析需要结合专业、数据、模型诊断和研究目的,方可建立较优的模型,而且模型也有应用的条件,各行各业的人构建自己模型的必要。
构建模型的步骤如下:
(1)专业考虑;
(2)散点图验证;
(3)建模;
(4)模型验证;
(5)优化模型。
简单线性回归案例:
题目:菲利普斯曲线表明,失业率和通货膨胀率之间存在替代关系。表6.10给出了我国1998~2007年的通货膨胀率和城镇登记失业率。试用简单线性回归分析方法研究这种替代关系在我国是否存在。
一、数据输入
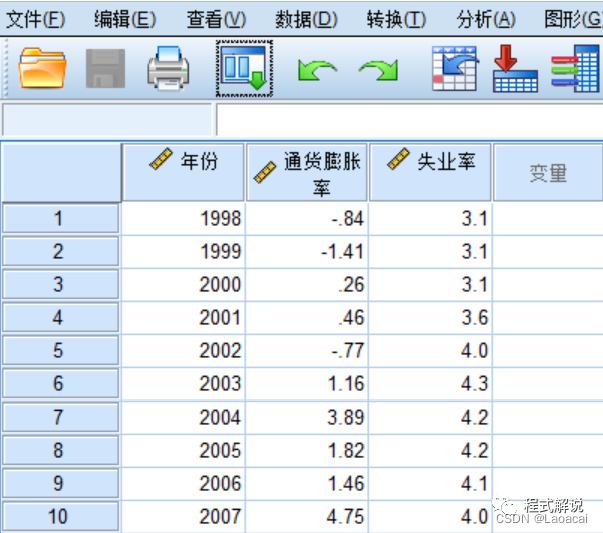
二、操作步骤
1、进入SPSS,打开相关数据文件,选择“分析”|“回归”|“线性”命令2、选择进行简单线性回归分析的变量。在“线性回归”对话框的左侧列表框中,选中“失业率”进入“因变量”列表框,选中“通货膨胀率”进入“自变量”列表框。
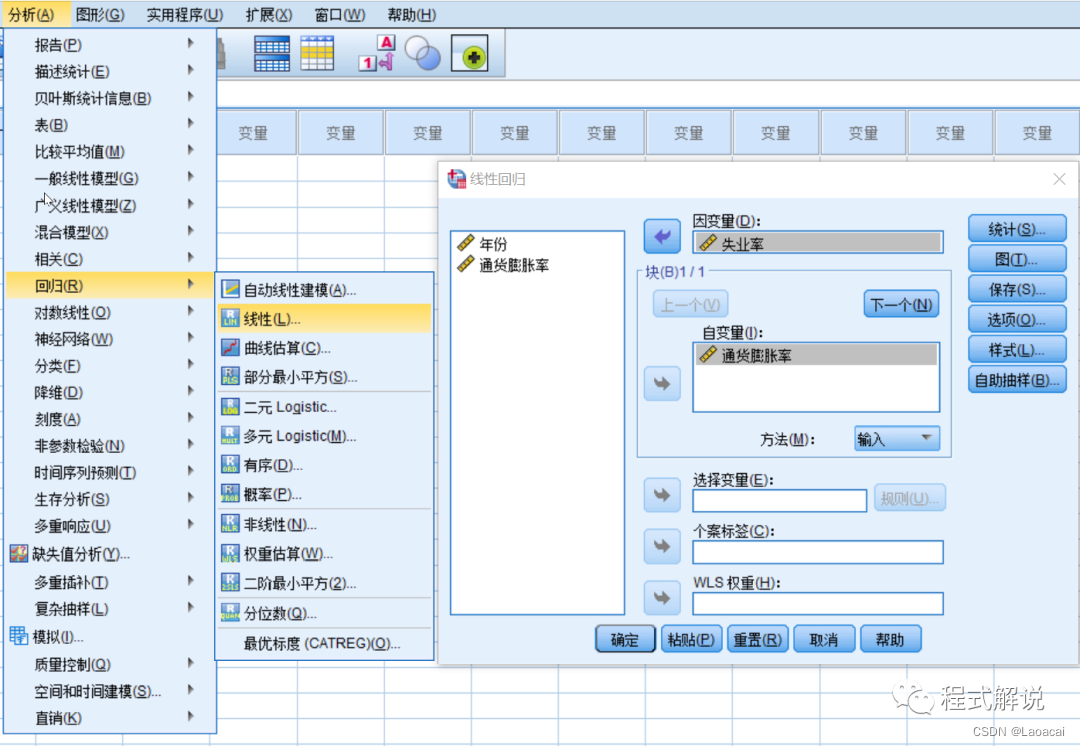
3、其余设置采用系统默认值即可。单击“确定”按钮,等待输出结果。
四、结果分析
1、模型拟合情况模型的拟合情况反映了模型对数据的解释能力。调整后的R平方越大,模型的解释能力越强。
2、方差分析方差分析反映了模型整体的显著性,一般将模型的检验显著性(Sig)与0.05进行比较,如果小于0.05,即为显著。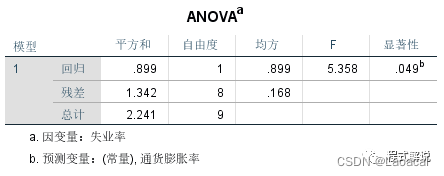
3、回归方程的系数以及系数的检验结果回归方程的系数是各个变量在回归方程中的系数值,显著性表示回归系数的显著性,越小越显著,一般将其与0.05进行比较,如果小于0.05,即为显著。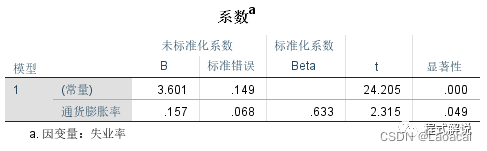
分析结论:对数据进行简单线性回归分析
观察回归方程的系数以及系数的检验结果:我们可以写出最终模型的如下表达式,这意味着通货膨胀率每增加1,失业率就增加0.157点:R(失业率)=3.601+0.157*I(通货膨胀率)
观察模型拟合情况:模型的拟合优度也就是对数据的解释能力一般,调整后的R平方为0.326。
观察方差分析:模型是显著的,显著性水平为0.049,小于0.05。
观察回归方程的系数以及系数的检验结果:模型中常数项是3.601,t值是24.205,显著性是0.000;通货膨胀率的系数是0.157,t值是2.315,显著性是0.049。所以,两个结果都是显著的。
综上所述,通过以上的简单线性回归分析可知,可以认为通货膨胀和失业的替代关系在我国并不存在。
(获取更多知识,前往gz号程式解说)
原文来自https://mp.weixin.qq.com/s/aQaG8e7aix4DR9pvokP_uQ

文章来源:https://uudwc.com/A/MOg
文章来源地址https://uudwc.com/A/MOg

