剪枝技巧：
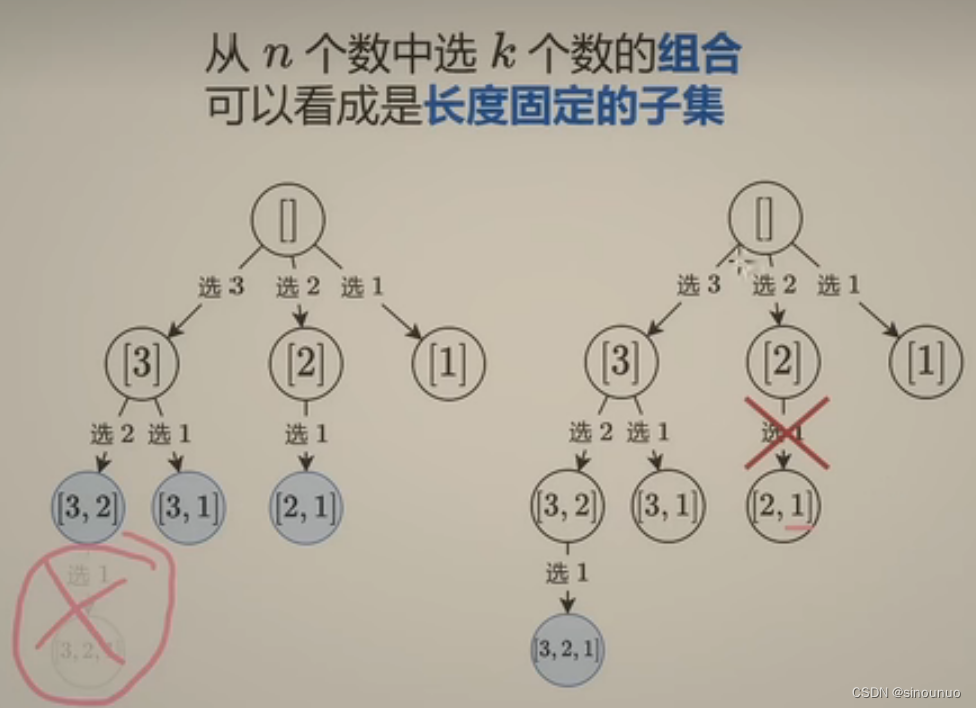
思路：剪枝的特点是找特定长度的子集。首先确定大框架，当path的长度等于k的时候，就要更新答案并且return。然后在进行path的元素选择，这里采用倒叙，从i到d（d=k-len(path)）倒着加入path中。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
path = []
ans = []
def dfs(i):
d = k - len(path)
# if i < d:
# return
if len(path) == k:
ans.append(path.copy())
return
for j in range(i,d-1,-1):
path.append(j)
dfs(j-1)
path.pop()
dfs(n)
return ans
思路：首先在[1,9]中选出不同的k个元素的子集，如果sum(path)==n,就更新答案。其余都是剪枝的套路代码。
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
nums = [i for i in range(1,10)]
ans = []
path = []
def dfs(i):
d = k - len(path)
if len(path) == k:
if sum(path) == n:
ans.append(path.copy())
return
for j in range(i,d-1,-1):
path.append(j)
dfs(j-1)
path.pop()
dfs(len(nums)) #传入子集的总的区间长度
return ans
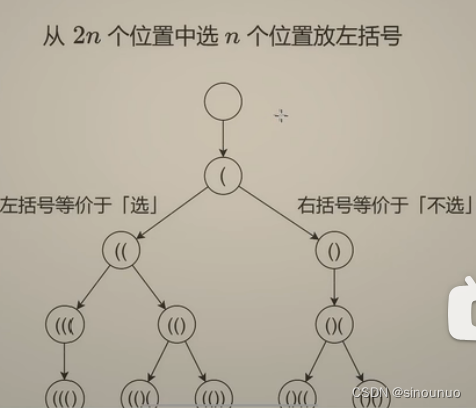
思路：相当于从2n个位置上，选择n个位置放置左括号，但是左右括号是有约束的，左括号不能超过n，右括号不能超过左括号。当把这2n个位置填完，就更新答案。因为左括号的个数也是约束条件，所以和函数一起递归。
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
#可以看成2n个位置上，选择(填入还是选择)填入
ans = []
m = n*2
path = ['']*m
def dfs(i,numofleft):
if i == m:
ans.append(''.join(path))
return
if numofleft < n:#左括号最大是n
path[i] = '('
dfs(i+1,numofleft+1)
if i - numofleft < numofleft: #右括号的个数不能超过左括号
path[i] = ')'
dfs(i+1,numofleft)
dfs(0,0)
return ans
思路：在每一个位置上，选择一个数填入，但是该数和前面的数不能相同，维护一个s，来存放当前可以选的数字，每次加入path之后，就把该数字减去。
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
ans = []
path = []
n = len(nums)
def dfs(i,s):
if i == n:
ans.append(path.copy())
return
for x in s:
path.append(x)
dfs(i+1,s-{x})
path.pop()
dfs(0,set(nums))
return ans
或者维护一个是否在路径中的list，当list中相应的位置是Fasle,就输入path，然后恢复现场。
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
ans = []
path = []
n = len(nums)
on_path = [False]*n
def dfs(i):
if i == n:
ans.append(path.copy())
return
for j in range(n):
if not on_path[j]:
path.append(nums[j])
on_path[j] = True
dfs(i+1)
on_path[j] = False #恢复现场
path.pop() #恢复现场
dfs(0)
return ans
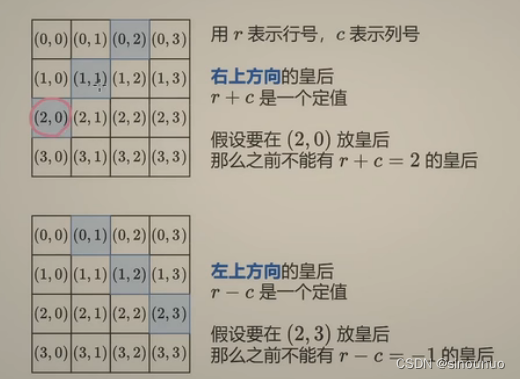
思路：皇后要在每一行都放置一个，那我们来递归行数，正确答案就应该是确定的一个列的顺序。之前的path就相当于cols，用全排列的方式，将行数和可以选择的列传入递归中。有两个点：
第一如何构造答案：在cols之前，有cols个. 在其之后有(n-1-cols)个.中间再拼接上Q。
第二是如何避免对角线打架：因为我们是按照从上到下的行数来放置的，所以只需要考虑左上方和右上方的数据，左上方和皇后位置的行列和一致，右上方和皇后位置的行列差一致。计算当前行列和、行列差，与cols中已经有的行列和、行列差对比。
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
#每一行都要放置一个皇后，那就在于，这个列的排序
ans = []
cols = [0]*n
def dfs(i,s):#把行数和当前可以选择的列传进去
if i == n:
ans.append(['.'*c + 'Q'+'.'*(n-1-c) for c in cols]) #对于每一个结果，拼接ans
return
for j in s: #枚举列
if all( j+i != cols[I] + I and j-i != cols[I] - I for I in range(i)):#这里要保证不在一个对角线上，cols[I]就是有皇后的位置的列。
cols[i] = j
dfs(i+1,s-{j})
dfs(0,set(range(n)))
return ans
class Solution:
def removeInvalidParentheses(self, s: str):
ans = []
path = []
n = len(s)
res_length = -1
st = []
def dfs(i):
nonlocal res_length
if i == n:
if st == []: #栈空，有效字符串
if res_length == -1: #首次递归到的一定是最大长度的有效子集
res_length = len(''.join(path)) #更新最大长度
if len(''.join(path)) == res_length: #如果当前的path是最大长度，就加入答案
ans.append(''.join(path))
return
#剪枝，n-i是没有选的长度+len(path)选择的长度 如果小于最大子集，就直接剪枝。
if n - i + len(path) < res_length:
return
if s[i] not in '()': #字母直接加
path.append(s[i])
dfs(i+1)
path.pop()
else:
path.append(s[i]) #先记录路径（先选，尽最大可能选）
if s[i] == '(':
st.append(s[i]) #左括号入栈，然后递归
dfs(i+1)
st.pop() #恢复现场
if s[i] == ')' and len(st) > 0: #右括号而且栈不是空
last = st.pop() #出栈，然后递归
dfs(i+1)
st.append(last) #恢复现场
path.pop() #恢复现场
dfs(i+1) #不选
dfs(0)
return list(set(ans))文章来源：https://uudwc.com/A/N1Pg
文章来源地址https://uudwc.com/A/N1Pg
