特殊矩阵的压缩存储（对称矩阵，三角矩阵，对角矩阵，稀疏矩阵的顺序，链序存储，十字链表的建立）

特殊矩阵的压缩存储

压缩存储的定义：
若多个数据元素的值都相同，则只分配一个元素值的存储空间，且
零元素不占存储空间。
能够压缩的一些矩阵： 一些特殊矩阵，如：对称矩阵，对角矩阵，三角矩阵，稀疏矩阵等。 稀疏矩阵定义：
矩阵中非零元素的个数较少(一 般小于5%)

一、对称矩阵

特点：

在n×n的矩阵a中，a_ij=a_ji(1<=i,j<=n)

存储方法：

只存储下（或者上）三角（包括主对角线）的数据元素。共占用n(n+1)/2个元素空间 可以以行序为主序将元素存放在一个一维数组**sa[n(n+1)/2]**中。

二、三角矩阵

特点：

对角线以下（或者以上）的数据元素（不包括对角线）全部为常数c

存储方法：

重复元素c共享一个元素存储空间，共占用m(n+1)/2+1个元素 空间：sa[1…n(n+1)/2+1]

三、对角矩阵（带状矩阵）

特点：

在n×n的方阵中，所有非零元素都集中在以主对角线为中心的带状区域中，区域外的值全为0，则成为对角矩阵。常见的有三对角矩阵，五对角矩阵，七对角矩阵等。

例：三对角矩阵

a[k]=2+3(i-2)+(j-i-2)-1=2*i+j-3

存储方法

四、稀疏矩阵的存储

**稀疏矩阵：**设在m×n的矩阵中有t个非零元素。令x=t/(m×n)，当x<=0.05时称为稀疏矩阵

**三元组(i,j,a_ij)**唯一确定矩阵的一个非零元

**压缩存储原则：**存各非零元的值，行列位置和矩阵的行列数

稀疏矩阵的压缩存储方法——顺序存储结构

三元组顺序表

三元组顺序表又称有序的双下标法

三元组顺序表的优点：非零元在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算

三元组顺序表的缺点：**不能随机存取。**若按行号存取某一行中的非零元，则需重头开始进行查找。

顺序存储结构

typedef int ElemType;
//----------稀疏矩阵的三元组顺序表存储表示----------
#define MAXSIZE 12500	//假设非零元个数的最大值为12500
typedef struct {
	int i, j;	//该非零元的行下标和列下标
	ElemType e;
} Triple;

typedef struct {
	Triple data[MAXSIZE + 1];		//非零元三元组表，data[0]未用
	int mu, nu, tu;	//矩阵的行数，列数，和非零元的个数
} TSMatrix;

打印矩阵

void PrintfTSMatrix(TSMatrix X){
	//打印矩阵
	int m,n;
	m=X.mu;	//稀疏矩阵的行数
	n=X.nu;	//稀疏矩阵的列数
	int k=1;	//三元组数组的下标
	for(int i=0;i<m;i++){
		for(int j=0;j<n;j++){	//双层循环遍历稀疏矩阵
			if(i==X.data[k].i&&j==X.data[k].j){	//如果i和j能够匹配三元组的下标
				printf("%d\t",X.data[k].e);	//如果能够配对则输出三元组的非零元素的值
				k++;	//继续遍历三元组的元素
			}else{
				printf("0\t");	//如果没有匹配则代表该处位置是0
			}
		}
		printf("\n");
	}
}

求稀疏矩阵的转置矩阵

int TransposeSMatrix(TSMatrix M, TSMatrix &T) {
	//采用三元组表存储表示，求稀疏矩阵M的转置矩阵T
	T.mu = M.nu;
	T.nu = M.mu;
	T.tu = M.tu;
	int q,p;
	if (T.tu) {
		q = 1;
		for (int col = 1; col <= M.nu; ++col) {	//按M的列查找
			for (p = 1; p <= M.tu; ++p) {
				if (M.data[p].j == col) {
					T.data[q].i = M.data[p].j;
					T.data[q].j = M.data[p].i;
					T.data[q].e = M.data[p].e;
					++q;
				}
			}
		}
	}
	return 0;
}

求稀疏矩阵的转置矩阵（快速转置）

链接: 看这个好理解

//快速转置
int FastTransposeSMatrix(TSMatrix M, TSMatrix &T) {
	//采用三元组顺序表存储表示，求稀疏矩阵M的转置矩阵T
	T.mu = M.nu;
	T.nu = M.mu;
	T.tu = M.tu;
	int col, num[1000], cpot[1000];
	int p, q;
	if (T.tu) {
		for (col = 1; col <= M.nu; ++col)	num[col] = 0;
		for (int t = 1; t <= M.tu; ++t)	++num[M.data[t].j];	//求M中每一列含非零元个数
		cpot[1] = 1;	//Cpot[1]=1的用处是第一列的在新三元表T的第一个插入位置为1。Cpot[0]是留给储存三元表行列数和非零元个数的。
		for (col = 2; col <= M.tu; ++col)	cpot[col] = cpot[col - 1] + num[col - 1];	//求第col列中第一个非零元在b.data中的序号
		for (p = 1; p <= M.tu; ++p) {
			col = M.data[p].j;
			q = cpot[col];
			T.data[q].i = M.data[p].j;
			T.data[q].j = M.data[p].i;
			T.data[q].e = M.data[p].e;
			++cpot[col];
		}
	}
	return 0;
}

稀疏矩阵的链式存储结构：十字链表

优点：它能够灵活地插入因运算而产生的新的非零元素，删除因运算而产生的新的零元素，实现矩阵的各种运算。

在十字链表中，矩阵的每一个非零元素用一个结点表示，该结点除了(row,col,value)以外，还要有两个域： **right:**用于链接同一行中的下一个非零元素； **down:**用于链接同一列中的下一个非零元素；

十字链表中结点的结构示意图 ：

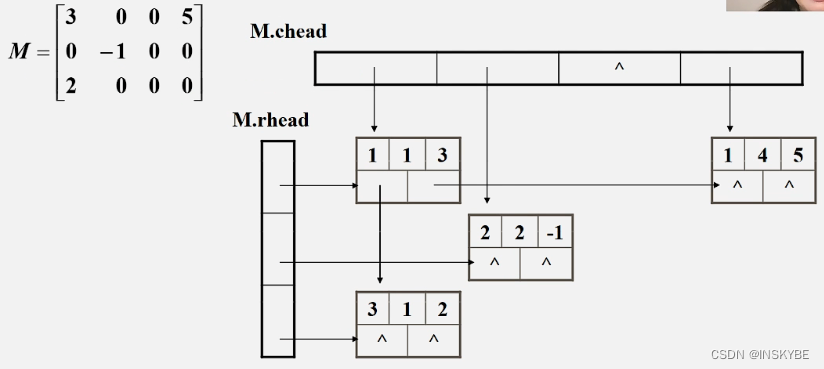
十字链表的建立

CrossList CreatSMatrix_OL(CrossList &M) {
	//创建稀疏矩阵M.采用十字链表存储表示
	int m, n, t;
	int i, j, e;
	OLink p, q;
	scanf("%d%d%d", &m, &n, &t);	//输入M的行数，列数和非零元个数
	M.mu = m;
	M.nu = n;
	M.tu = t;
	if (!(M.rhead = (OLink *)malloc((m + 1) * sizeof(OLink))))	exit(0);
	if (!(M.chead = (OLink *)malloc((n + 1) * sizeof(OLink))))	exit(0);
	for (i = 1; i <= m; i++)	M.rhead[i] = NULL;
	for (j = 1; j <= n; j++)   M.chead[j] = NULL;	//初始化行列头指针向量；各行列链表为空链表
	for (scanf("%d%d%d", &i, &j, &e);i!=0;scanf("%d%d%d",&i,&j,&e)) {
		if(!(p=(OLNode*)malloc(sizeof(OLNode)))){
			printf("初始化三元组失败"); exit(0);
		}
		p->i=i; p->j=j; p->e=e;	//生成结点
		if(NULL==M.rhead[i]||M.rhead[i]->j>j){	
			p->right=M.rhead[i];
			M.rhead[i]=p;
		}
		else{	//寻查在行表中的插入位置
			for(q=M.rhead[i];(q->down)&&q->right->j<j;q=q->right);
			p->right=q->right;	q->right=p;	//完成行插入	
			}
		if(NULL == M.chead[j] || M.chead[j]->i > i){
			p->down=M.chead[j];
			M.chead[j]=p;
		}
		else{	//寻查在列表中的插入位置
			for(q=M.chead[i];(q->down)&&q->down->i<i;q=q->down);
			p->down=q->down;
			q->down=p;
		}	
	}
	return M;
}

十字链表的完整代码

测试样例：

输入矩阵的行数、列数和非0元素个数：3 3 3
2 2 3
2 3 4
3 2 5
0 0 0
输出矩阵M:
2 2 3
3 2 5
2 3 4文章来源地址https://uudwc.com/A/R6398

#include<stdio.h>
#include<stdlib.h>
typedef struct OLNode {
	int i, j, e; //矩阵三元组i代表行 j代表列 e代表当前位置的数据
	struct OLNode *right, *down; //指针域 右指针 下指针
} OLNode, *OLink;
typedef struct {
	OLink *rhead, *chead; //行和列链表头指针
	int mu, nu, tu;  //矩阵的行数,列数和非零元的个数
} CrossList;
CrossList CreateMatrix_OL(CrossList M);
void display(CrossList M);
int main() {
	CrossList M;
	M.rhead = NULL;
	M.chead = NULL;
	M = CreateMatrix_OL(M);
	printf("输出矩阵M:\n");
	display(M);
	return 0;
}
CrossList CreateMatrix_OL(CrossList M) {
	int m, n, t;
	int i, j, e;
	OLNode *p, *q;
	printf("输入矩阵的行数、列数和非0元素个数：");
	scanf("%d%d%d", &m, &n, &t);
	M.mu = m;
	M.nu = n;
	M.tu = t;
	if (!(M.rhead = (OLink*)malloc((m + 1) * sizeof(OLink))) || !(M.chead = (OLink*)malloc((n + 1) * sizeof(OLink)))) {
		printf("初始化矩阵失败");
		exit(0);
	}
	for (i = 1; i <= m; i++) {
		M.rhead[i] = NULL;
	}
	for (j = 1; j <= n; j++) {
		M.chead[j] = NULL;
	}
	for (scanf("%d%d%d", &i, &j, &e); 0 != i; scanf("%d%d%d", &i, &j, &e)) {
		if (!(p = (OLNode*)malloc(sizeof(OLNode)))) {
			printf("初始化三元组失败");
			exit(0);
		}
		p->i = i;
		p->j = j;
		p->e = e;
		//链接到行的指定位置
		if (NULL == M.rhead[i] || M.rhead[i]->j > j) {
			p->right = M.rhead[i];
			M.rhead[i] = p;
		} else {
			for (q = M.rhead[i]; (q->right) && q->right->j < j; q = q->right);
			p->right = q->right;
			q->right = p;
		}
		//链接到列的指定位置
		if (NULL == M.chead[j] || M.chead[j]->i > i) {
			p->down = M.chead[j];
			M.chead[j] = p;
		} else {
			for (q = M.chead[j]; (q->down) && q->down->i < i; q = q->down);
			p->down = q->down;
			q->down = p;
		}
	}
	return M;
}
void display(CrossList M) {
	for (int i = 1; i <= M.nu; i++) {
		if (NULL != M.chead[i]) {
			OLink p = M.chead[i];
			while (NULL != p) {
				printf("%d\t%d\t%d\n", p->i, p->j, p->e);
				p = p->down;
			}
		}
	}
}