文章来源地址https://uudwc.com/A/Rmqo
前言
- 几何分布,和超几何分布,听名字很像
- 但实际上这两种随机变量,没有任何关系
文章来源:https://uudwc.com/A/Rmqo
1 什么是几何分布
- 一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。
- 详细地说,是:前k-1次皆失败,第k次成功的概率。
- 首先几何分布,属于古典概型/ 伯努利试验,特点是:只有每次试验只可能有两种结果
- 如果只做1次试验,那是属于0-1分布
- 如果做N次试验,但是只有最后一次成功,则随机变量符合 几何分布
- 如果做N次试验,没其他限制,则随机变量符合 二项分布
- 由上可知,0-1分布,几何分布,应该都可以归纳为,二项分布的一种特例。
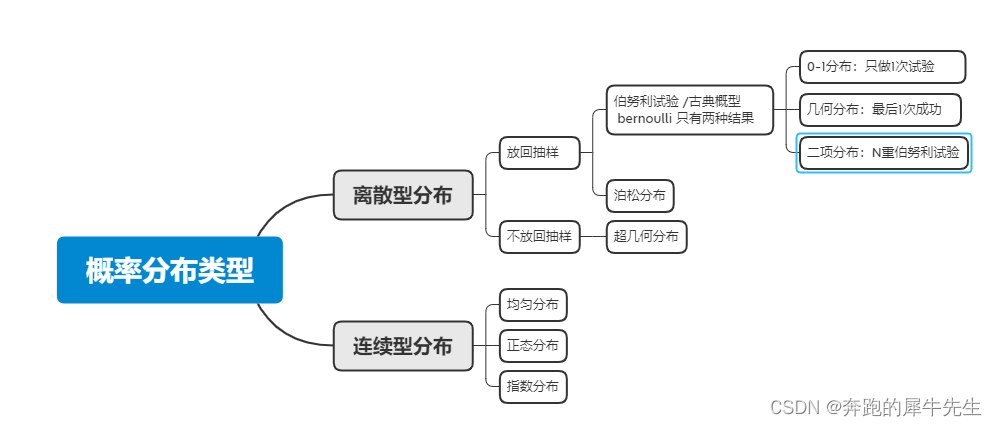
2 几何分布在概率分布中的定位
图上有错,伯努利试验 和古典概型不一样
古典概率,只强调所有事件概率相等,并不要求每次试验概率稳定
3 几何分布的公式
几何分布的公式
- 在伯努利试验中,成功的概率为p
- 若ξ表示出现首次成功时的试验次数,则ξ是离散型随机变量
- 它只取正整数,且有P(ξ=k)=(1-p)的(k-1)次方乘以p (k=1,2,…,0<p<1),此时称随机变量ξ服从几何分布。
- 也就是 P(ξ=k)=(1-p)^(k-1) *p
- 它的期望为1/p,方差为(1-p)/(p的平方)。
4 为什么叫几何分布
- 几何分布 P(ξ=k)=(1-p)^(k-1) *p
- 就是因为分布的各项,都是等比数列!
- 就是因为分布的各项,中间项都是前后两项的几何平均数,所以叫几何分布!
4.1 先需要了解算术平均数和几何平均数
- 首先要了解
- a和b的算术平均数是 (a+b)/2
- a和b的几何平均数 (a*b)^-2 或者说 √ab
4.2 第1:几何布分布的,各个项之间,就是等比数据,公比为 (1-p )
- 几何分布 P(ξ=k)=(1-p)^(k-1) *p
- p*(1-p),p*(1-p)^2 ,p*(1-p)^3
- 公比都是 (1-p)
4.3 第2:几何布分布每个中间的项,都是前后两个数的几何平均数,因此得名
- 几何布分布的,每个中间的项,都是前后两个数的几何平均数
- 因此叫做 几何分布
- p*(1-p),p*(1-p)^2 ,p*(1-p)^3
- p*(1-p)*p*(1-p)^3 =p^2*(1-p)^4 = (p*(1-p)^2 )^2
5 几何分布的期望
- 一般意义的几何分布所说的期望,默认是指,几何期望的定义:伯努利试验,最后一次成功,成功次数n对应的随机变量的期望。
- 而实际上,也可以在二项分布下其他随机变量的数学期望,比如,失败次数m (m=n-1)的数学期望,
- 这个期望显然和n的数学期望是不同的!
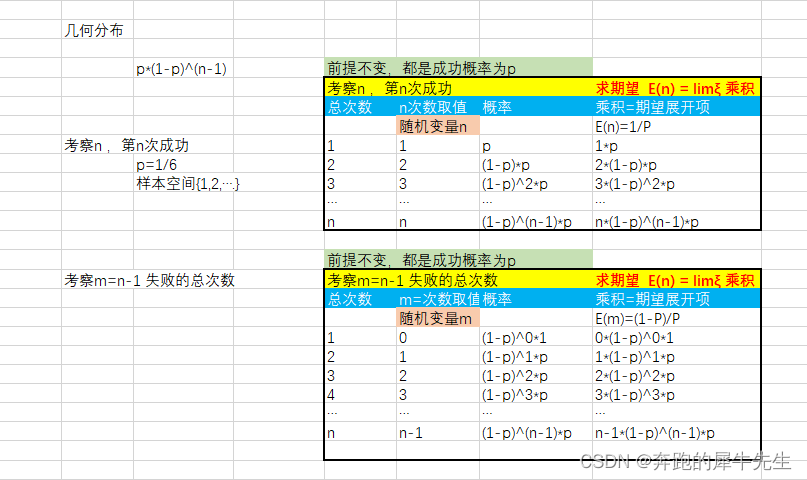
5.1 几何分布变量 n的期望
- 如果我们定义的随机变量是 n
- n 表示n次伯努利试验,最后1次成功
- 成功概率为p
- 那么,n的数学期望 E(n) =1/p
| 前提不变,都是成功概率为p | |||
| 考察n ,第n次成功 | 求期望 E(n) = limξ 乘积 | ||
| 总次数 | n次数取值 | 概率 | 乘积=期望展开项 |
| 随机变量n | E(n)=1/P | ||
| 1 | 1 | p | 1*p |
| 2 | 2 | (1-p)*p | 2*(1-p)*p |
| 3 | 3 | (1-p)^2*p | 3*(1-p)^2*p |
| … | … | … | … |
| n | n | (1-p)^(n-1)*p | n*(1-p)^(n-1)*p |
- 下面是推导过程
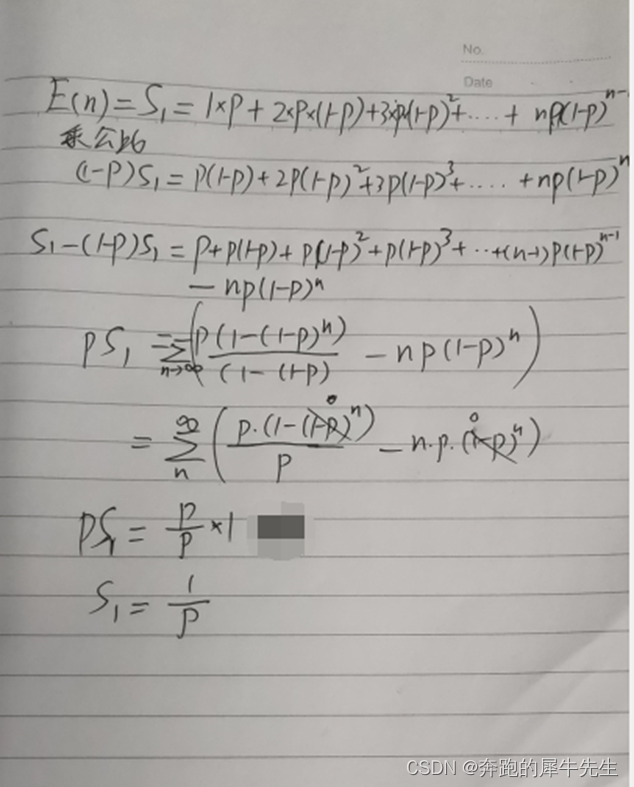
5.2 几何分布,其中失败次数 m的期望
- 如果我们定义的随机变量是 n
- n 表示n次伯努利试验,最后1次成功,那么失败次数为m , m=n-1
- 成功概率为p ,失败概率是1-p
- 那么, 失败次数m的数学期望 E(m) =(1-p)/p
| 前提不变,都是成功概率为p | |||
| 考察m=n-1 失败的总次数 | 求期望 E(n) = limξ 乘积 | ||
| 总次数 | m=次数取值 | 概率 | 乘积=期望展开项 |
| 随机变量m | E(m)=(1-P)/P | ||
| 1 | 0 | (1-p)^0*1 | 0*(1-p)^0*1 |
| 2 | 1 | (1-p)^1*p | 1*(1-p)^1*p |
| 3 | 2 | (1-p)^2*p | 2*(1-p)^2*p |
| 4 | 3 | (1-p)^3*p | 3*(1-p)^3*p |
| … | … | … | … |
| n | n-1 | (1-p)^(n-1)*p | n-1*(1-p)^(n-1)*p |
- 下面是推导过程

6 几何分布的方差
几何分布的方差,第n次成功,n的方差为 (1-p)/p^2
推导过程暂缺


7 几何分布的概率分布:分布率,分布函数,分布图
- 默认集合分布的随机变量,都是指最后一次成功的次数n 所对应的随机变量
- 如果要求几何分布的失败次数m (m=n-1) 一般需要单独指明
7.1 几何分布的分布律
- 几何分布的概率分布率是
- 可以如下表格表示
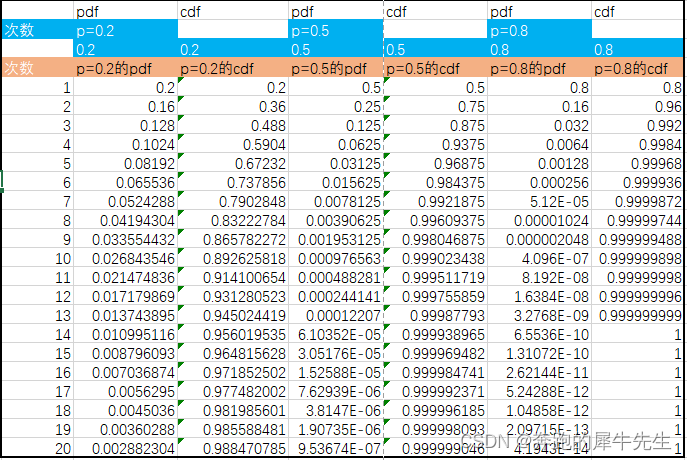
7.2 几何分布的概率分布函数
- 因为这个有通项
- 所以概率分布函数比较简洁
- p(n) = p*(1-p)^(n-1)
7.3 几何分布的概率分布图形
- cdf
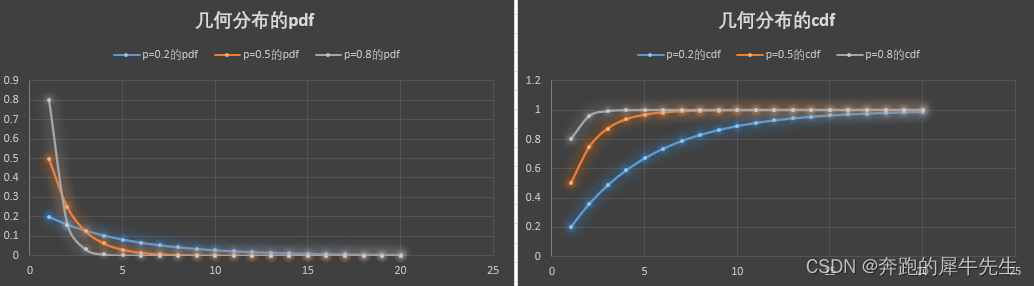
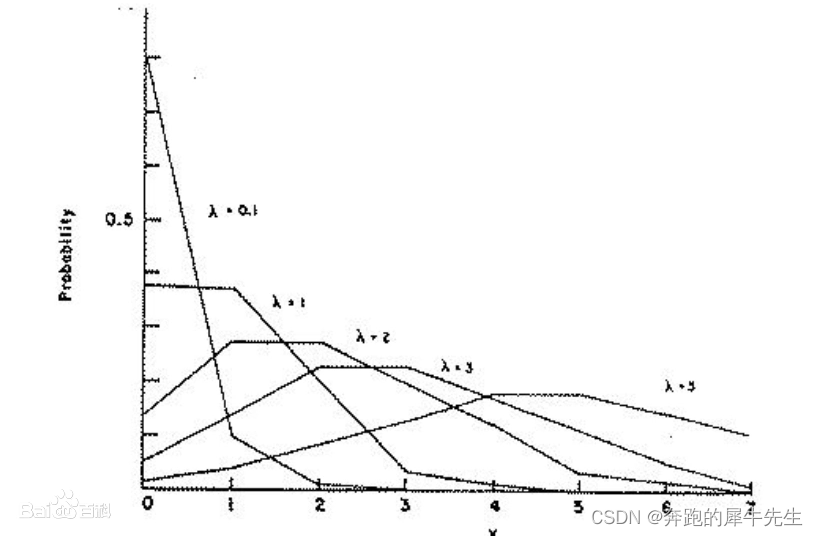
百度百科,几何分布的图形有这么多。。。还需要了解
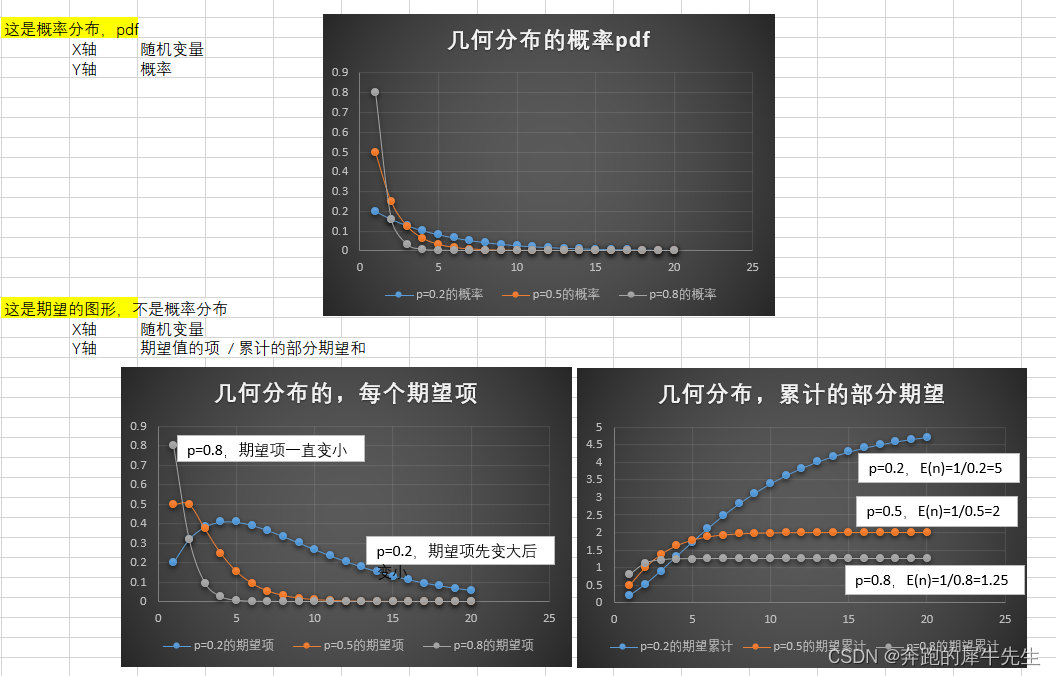
8 几何分布的 期望的图形(一般很少画期望的图形)
- 几何分布的期望公式
- E(n)= n*p*(1-p)^(n-1)
- 可见,几何分布,当概率p 越小,总期望最后1次成功的概率,则n会越大
- 比如概率 0.8的时候,期望1.25次就可以成功
- 而概率为0.2的时候,期望5次才可以成功
- 符合直觉
- 另外,其实假设试验次数无限次,期望次数= 1/P , 符合这样的规律?
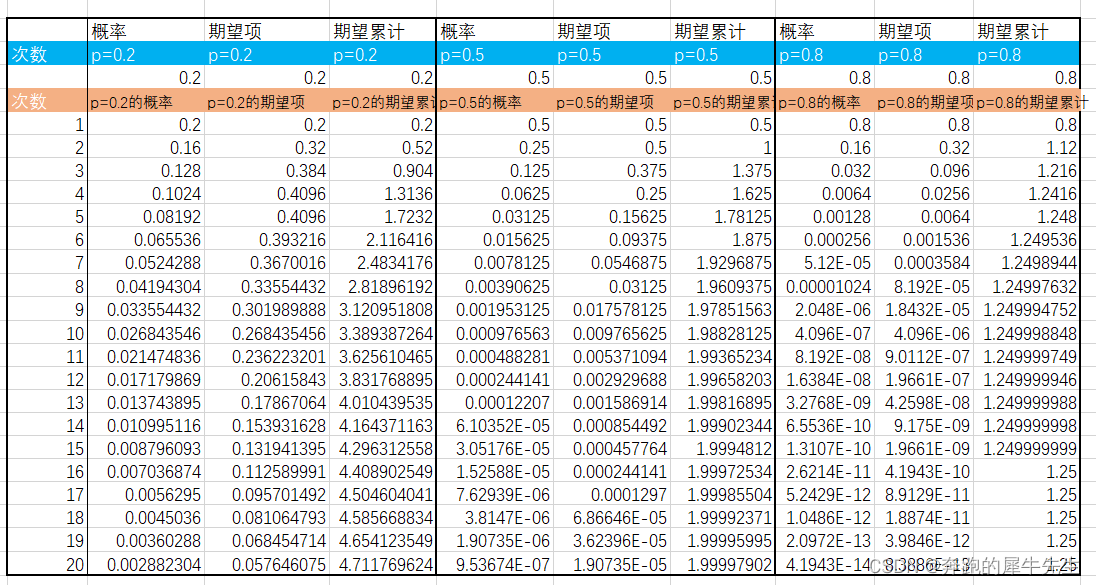
- 下图
- 左1是,期望的每个项的数值的图示
- 左2是,累计的前面部分 期望项的和,逐渐接近整体的期望 ,模拟近似 期望E(n)