线性代数（8）：特征值、特征向量和相似矩阵

一、特征值和特征向量

（2）定义

        有矩阵 A 为 n 阶矩阵，Ax = λx （ λ 为一个实数，x为 n 维非零列向量 ），则称 λ 为方阵 A 的特征值， x 为特征向量；

（2）求解

1.2.1 公式

        求特征值：使 | A - λE | = 0，其解的 λ 值即为矩阵 A 的特征值；

文章来源地址https://uudwc.com/A/WY6va

        求特征向量： 使 ( A - λE )x = 0,设 x 为与 A 具有相同行数的列向量，将求得的 λ 值代入，求得的解系与任意常数相乘，即为特征向量；

 1.2.2 

         例：

        解：

二、相似

（1）定义

        P^(-1) * AP = B ;（ A、B 为 n 阶方阵，P 为可逆矩阵 ）

        称其 B 为 A 的相似矩阵

（2）特性

        （1）A 和 B 有相同的特征多项式与特征值；

        （2）| A | = | B | ；

        （3）R( A ) = R( B )  ；

        （4） A^m 和 B^m 也相似 ；（ m 为正整数 ）

（3）

        例： 

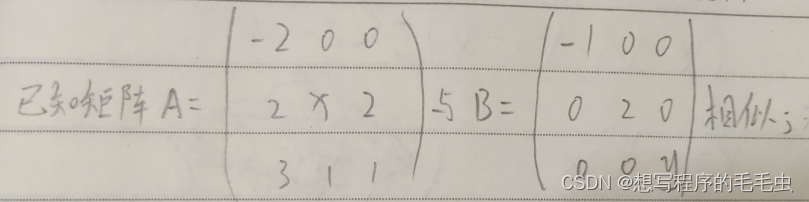
        ① 求 x 和 y ；

        解： 

        ②求一个可逆 P 使得 P^(-1) * AP = B ;

        解：