对于一棵多叉树,我们可以通过 “左孩子右兄弟” 表示法,将其转化成一棵二叉树。
如果我们认为每个结点的子结点是无序的,那么得到的二叉树可能不唯一。
换句话说,每个结点可以选任意子结点作为左孩子,并按任意顺序连接右兄弟。
给定一棵包含 N 个结点的多叉树,结点从 1 至 N 编号,其中 1 号结点是根,每个结点的父结点的编号比自己的编号小。
请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树,高度最高是多少。
注:只有根结点这一个结点的树高度为 0。
例如如下的多叉树:
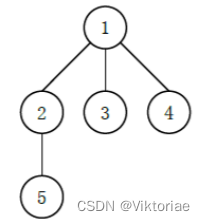
可能有以下 3 种 (这里只列出 3 种,并不是全部) 不同的 “左孩子右兄弟”表示:
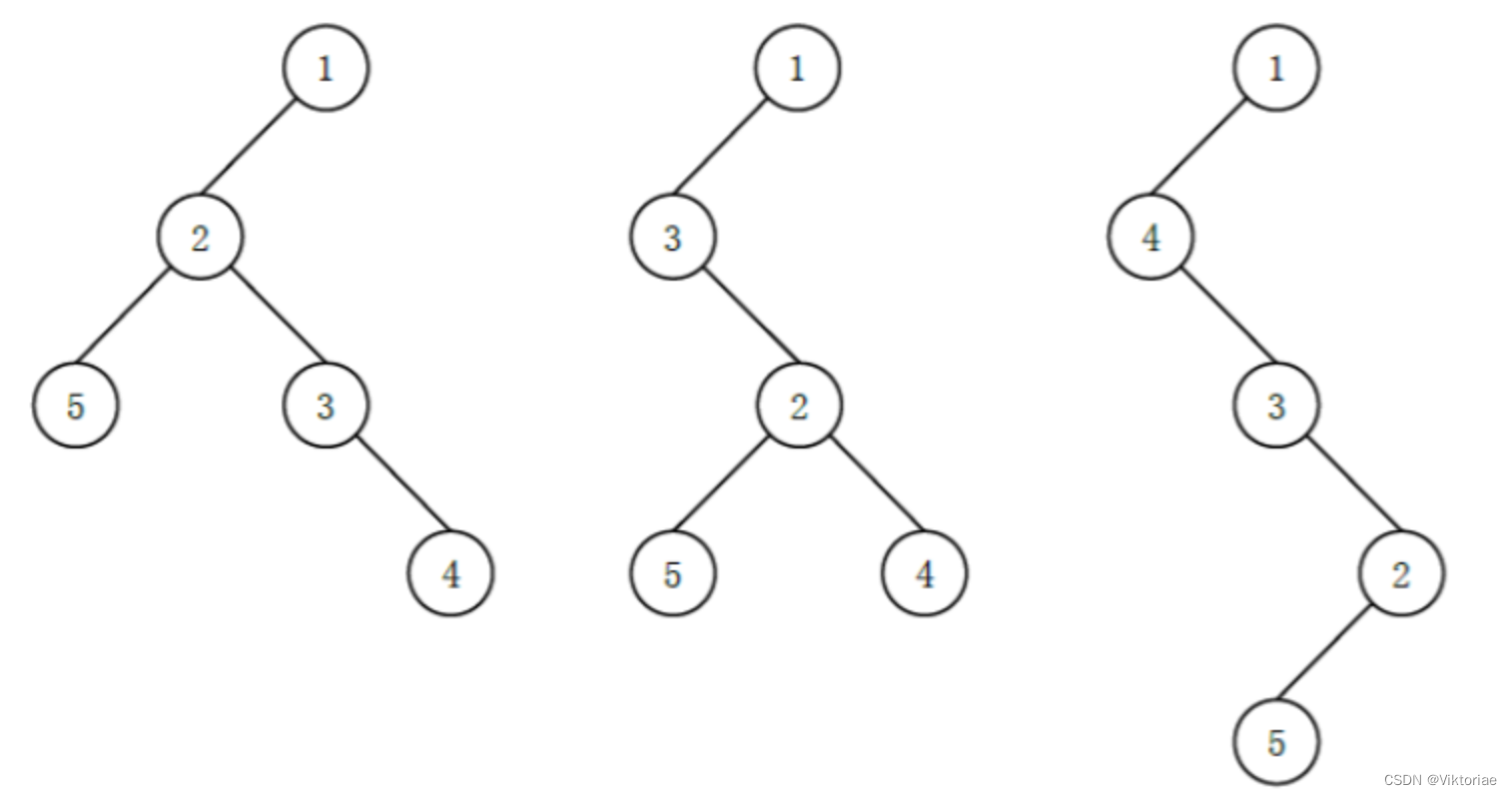
其中最后一种高度最高,为 4。
输入格式
输入的第一行包含一个整数 N。
以下 N−1 行,每行包含一个整数,依次表示 2 至 N 号结点的父结点编号。
输出格式
输出一个整数表示答案。
数据范围
对于 30% 的评测用例,1≤N≤20;
对于所有评测用例,1≤N≤105。
输入样例:
5
1
1
1
2
输出样例:
4文章来源:https://uudwc.com/A/XE5Z
思路 :文章来源地址https://uudwc.com/A/XE5Z
- 求树的高度,从最下往上看,动态规划,需要递归访问子树
- 状态表示:f[u]表示以u为根结点的子树的最大高度
- 状态计算:f[u] = max(f[u], f[v] + num[u])
即,当前树的高度等于它 与 其子树的高度+以这个节点为根的儿子结点数量 取max
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int n;
int e[N], ne[N], h[N], idx;
int num[N], f[N];
void add(int u, int v) {
e[idx] = v; ne[idx] = h[u]; h[u] = idx ++ ;
}
void dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
dfs(j);
f[u] = max(f[u], f[j] + num[u]);
}
}
int main() {
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 2, x; i <= n; ++ i) {
scanf("%d", &x);
add(x, i);
num[x] ++ ;
}
dfs(1);
printf("%d", f[1]);
}