智能优化算法:金豺优化算法
1.金豺优化算法简介
金豺优化(Golden jackal optimization,GJO)算法是2022年提出的一种新的元启发式算法,该算法是一种模仿金豺的合作狩猎行为的新型智能优化算法。GJO算法包括三个基本步骤是搜索猎物、包围猎物和攻击猎物。
2.金豺优化算法基本原理
2.1灵感来源
金豺狩猎过程主要分为三个基本阶段:
(1)搜索猎物,并逼近猎物;
(2)包围猎物,并刺激猎物直到它们停止运动;
(3)攻击猎物。
2.2 数学模型与算法
2.2.1 搜索空间模型
金豺种群初始化数学描述如下:
Y
0
=
Y
min
+
rand
×
(
Y
max
−
Y
min
)
(1)
Y_{0}=Y_{\min }+\operatorname{rand} \times\left(Y_{\max }-Y_{\min }\right) \tag{1}
Y0=Ymin+rand×(Ymax−Ymin)(1)
式中:
Y
0
Y_0
Y0为初始金豺种群的位置;是
r
a
n
d
rand
rand[0,1]范围内的随机数;
Y
m
a
x
Y_{max}
Ymax和
Y
m
i
n
Y_{min}
Ymin分别是求解问题的上下边界。
在GJO算法中,猎物矩阵表示为:
Prey
=
[
Y
1
,
1
⋯
Y
1
,
j
⋯
Y
1
,
d
⋮
⋱
⋮
⋮
Y
i
,
1
⋯
Y
i
,
j
⋯
Y
i
,
d
⋮
⋮
⋱
⋮
Y
n
,
1
⋯
Y
n
,
j
⋯
Y
n
,
d
]
(2)
\text { Prey }=\left[\begin{array}{ccccc} Y_{1,1} & \cdots & Y_{1, j} & \cdots & Y_{1, d} \\ \vdots & \ddots & \vdots & & \vdots \\ Y_{i, 1} & \cdots & Y_{i, j} & \cdots & Y_{i, d} \\ \vdots & & \vdots & \ddots & \vdots \\ Y_{n, 1} & \cdots & Y_{n, j} & \cdots & Y_{n, d} \end{array}\right] \tag{2}
Prey =⎣⎢⎢⎢⎢⎢⎢⎡Y1,1⋮Yi,1⋮Yn,1⋯⋱⋯⋯Y1,j⋮Yi,j⋮Yn,j⋯⋯⋱⋯Y1,d⋮Yi,d⋮Yn,d⎦⎥⎥⎥⎥⎥⎥⎤(2)
式中: P r e y Prey Prey为猎物矩阵; Y i , j Y_{i,j} Yi,j为第 i i i个猎物的第 j j j维位置;中第1和 P r e y Prey Prey第2的胜者一起作为豺狼对;n为猎物的数量;d为问题求解的维度。
在优化过程中,采用适应度(目标)函数估计每个猎物的适应度值,所有猎物的适应度值矩阵表示如下:
F
O
A
=
[
f
(
Y
1
,
1
;
Y
1
,
2
;
⋯
;
Y
1
,
d
)
f
(
Y
2
,
1
;
Y
2
,
1
;
⋯
;
Y
2
,
d
)
⋮
f
(
Y
n
,
1
;
Y
n
,
2
;
⋯
;
Y
n
,
d
)
]
(3)
F_{O A}=\left[\begin{array}{c} f\left(Y_{1,1} ; Y_{1,2} ; \cdots ; Y_{1, d}\right) \\ f\left(Y_{2,1} ; Y_{2,1} ; \cdots ; Y_{2, d}\right) \\ \vdots \\ f\left(Y_{n, 1} ; Y_{n, 2} ; \cdots ; Y_{n, d}\right) \end{array}\right] \tag{3}
FOA=⎣⎢⎢⎢⎡f(Y1,1;Y1,2;⋯;Y1,d)f(Y2,1;Y2,1;⋯;Y2,d)⋮f(Yn,1;Yn,2;⋯;Yn,d)⎦⎥⎥⎥⎤(3)
式中: F O A F_{OA} FOA为猎物的适应度值矩阵; f ( ) f() f()为适应度函数或目标函数;适应度值最优的作为雄豺,适应度值次优的作为雌豺。豺狼对得到相应猎物的位置。
2.2.2 搜索猎物(勘探阶段)
正如豺狼的本性,它们知道如何感知并跟随猎物,但偶尔猎物不会轻易被抓住从而逃脱。因此,豺狼就会等待和寻找其他的猎物。狩猎工作由雄性豺狼领导。雌性豺狼跟随雄性豺狼。
Y
1
(
t
)
=
Y
M
(
t
)
−
E
⋅
∣
Y
M
(
t
)
−
r
l
⋅
Prey
(
t
)
∣
(4)
Y_{1}(t)=Y_{M}(t)-E \cdot\left|Y_{M}(t)-r l \cdot \operatorname{Prey}(t)\right| \tag{4}
Y1(t)=YM(t)−E⋅∣YM(t)−rl⋅Prey(t)∣(4)
Y 2 ( t ) = Y F M ( t ) − E ⋅ ∣ Y F M ( t ) − r l ⋅ Prey ( t ) ∣ (5) Y_{2}(t)=Y_{F M}(t)-E \cdot\left|Y_{F M}(t)-r l \cdot \operatorname{Prey}(t)\right| \tag{5} Y2(t)=YFM(t)−E⋅∣YFM(t)−rl⋅Prey(t)∣(5)
式中: t t t为当前迭代次数; P r e y ( t ) Prey(t) Prey(t)为第 t t t次迭代的猎物的位置; Y M ( t ) , Y F M ( t ) Y_M(t),Y_{FM}(t) YM(t),YFM(t)分别为第 t t t次迭代的雄性豺狼和雌性豺狼的位置; Y 1 ( t ) , Y 2 ( t ) Y_1(t),Y_2(t) Y1(t),Y2(t)分别为第 t t t次迭代的与猎物相应的雄性豺狼和雌性豺狼更新后的位置。
E
E
E为猎物的逃脱能量,可用如下公式计算:
E
=
E
1
∗
E
0
(6)
E=E1*E_0 \tag{6}
E=E1∗E0(6)
E
1
E_1
E1表示猎物能量的下降过程,
E
0
E_0
E0表示猎物能量的初始状态。
E
0
=
2
∗
r
−
1
(7)
E_0=2*r-1 \tag{7}
E0=2∗r−1(7)
式中:r为[0,1]范围内的随机数。
E
1
=
c
1
∗
(
1
−
(
t
/
T
)
)
(8)
E_1=c_1*(1-(t/T))\tag{8}
E1=c1∗(1−(t/T))(8)
式中:
T
T
T为最大迭代次数;
c
1
c_1
c1为一个常数,取值为1.5;
t
t
t为当前迭代次数。在整个迭代过程中,
E
1
E_1
E1从1.5线性减少到0。
在公式(4)和(5)中,
r
l
rl
rl表示一个基于莱维分布的随机数,可用如下公式计算:
r
l
=
0.05
∗
L
F
(
y
)
(9)
rl=0.05*LF(y)\tag{9}
rl=0.05∗LF(y)(9)
L
F
(
)
LF()
LF()是莱维飞行函数,其计算方法如下:
L
F
(
y
)
=
0.01
×
(
μ
×
σ
)
/
(
∣
v
(
1
/
β
)
∣
)
;
σ
=
(
Γ
(
1
+
β
)
×
sin
(
π
β
/
2
)
Γ
(
1
+
β
2
)
×
β
×
(
2
β
−
1
2
)
)
1
/
β
(10)
L F(y)=0.01 \times(\mu \times \sigma) /\left(\left|v^{(1 / \beta)}\right|\right) ; \sigma=\left(\frac{\Gamma(1+\beta) \times \sin (\pi \beta / 2)}{\Gamma\left(\frac{1+\beta}{2}\right) \times \beta \times\left(2^{\frac{\beta-1}{2}}\right)}\right)^{1 / \beta}\tag{10}
LF(y)=0.01×(μ×σ)/(∣∣∣v(1/β)∣∣∣);σ=⎝⎛Γ(21+β)×β×(22β−1)Γ(1+β)×sin(πβ/2)⎠⎞1/β(10)
式中:
μ
\mu
μ和
v
v
v为(0,1)范围内的随机数;
β
\beta
β为一个默认常数,取值为1.5。
综上,豺狼的位置更新公式如下:
Y
(
t
+
1
)
=
Y
1
(
t
)
+
Y
2
(
t
)
2
(11)
Y(t+1)=\frac{Y_{1}(t)+Y_{2}(t)}{2} \tag{11}
Y(t+1)=2Y1(t)+Y2(t)(11)
式中: Y ( t + 1 ) Y(t+1) Y(t+1)为第t+1次迭代后的豺狼的位置。
2.2.3 包围并攻击猎物(开发阶段)
当猎物被豺狼侵扰时,它们的逃脱能量会减少,然后豺狼对会将在前一阶段检测到的猎物包围起来。当豺狼对将猎物包围后,开始攻击并吞食猎物。雄性和雌性豺狼一起捕猎的行为的数学模型如下:
Y
1
(
t
)
=
Y
M
(
t
)
−
E
⋅
∣
r
l
⋅
Y
M
(
t
)
−
Prey
(
t
)
∣
(12)
Y_{1}(t)=Y_{M}(t)-E \cdot\left|r l \cdot Y_{M}(t)-\operatorname{Prey}(t)\right| \tag{12}
Y1(t)=YM(t)−E⋅∣rl⋅YM(t)−Prey(t)∣(12)
Y 2 ( t ) = Y F M ( t ) − E ⋅ ∣ r l ⋅ Y F M ( t ) − Prey ( t ) ∣ (13) Y_{2}(t)=Y_{F M}(t)-E \cdot\left|r l \cdot Y_{F M}(t)-\operatorname{Prey}(t)\right| \tag{13} Y2(t)=YFM(t)−E⋅∣rl⋅YFM(t)−Prey(t)∣(13)
式中: t t t为当前迭代次数; P r e y ( t ) Prey(t) Prey(t)为第 t t t次迭代的猎物的位置; Y M ( t ) , Y F M ( t ) Y_M(t),Y_{FM}(t) YM(t),YFM(t)分别为第 t t t次迭代的雄性豺狼和雌性豺狼的位置;; Y 1 ( t ) , Y 2 ( t ) Y_1(t),Y_2(t) Y1(t),Y2(t)分别为第 t t t次迭代的与猎物相应的雄性豺狼和雌性豺狼更新后的位置。
最后,豺狼的位置更新仍然按照公式(11)计算。
算法伪代码如下:
3.实验结果
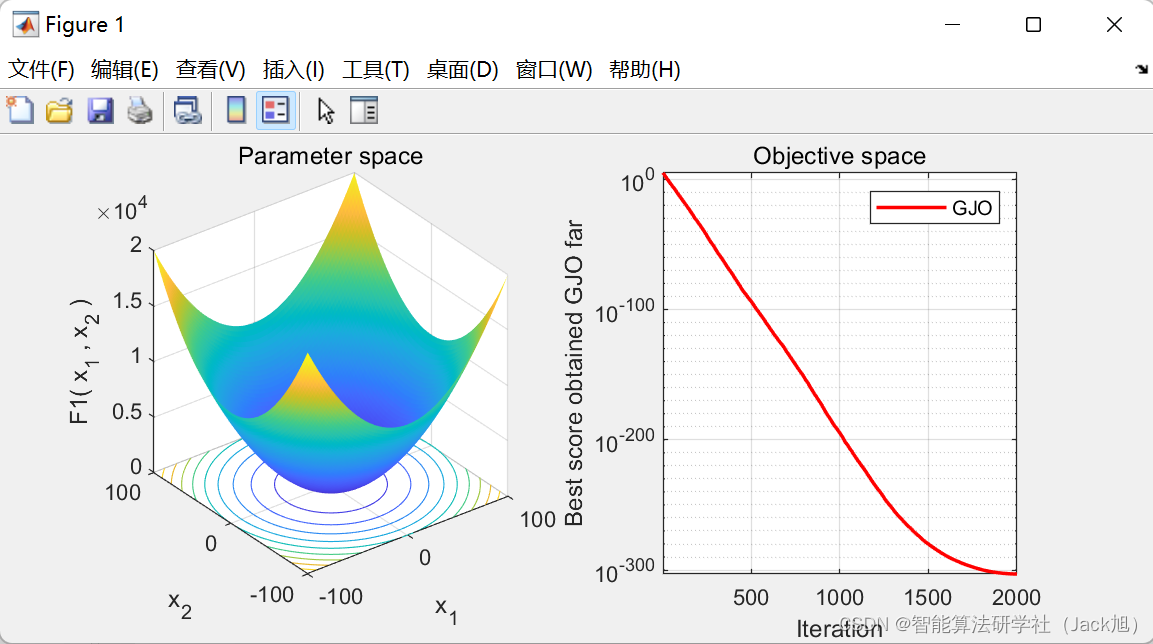 文章来源:https://uudwc.com/A/brER
文章来源:https://uudwc.com/A/brER
4.参考文献
[1] Nc A , Mma B . Golden Jackal Optimization: A Novel Nature-Inspired Optimizer for Engineering Applications. 2022.文章来源地址https://uudwc.com/A/brER