数据结构：有向完全图和无向完全图的边数

Kinght_123 • 2023年06月28日 10:00 • 2年前 • 编程日记 • 阅读(3) • 违法举报

一、无向完全图

一个拥有n个结点的无向完全图的边数为：n×(n−1)÷2

具体的解释：
比如我们有一个拥有4个结点的无向完全图，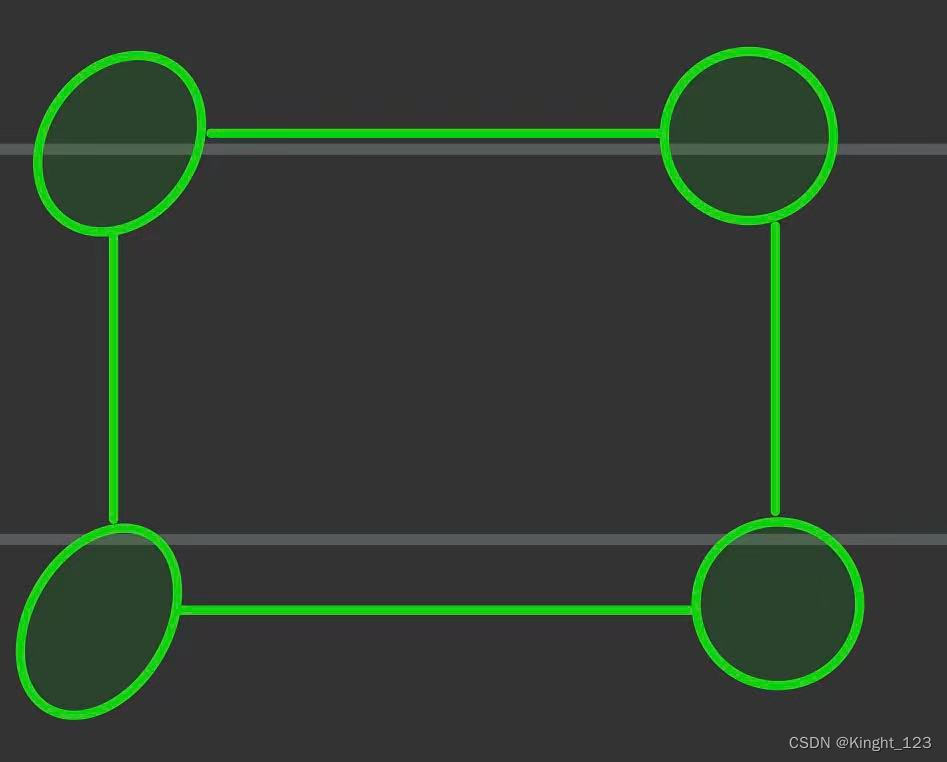
我们首尾依次连接，共有4条边。
然后我们选择其他的两条边来连线。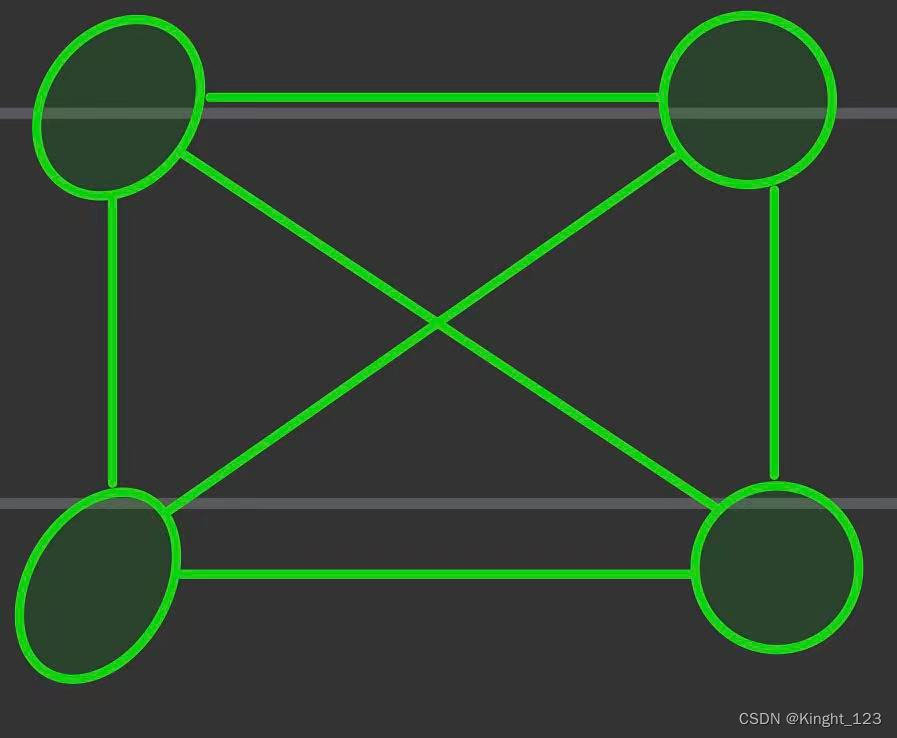

又多出了2条边。一共有4 + 2 = 6条边。
我们来分析一下具体的过程，首先如果为n个结点的话，首先首尾相连有n条边，然后选择其余的两条边来连线，边数为(n−1)÷2
所以无向完全图的边数为：n×(n−1)÷2

二、有向完全图

有向完全图与无向完全图的区别是，有向完全图的两个结点可以连接两条边。
那么结点为n的有向完全图的边数就为：n×(n−1)文章来源地址https://uudwc.com/A/gk3Lo

原文地址:https://blog.csdn.net/Kinght_123/article/details/125147426

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请联系站长进行投诉反馈，一经查实，立即删除！