机器学习—非零中心化、非零中心化会带来的问题

众所周知，激活函数最好具有关于零点对称的特性，不关于零点对称会导致收敛变慢。这种说法看到几次了，但对于背后的原因却一直比较模糊，今天就来捋一捋。

神经元模型

如图1所示是神经网络中一个典型的神经元设计，它完全仿照人类大脑中神经元之间传递数据的模式设计。大脑中，神经元通过若干树突（dendrite）的突触（synapse），接受其他神经元的轴突（axon）或树突传递来的消息，而后经过处理再由轴突输出。

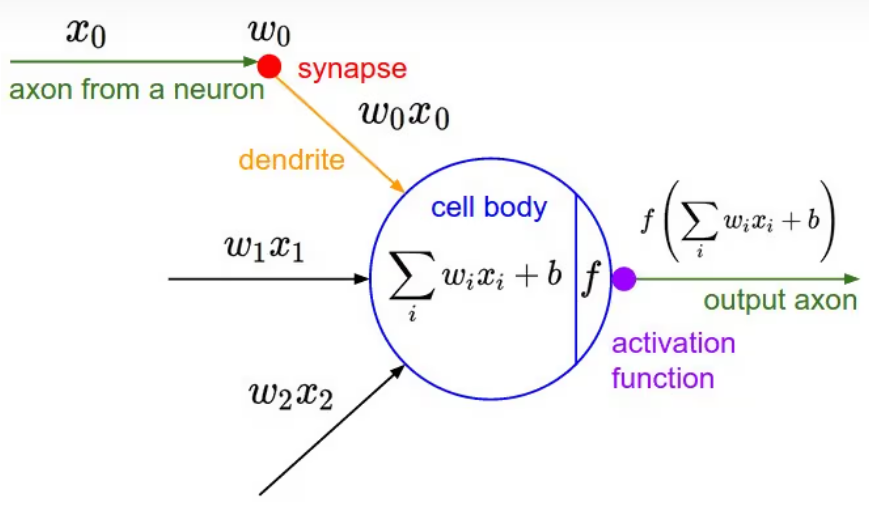
图1来自：聊一聊深度学习的activation function - 知乎

在图1中， xi 是其他神经元的轴突传来的消息， wi 是突触对消息的影响， wi*xi 则是神经元树突上传递的消息。这些消息经由神经元整合后再激活输出（ f(z) ）。这里，整合的过程是线性加权的过程，各输入特征 xi 之间没有相互作用。激活函数（active function）一般来说则是非线性的，各输入特征 xi 在此处相互作用。

Sigmoid 函数

Sigmodid 函数表达式： $\sigma(x)=\tfrac{1}{1+e^{-x}}$

Sigmoid函数是深度学习领域开始时使用频率最高的activation function。它是便于求导的平滑函数，其导数为 $\sigma (x)(1-\sigma(x))$ ，这是优点。然而，Sigmoid有三大缺点：

容易出现gradient vanishing
函数输出并不是zero-centered
幂运算相对来讲比较耗时

Gradient Vanishing

优化神经网络的方法是Back Propagation，即导数的后向传递：先计算输出层对应的loss，然后将loss以导数的形式不断向上一层网络传递，修正相应的参数，达到降低loss的目的。
Sigmoid函数在深度网络中常常会导致导数逐渐变为0，使得参数无法被更新，神经网络无法被优化。原因在于两点：
(1) 在上图中容易看出，当σ(x) 中 x 较大或较小时，导数接近0，而后向传递的数学依据是微积分求导的链式法则，当前层的导数需要之前各层导数的乘积，几个小数的相乘，结果会很接近0。
(2) Sigmoid导数的最大值是0.25，这意味着导数在每一层至少会被压缩为原来的1/4，通过两层后被变为1/16，…，通过10层后为1/1048576。请注意这里是“至少”，导数达到最大值这种情况还是很少见的。

输出不是zero-centered

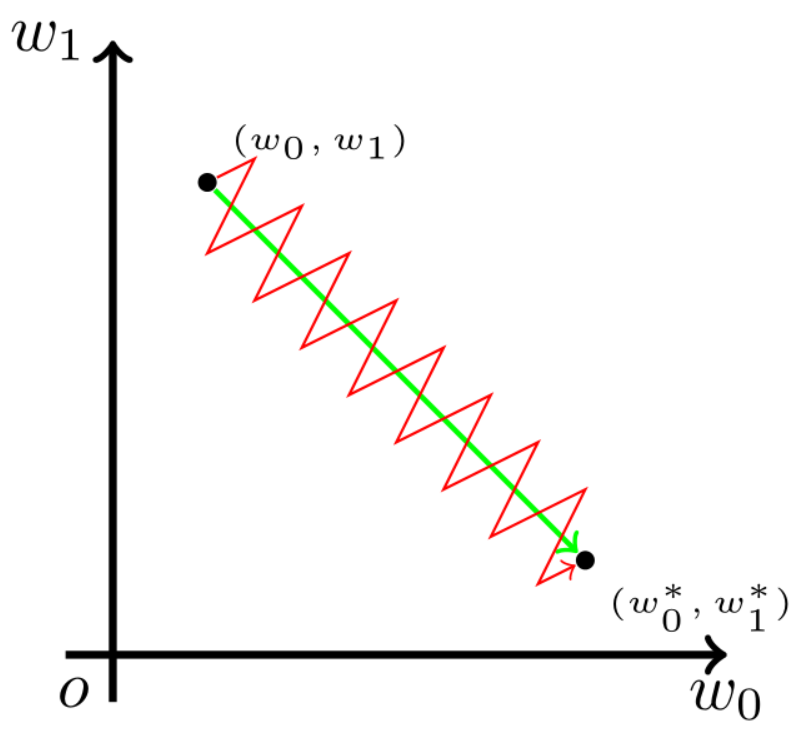
Sigmoid函数的输出值恒大于0，这会导致模型训练的收敛速度变慢。举例来讲，对 $\sigma \left ( \sum_{i}{w}_{i}*{x}_{i}+b \right )$ ，如果所有 ${x}_{i}$ 均为正数或负数，那么其对 ${w}_{i}$ 的导数总是正数或负数，这会导致如下图红色箭头所示的阶梯式更新，这显然并非一个好的优化路径。深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。

幂运算相对耗时

相对于前两项，这其实并不是一个大问题，我们目前是具备相应计算能力的，但面对深度学习中庞大的计算量，最好是能省则省。

参考自：

聊一聊深度学习的activation function - 知乎
谈谈激活函数以零为中心的问题 | 始终
cs231n_激活函数_unit gaussian_zone_chan的博客-CSDN博客
【深度学习】5-从计算图直观认识“激活函数不以零为中心导致收敛变慢”_收敛的很慢_清风莫追的博客-CSDN博客
【深度学习】1-权重参数全相同值初始化，导致无法训练_深度学习所有参数初始化一致有什么问题_清风莫追的博客-CSDN博客文章来源地址https://uudwc.com/A/k9yPv