深度学习常用优化器总结

一、优化器的定义

优化器（optimizer）本质上是一种算法，用于优化深度学习模型的参数，通过不断更新模型的参数来最小化模型损失。在选择优化器时，需要考虑模型的结构、模型的数据量、模型的目标函数等因素。

二、常用优化器

BGD（Batch Gradient Descent）

定义

BGD是梯度下降法最原始的形式，它的基本思想是在更新参数时使用所有样本来进行更新

公式

公式如下，假设样本总数为N，

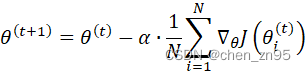
特点

BGD得到的是一个全局最优解，但是每迭代一步，都要用到训练集的所有数据，如果样本数巨大大，那上述公式迭代起来则非常耗时，模型训练速度很慢；迭代次数少

代码示例

# 数据
inputs = ...

# 标签
labels = ...

# 模型
model = ...

# 损失函数
criterion = ...

# 优化器
optimizer = torch.optim.SGD(model.parameters())

# 训练
for i in range(epochs):
    # 计算损失
    outputs = model(inputs)
    loss = criterion(outputs, labels)

    # 计算梯度
    optimizer.zero_grad()
    loss.backward()

    # 更新参数
    optimizer.step()

SGD（Stochastic Gradient Descent）

定义

SGD的基本思想是，更新参数时使用随机选取的一个样本来进行更新

公式

公式如下，

其中， $\theta ^{(t))}$ ：模型在第t次迭代时的参数值， $\alpha$ ：学习率，：损失函数 $J(\theta )$ 关于模型参数 $\theta$ 的梯度。

特点

SGD的优点是实现简单、效率高，缺点是收敛速度慢、容易陷入局部最小值；迭代次数多

代码示例

# 数据
inputs = ...

# 标签
labels = ...

# 模型
model = ...

# 损失函数
criterion = ...

# 优化器
optimizer = torch.optim.SGD(model.parameters())

# 训练
for i in range(epochs):
    for input, label in zip(inputs, labels)
        # 计算损失
        output = model(input)
        loss = criterion(output, label)

        # 计算梯度
        optimizer.zero_grad()
        loss.backward()

        # 更新参数
        optimizer.step()

MBGD（Mini-batch Gradient Descent）

定义

由BGD和SGD可以看出，它们有各的优缺点，那么能不能在这两种方法的性能之间取得一个折中呢？即，算法的训练过程比较快，而且保证最终参数训练的准确率，而这正是MBGD的初衷。MBGD在每次更新参数时使用b个样本

公式

特点

训练过程较稳定；BGD可以找到局部最优解，不一定是全局最优解；若损失函数为凸函数，则BGD所求解一定为全局最优解

代码示例

# 数据
inputs = ...

# 标签
labels = ...

# 模型
model = ...

# 损失函数
criterion = ...

# 优化器
optimizer = torch.optim.SGD(model.parameters())

# mini batch大小
b = ...

# 训练
optimizer.zero_grad()
for epoch in range(epochs):
    for i, (input, label) in enumerate(zip(inputs, labels))
        ni = i + len(inputs) * epoch        

        # 计算损失
        output = model(input)
        loss = criterion(output, label)

        # 计算梯度
        loss.backward()
        
        if ni % b == 0:
            # 更新参数
            optimizer.step()
            optimizer.zero_grad()

Adam（Adaptive Moment Estimation）

定义

Adam是一种近似于随机梯度下降的优化器，它的基本思想是，通过计算模型参数的梯度以及梯度平方的加权平均值（一阶动量和二阶动量），来调整模型的参数

公式

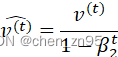
其中，

$g^{(t)}$ ：模型参数在第t次迭代时的梯度，

$m^{(t)}$ 和 $v^{(t)}$ ：模型参数在第t次迭代时的一阶动量和二阶动量，

$\beta _{1}$ 和 $\beta _{2}$ ：超参数（默认是0.9和0.999），

$\beta _{1}^{t}$ 和 $\beta _{2}^{t}$ ： $\beta _{1}$ 和 $\beta _{2}$ 的t次方，

和：偏差纠正后的一阶和二阶动量（由于m和v的初始值为0，在训练初期可能导致一阶动量和二阶动量偏向于0，因此需要对它们进行偏差修正；在训练初期，修正后的m、v会变大，在训练后期，修正前后的m、v差别不大），

"""
一阶动量及二阶动量初始化
"""

# Exponential moving average of gradient values
state['exp_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)

# Exponential moving average of squared gradient values
state['exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)

$\alpha$ ：学习率，

$\varepsilon$ ：值为非常小的常数（默认是1e-8，防除0）

特点

Adam计算效率高，收敛速度快；需要调整超参数；能够自适应地调整每个参数的学习率，从而提高模型的收敛速度和泛化能力；

代码示例

# 数据
inputs = ...

# 标签
labels = ...

# 模型
model = ...

# 定义优化器
optimizer = torch.optim.Adam(model.parameters(), lr=0.1, betas=(0.9, 0.999))

# 损失函数
criterion = ...

# 训练模型
for i in range(epochs):
    # 前向传播
    outputs = model(inputs)
    # 计算损失
    loss = criterion(outputs, labels)

    # 计算梯度
    optimizer.zero_grad()
    loss.backward()

    # 更新参数
    optimizer.step()

三、总结

SGD

SGD只使用当前的梯度方向进行更新，容易受到数据噪声的影响，训练不稳定，因此可能会需要更小的学习率，才能达到良好的收敛性能
SGD最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点
SGD的实现相对简单，具有较低的计算开销，并且在一些数据集和模型中可能比Adam更有效

Adam

Adam在梯度下降过程中考虑历史梯度及梯度平方的平均值，能够更快地收敛，但Adam比SGD更容易过拟合，因为它考虑了历史梯度的平均值，可能导致过于自信地更新参数
Adam适用于处理大规模数据和参数的情况
Adam的学习率不是单调变化的，可能在训练后期引起学习率的震荡，导致模型无法收敛，但可以通过以下公式进行约束，使学习率单调递减

【参考文章】

Adam优化器（通俗理解）_Longer2048的博客-CSDN博客

http://bbs.xfyun.cn/thread/46940&wd=&eqid=f85ffc5f000f860300000006642b26be文章来源地址https://uudwc.com/A/monWW