异方差无法用OLS进行估计的根源问题:方差较大的数据包含的信息量较小,但OLS是对所有数据进行相同的处理。异方差的问题并不会影响估计量的无偏性、一致性、渐近正态性,只是效率较低使得t检验和F检验失效。
说白了就是回归出来的系数不会改变,只是可能会导致显著性的结果不准确。
而选用GLS以及WLS进行回归可以对不同特征的数据进行不同的处理以提高估计效率。
理论知识
- 异方差的检验
残差图、怀特检验、BP检验
- 异方差的处理
- OLS+标准误(robust)的方式
- 广义最小二乘法(GLS)(相比于上一种方法更为有效):广义最小而成的中心思想就是将模型进行变量转换,进而使得扰动项满足假定。
- 加权最小二乘法(WLS):是GLS的特例
- 可行广义最小二乘法(FGLS):GLS和WLS的问题在于,在运算中是已知总体的扰动项的协方差矩阵的,但事实上这很难实现,故FGLS则可以根据样本数据估计协方差矩阵。
- 如何选择处理方法
在实际运用中,主要是在OLS+标准误与FGLS之间选择,FGLS的最大前提就是对协方差矩阵的一致估计是准确的,但是如果并不准确,则从一开始就是错误的,进而导致不正确的统计推断。而OLS+标准误的方法对回归系数以及标准误的估计都是一致的,对协方差的估计是否准确并无要求。故在一般情况下,仍然选择更为稳健的OLS+标准误方法,而不是FGLS,但在协方差矩阵估计正确的条件下,显然是FGLS更为有效。
Stata操作
- 异方差的检验(均需要先进行回归)
1、残差图
观察时看是否出现残差值是否在一个数值附近,如下图能够明显看出残差在纵轴上的数值波动较大
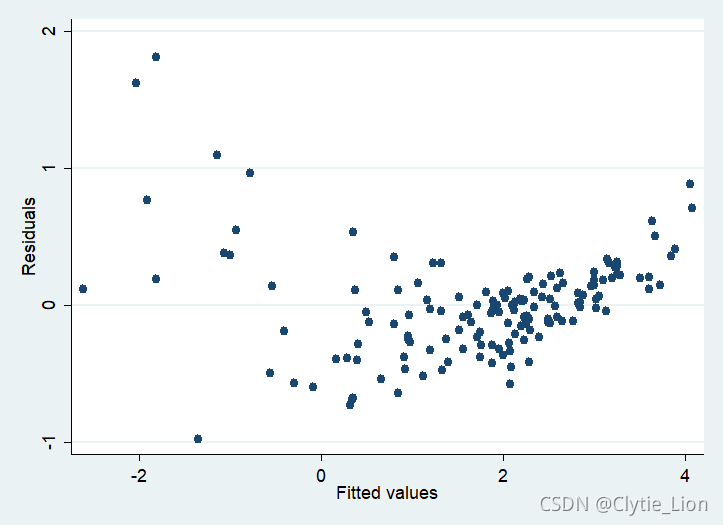
///残差与拟合值
rvfplot
///残差与某个变量
rvpplot varname
2、怀特检验
看表格上面的Prob>chi2的p值为0.000,故拒绝同方差的假设,即存在异方差问题。
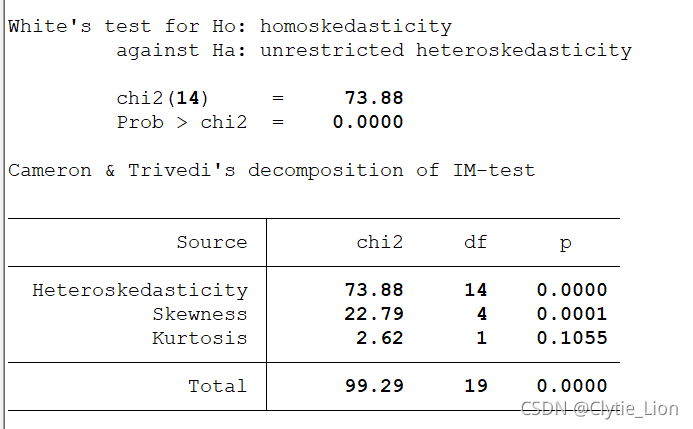
estat imtest,white
3、BP检验
观察p值如果小于0.01,则表示强烈拒绝原假设,即方差不同

///使用拟合值y进行检验
estat hettest
///使用所有解释变量
estat hettest,rhs
///使用个别指定解释变量
estat hettest [varlist]
///前面的BP检验自身是以扰动项服从正态分布为假定前提的,后可放宽至独立同分布(iid)
///(该方法较为常用)
estat hettest,iid
estat hettest,rhs iid
estat hettest [varlist],iid
- WLS(需要经过一系列的计算得到方差的估计值)
可直接保留至do文件
///qui 表示不显示结果,因为我们并不需要这个回归结果
qui reg y x
///计算残差,res是residual的简称,即预测残差
predict e1,res
///因为残差是标准差,需要进行平方得到方差
g e2=e1^2
///取对数进行辅助回归,noc表示不显示常数项
///在此次回归中,可以通过R方的大小判断x解释方差变动的比例,进而进一步判断是否存在方差随着解释变量变动而变动的现象
g lne2=log(e2)
reg lne2 x,noc
///计算回归后拟合出来的方差项,此处predict 默认得到拟合值,并后面接的新变量名默认为你拟合值的变量名
predict lne2f
///去除对数化
g e2f=exp(lne2f)
///最终进行WLS回归文章来源:https://uudwc.com/A/nMZW
reg y x [aw=1/e2f]文章来源地址https://uudwc.com/A/nMZW
