现实生活中，很多数据呈现季节性特征。一个最简单的案例就是羽绒服在“冬季”销售量明显高于“夏季”。所以羽绒服售卖月份与售卖数量的模型就呈现季节性。
在对于季节性的研究中，最终目的为能够进行准确的预估。本文将阐述相关方法，相关判定准确性条件等。
季节性模型
首先，可以直观的观察一下季节性模型数据呈现的波动曲线：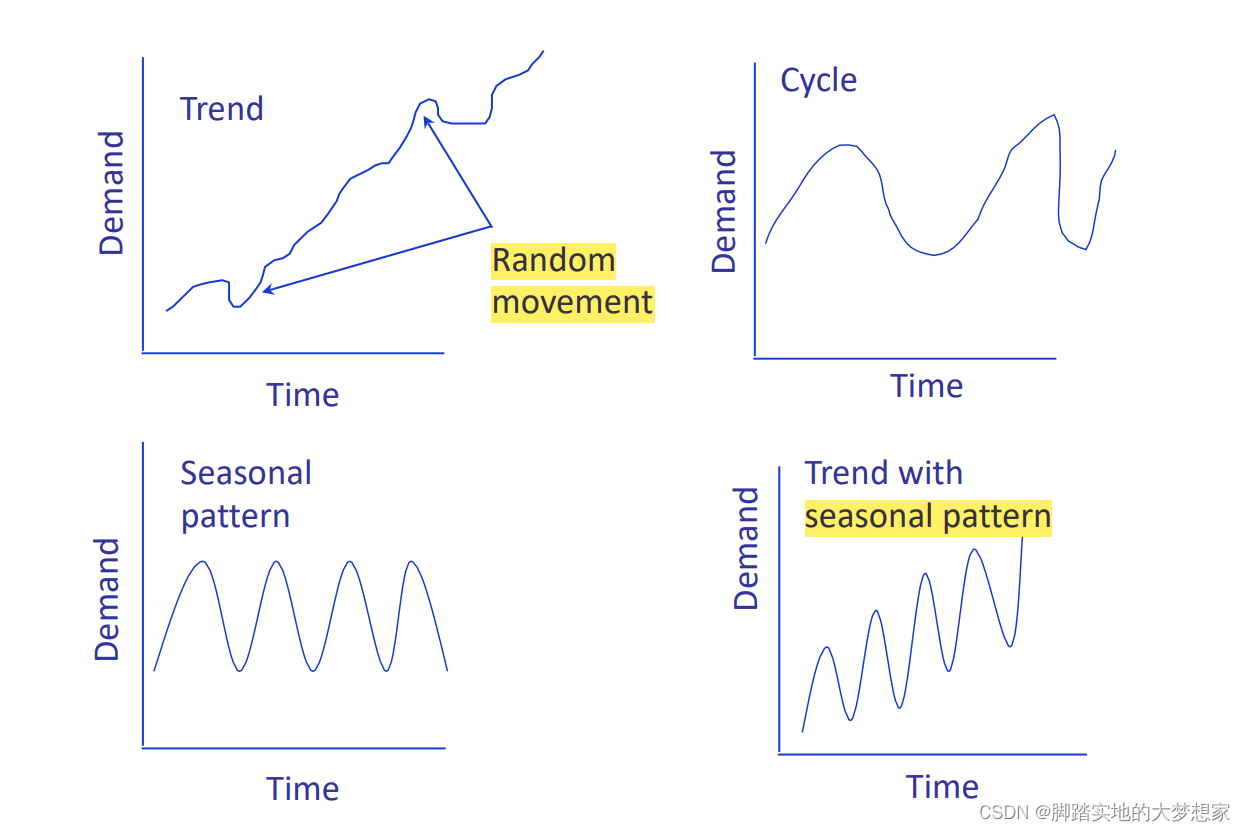
上图中，图1呈现的是具有趋势的模型数据；图2呈现的是具有循环趋势的数据；图3呈现的是季节性数据曲线；而图4呈现的是同时具有季节性以及趋势的波动曲线。
五种判定预测的方案
通过判定方案，判断我们的预测是否合理，预测模型是否可行。
误差 Bias
B
i
a
s
=
∑
(
A
c
t
u
a
l
−
F
o
r
e
c
a
s
t
)
n
=
∑
E
r
r
o
r
n
Bias = \frac {\sum {(Actual-Forecast)}} n = \frac {\sum {Error}} n
Bias=n∑(Actual−Forecast)=n∑Error
上式中，
A
c
t
u
a
l
Actual
Actual 代表实际值，
F
o
r
e
c
a
s
t
Forecast
Forecast 代表预测值，
E
r
r
o
r
Error
Error 代表误差，即实际值与预测值的差值。
需要注意的是，
B
i
a
s
Bias
Bias 的结果可能为负值。
绝对误差 MAD - Mean Absolute Deviation
绝对误差的平均值。与 B i a s Bias Bias 唯一不同在于不存在负值。
M A D = ∑ ∣ A c t u a l − F o r e c a s t ∣ n = ∑ ∣ E r r o r ∣ n MAD = \frac {\sum {|Actual-Forecast|}} n = \frac {\sum {|Error|}} n MAD=n∑∣Actual−Forecast∣=n∑∣Error∣
均方误差 MSE - Mean Square Error
误差平方的平均值。均方误差与方差的区别在于：
均方误差计算的是各个数据偏离真实值的平方和；
而方差则是计算各个数据与平均值的之差的平方和。
M S E = ∑ ( A c t u a l − F o r e c a s t ) 2 n = ∑ E r r o r 2 n MSE = \frac {\sum {(Actual-Forecast)^2}} n = \frac {\sum {Error^2}} n MSE=n∑(Actual−Forecast)2=n∑Error2
标准差 Standard Error
标准差为方差的平方根，在本模型中，可为均方误差的平方根，即：
S t a n d E r r o r = M S E StandError = \sqrt {MSE} StandError=MSE
平均误差百分比 MAPE - Mean Absolute Percentage Error
平均误差百分比，拆开来理解，首先计算的是绝对误差占真实值的比例，该比例的和的平均值即为MAPE。
M A P E = ∑ ∣ A c t u a l − F o r e c a s t ∣ A c t u a l n ∗ MAPE = \frac {\sum {\frac {|Actual-Forecast|} {Actual}} } n* MAPE=n∑Actual∣Actual−Forecast∣∗ 100%
五种预测方案
Naïve 朴素法
“昨天多少今天我就预测是多少”。
e
.
g
.
e.g.
e.g.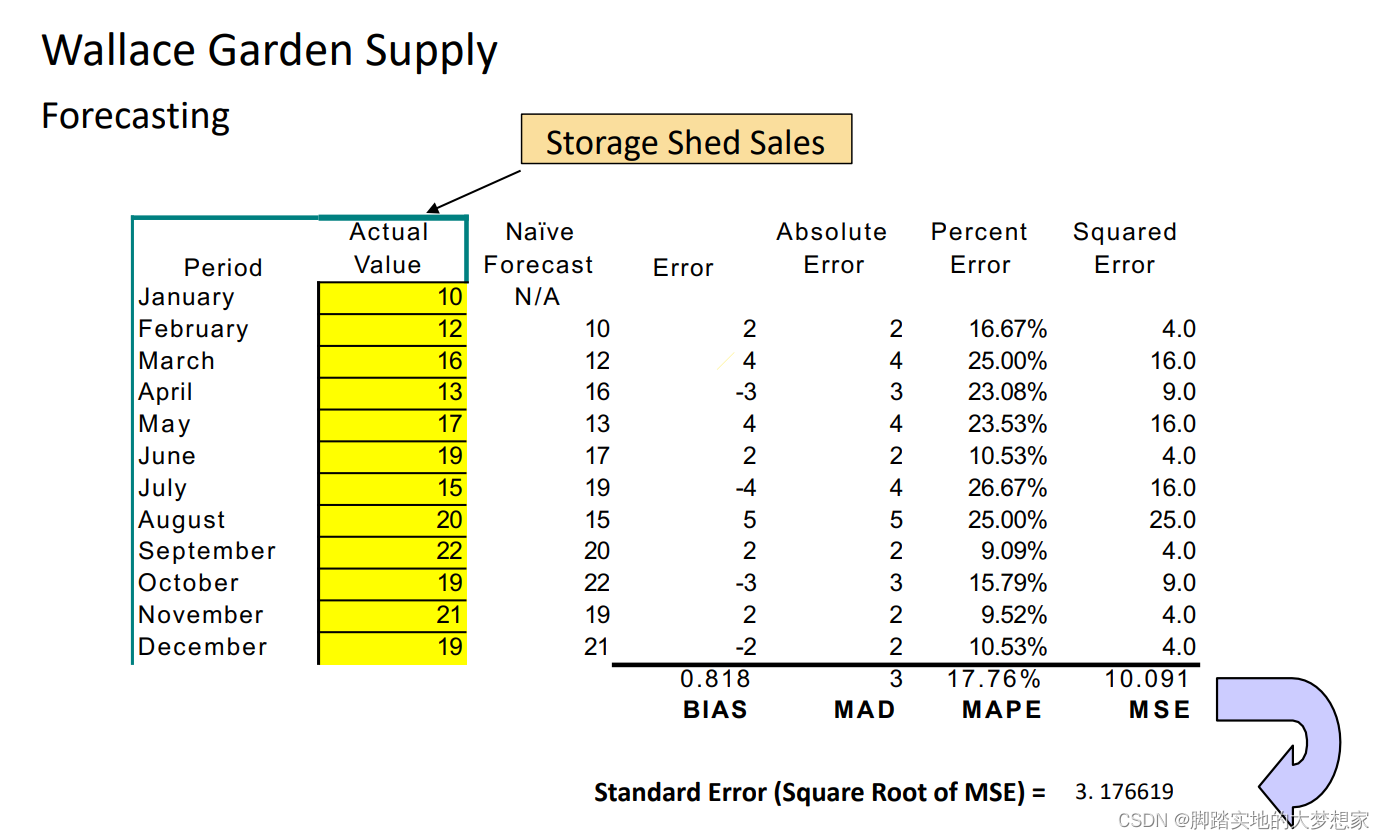
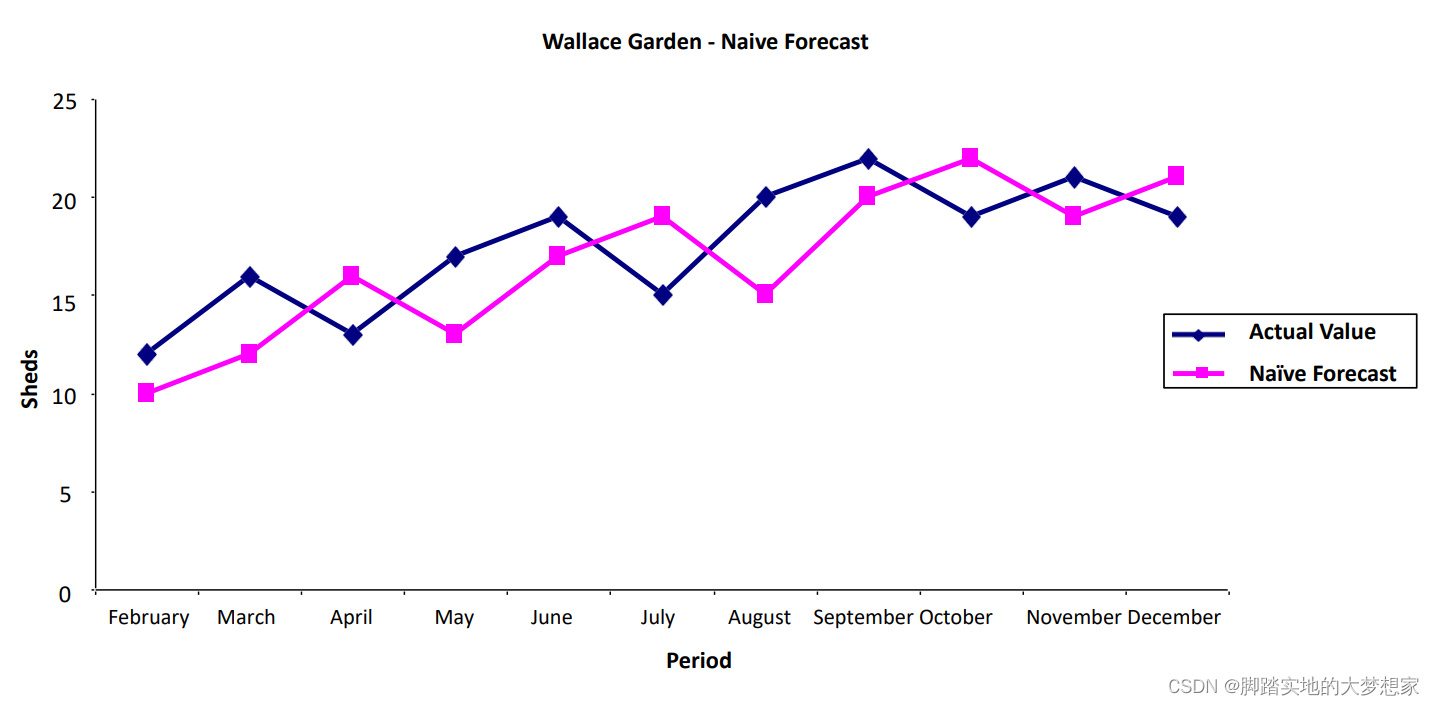
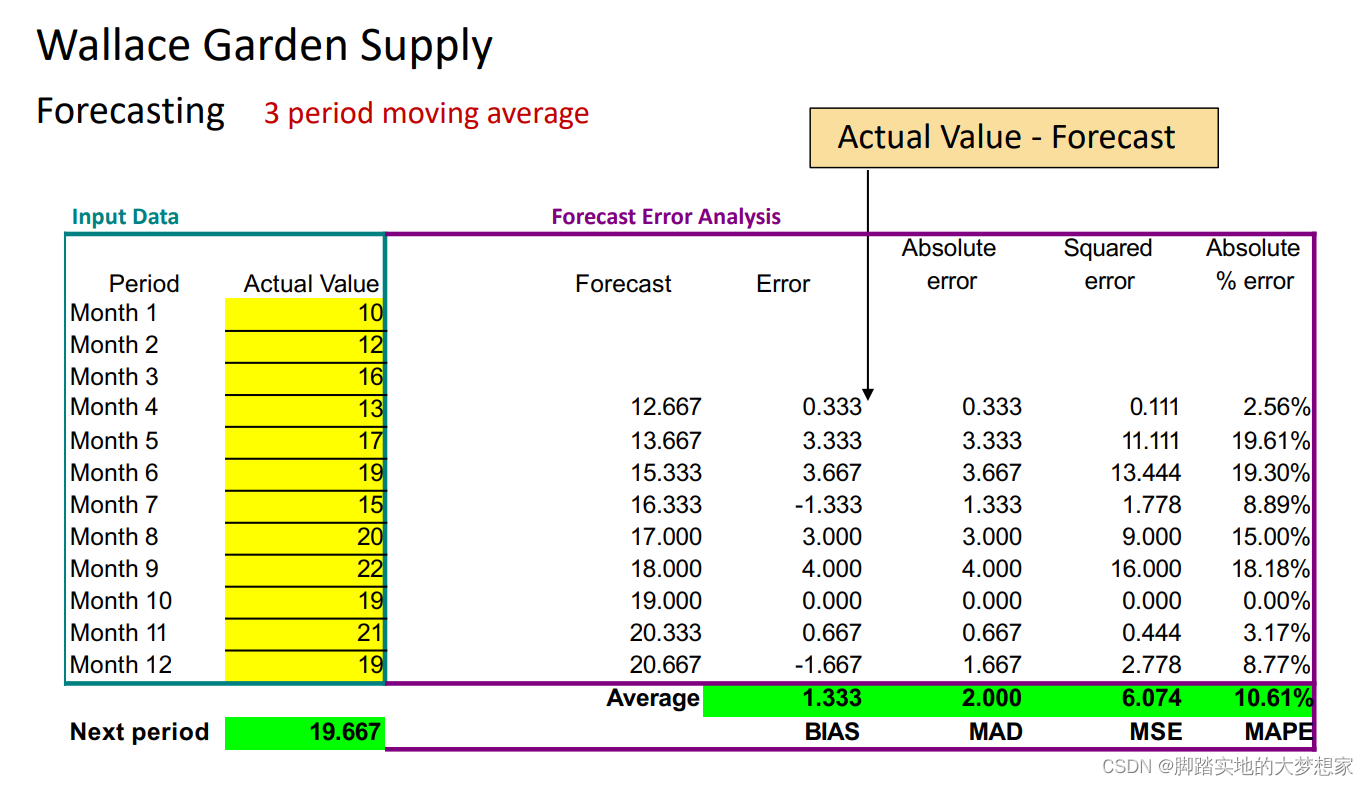
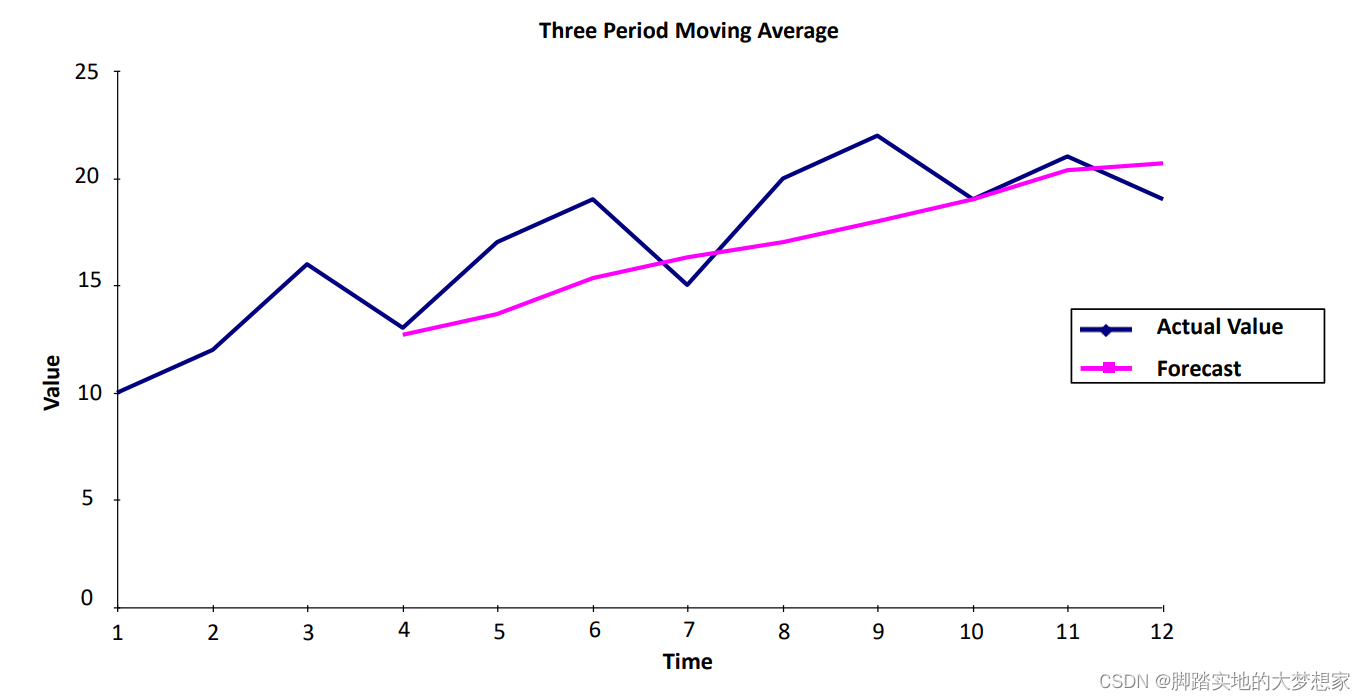
n-period Moving Average 平均值法
假设 n = 3 n=3 n=3，“我根据前三天的结果预估今天的结果”。
e
.
g
.
e.g.
e.g.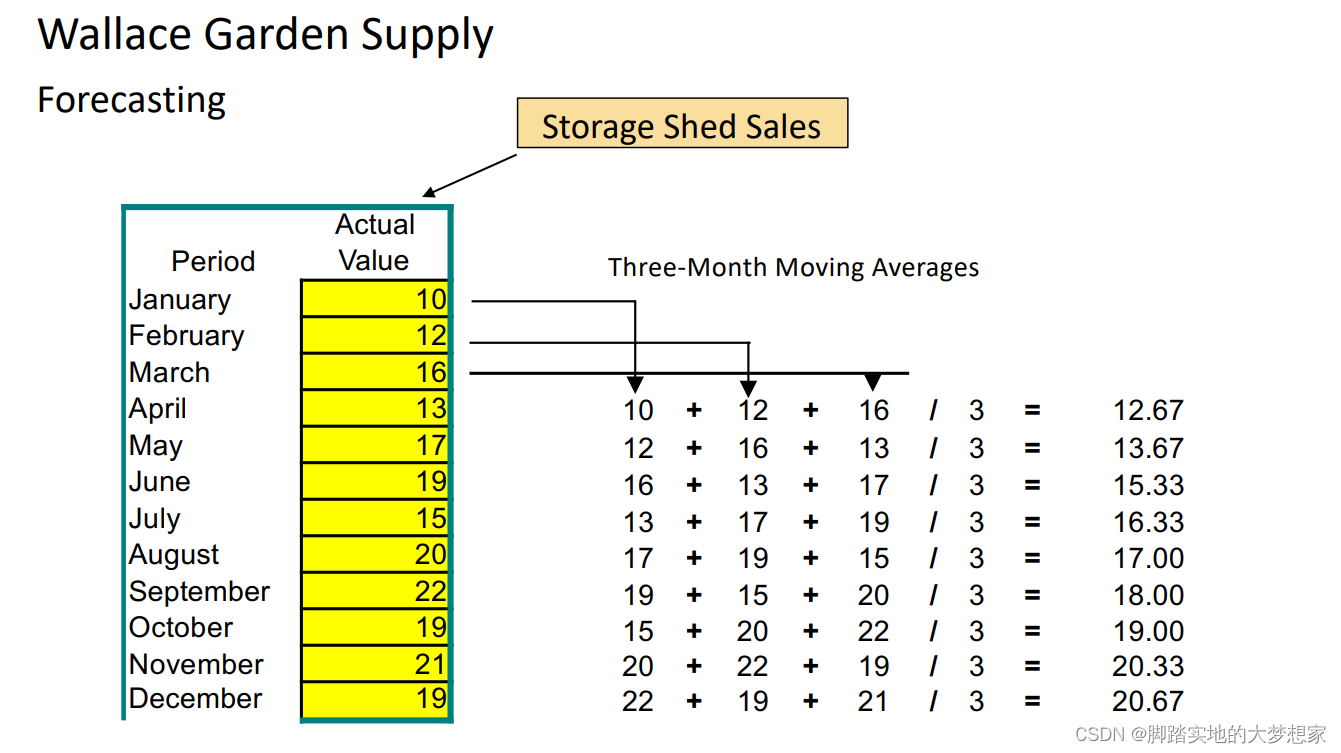
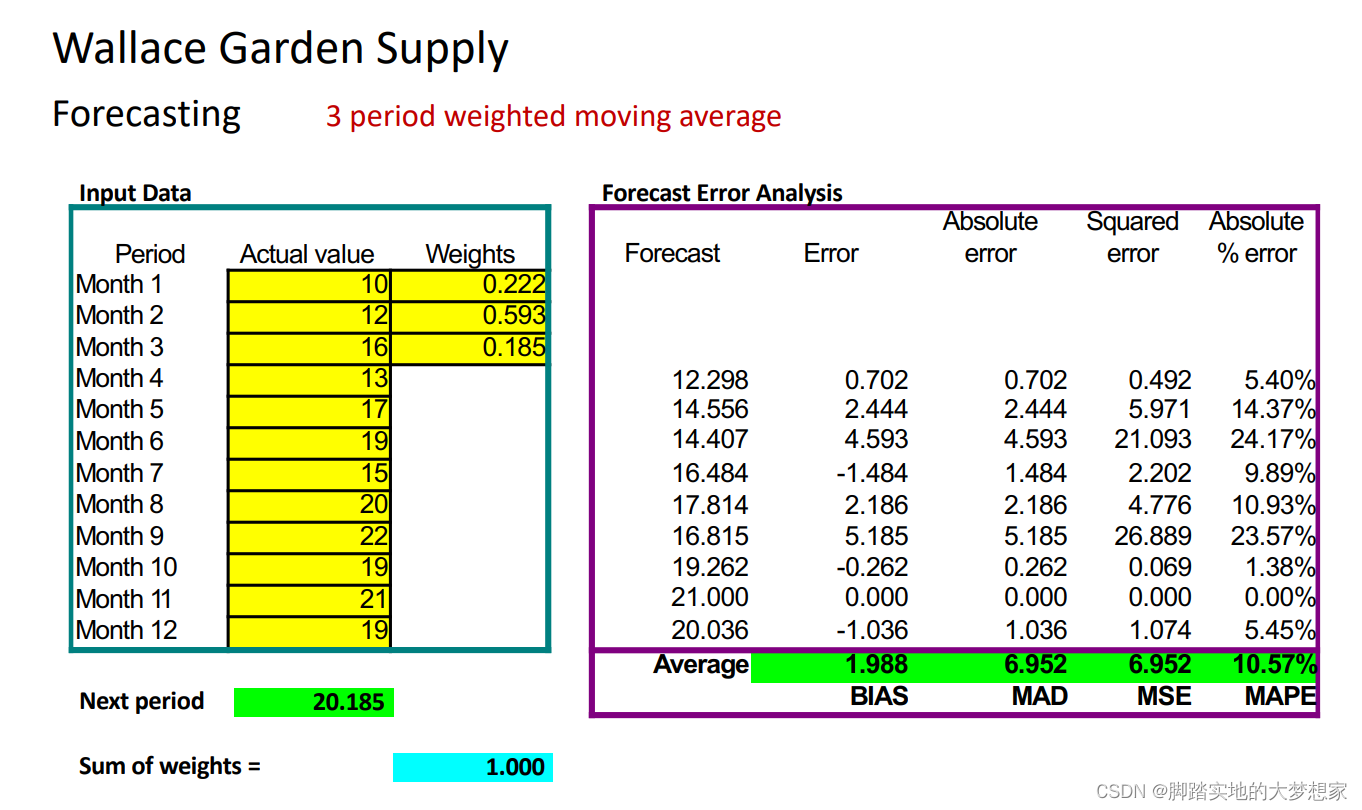
n-period Weight Moving Average 权重平均值法
假设n=3，而且“我觉得第二天的结果比第一天重要，第一天结果比第三天重要！”
e
.
g
.
e.g.
e.g. 假设
w
2
=
0.593
,
w
1
=
0.222
,
w
3
=
0.185
w_2=0.593,w_1=0.222,w_3=0.185
w2=0.593,w1=0.222,w3=0.185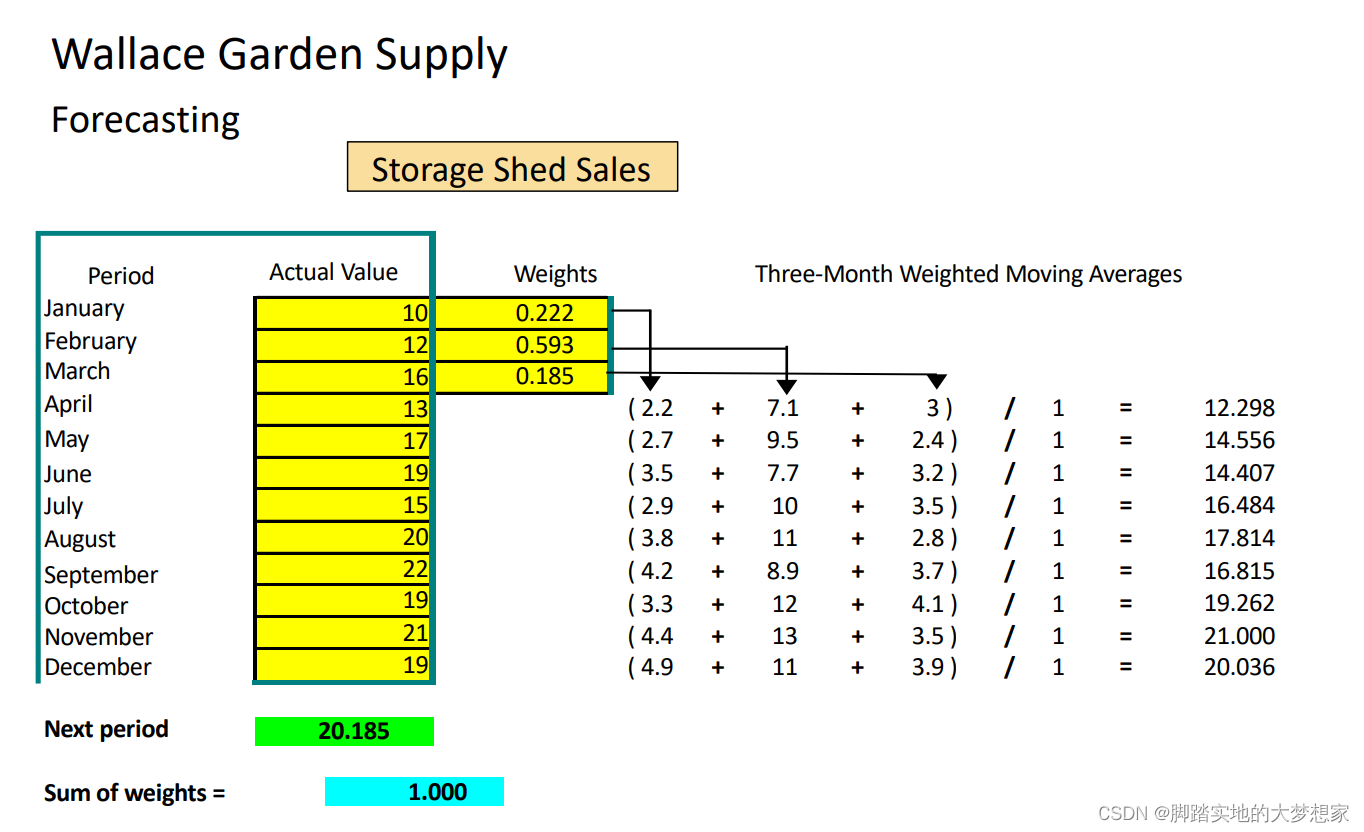
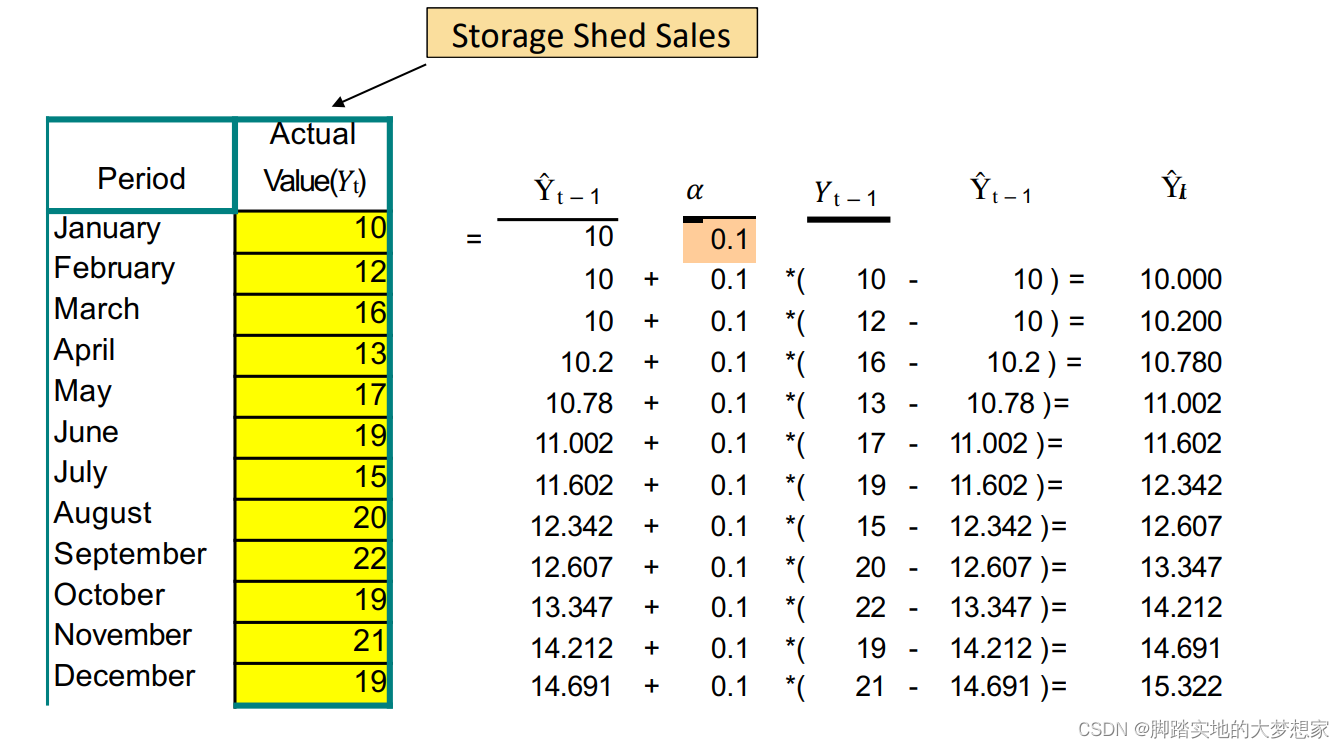
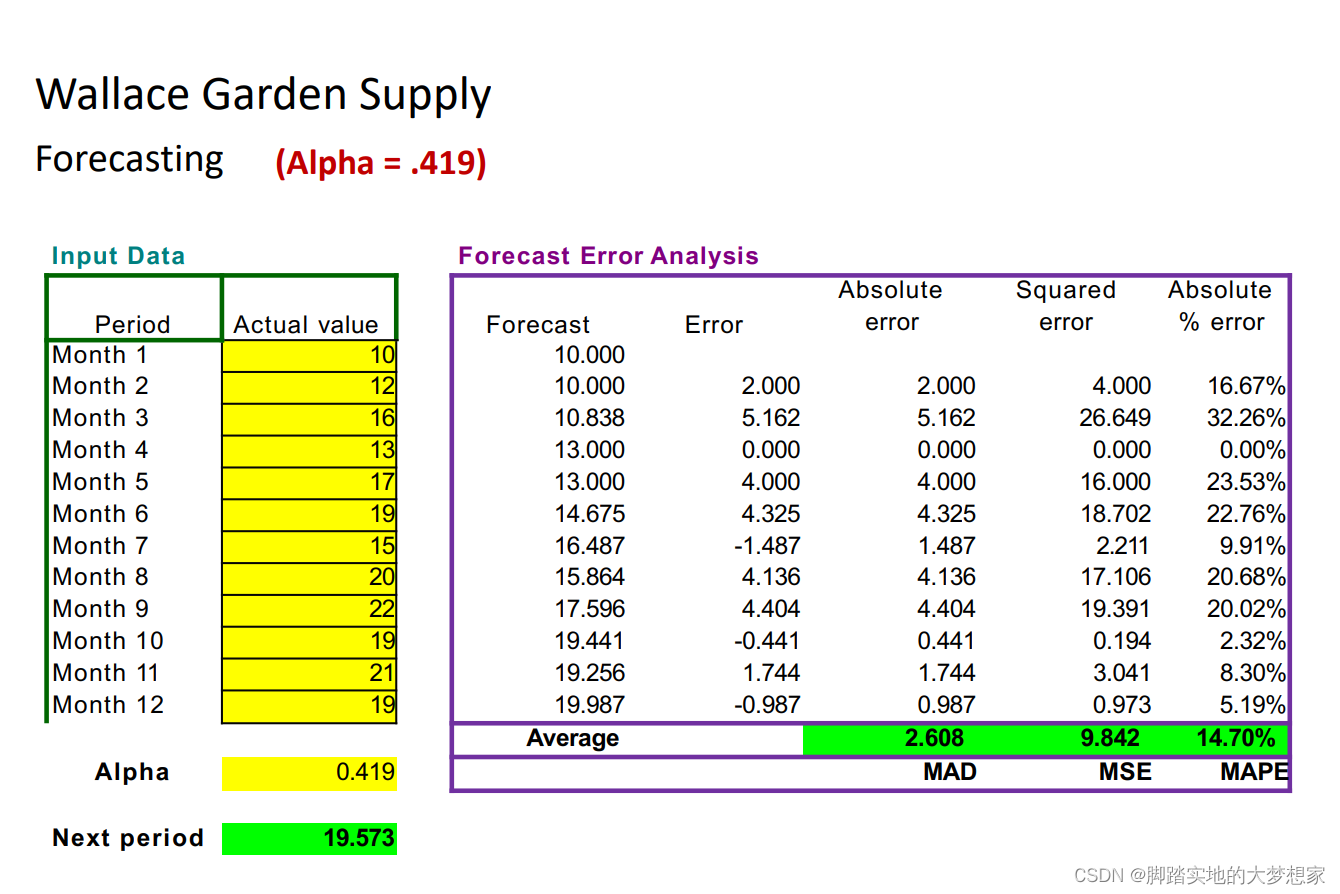
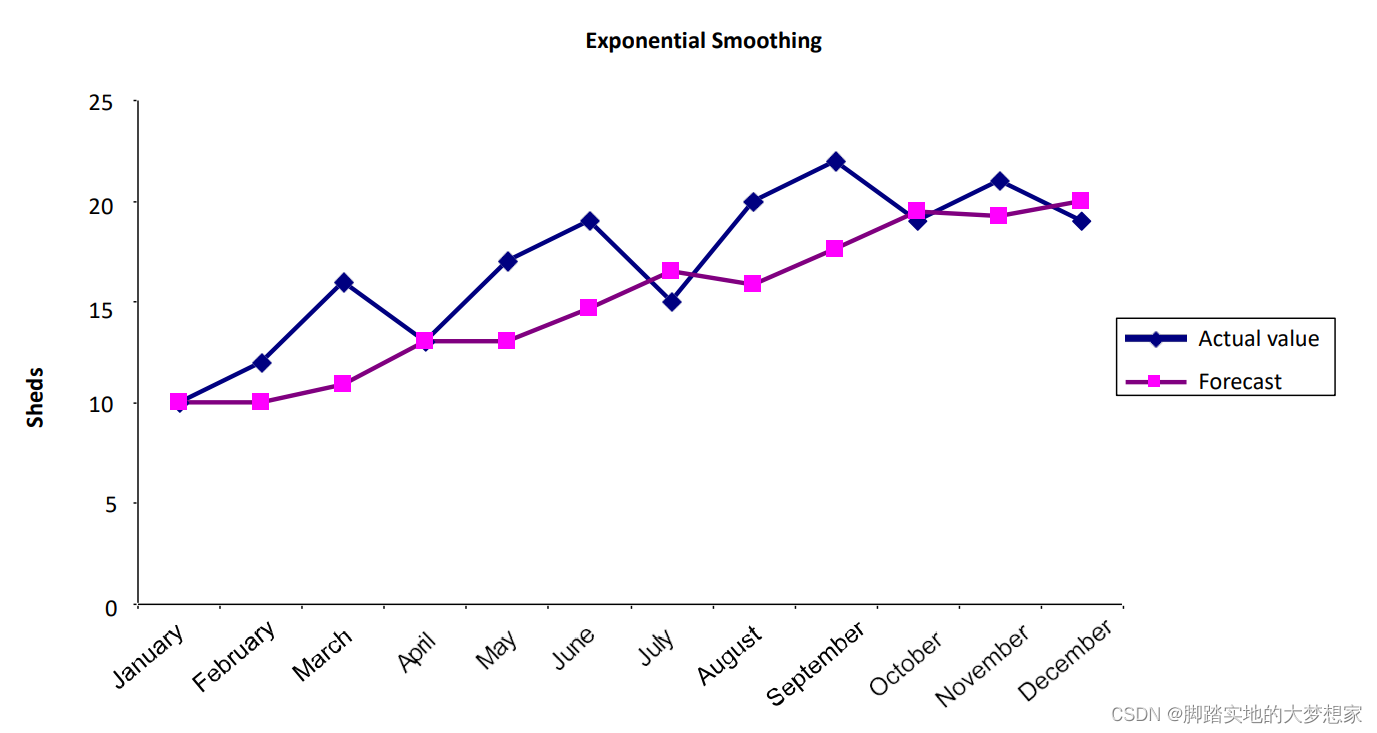
Simple Exponential smoothing 平滑法
“今天的预估与昨天的实际值以及昨天的预估有关！”
F
o
r
c
a
s
t
(
i
)
=
α
∗
A
c
t
u
a
l
(
i
−
1
)
+
(
1
−
α
)
∗
F
o
r
c
a
s
t
(
i
−
1
)
Forcast(i) = α*Actual(i-1)+(1-α)*Forcast(i-1)
Forcast(i)=α∗Actual(i−1)+(1−α)∗Forcast(i−1)
F
o
r
c
a
s
t
(
i
)
=
F
o
r
c
a
s
t
(
i
−
1
)
+
α
∗
(
A
c
t
u
a
l
(
i
−
1
)
−
F
o
r
c
a
s
t
(
i
−
1
)
)
Forcast(i) =Forcast(i-1)+α*(Actual(i-1)-Forcast(i-1))
Forcast(i)=Forcast(i−1)+α∗(Actual(i−1)−Forcast(i−1))
第五种预测方案：去季节化
去季节化方案，Deaseasonalized，该方案与前几种不同的在于，他试图找到数据之间的规律与趋势，通过趋势与重新季节化得到一个合理的预测结果。
所以我们使用 “去季节化” 这种方案的准确步骤为：去季节化->预测->季节化
D e a s e a s o n a l i z e d D a t a = A c t u a l V a l u e S e a s o n a l I n d e x Deaseasonalized~Data=\frac {Actual~Value} {Seasonal~Index} Deaseasonalized Data=Seasonal IndexActual Value
R e s e a s o n a l i z e d F o r e c a s t = ( D e s e a s o n a l i z e d F o r e c a s t ) ∗ ( S e a s o n a l I n d e x ) Reseasonalized~Forecast=(Deseasonalized~Forecast)*(Seasonal~Index) Reseasonalized Forecast=(Deseasonalized Forecast)∗(Seasonal Index)
所以我们如果想要通过该方法预测数据，则我们需要得到
S
e
a
s
o
n
a
l
I
n
d
e
x
Seasonal~Index
Seasonal Index，即季节化模型。
下面我们通过一个案例来得到 Seasonal~Index 以及去季节化
e . g . e.g. e.g. 假设存在季节化数据如下：
该表含义为2019年上半年，有113个订单，下半年有236个订单…可以很明显的发现上半年的订单明显低于下半年的订单，而且2019年到2020年到2021年存在某种趋势。
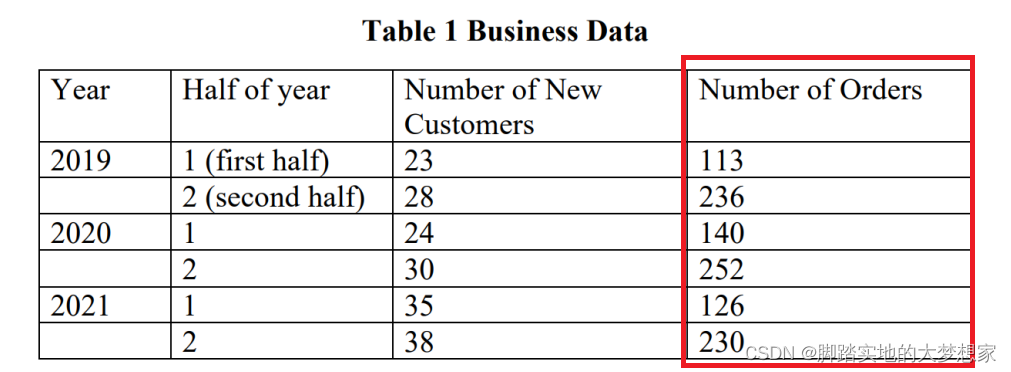
计算得到每年销售订单的平均值：
得到Seasonalize Index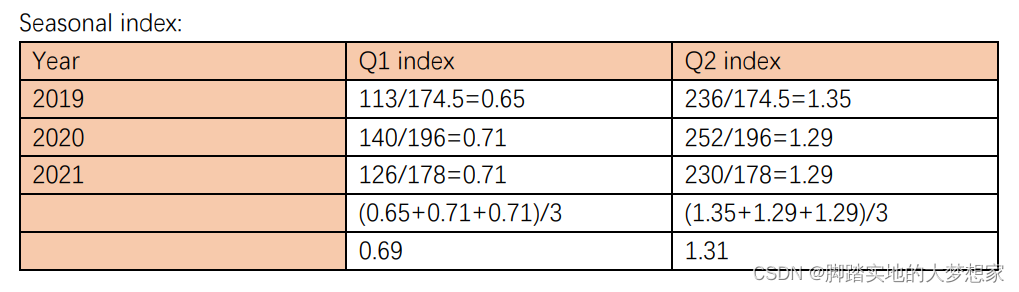
进行去季节化
通过python绘图，我们发现我们成功的将季节化的影响去除，从而清晰的看出订单在2019、2020到2021年的波动曲线（蓝色部分）：红色部分为去季节化前的波动曲线。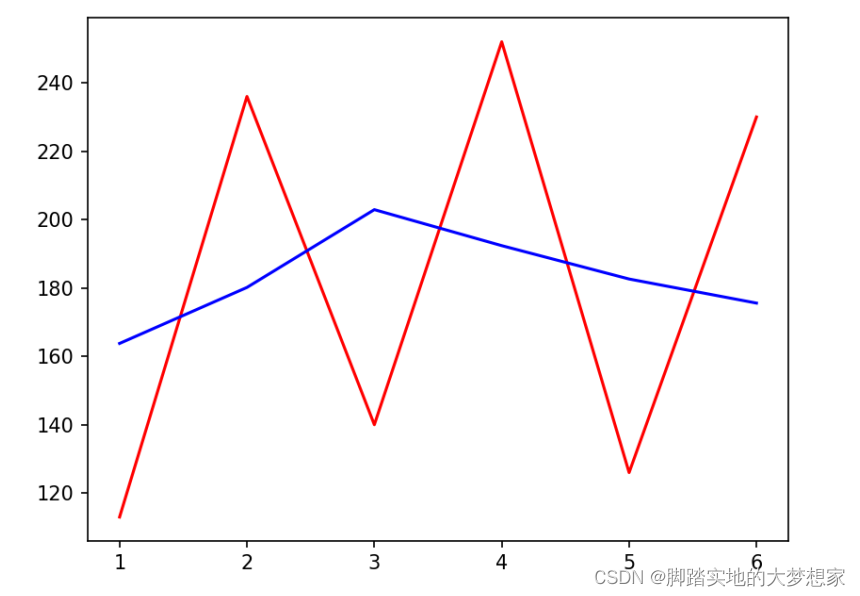
文章来源：https://uudwc.com/A/nndX
参考资料：
[1] 百度百科. 偏差
[2] 百度知道. 均方误差与方差
[3] 华莱士花园预估数据. 2022. 理工大学. 大数据课程
[4] 销售订单案例. 2022. 包玉刚图书馆. 大数据模型文章来源地址https://uudwc.com/A/nndX
