上期我们已经学习了数据结构中的栈,这期我们开始学习队列。
目录
1.队列的概念及结构
2.队列的实现
队列结构体定义
常用接口函数
初始化队列
队尾入队列
队头出队列
获取队列头部元素、
获取队列队尾元素
获取队列中有效元素个数
检测队列是否为空
销毁队列
3.循环队列
1.队列的概念及结构
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头

从网上找来的队列结构示意图:

2.队列的实现
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。
队列结构体定义
我们使用的是不带头节点的单向链表来实现队列,而队列要在队尾插入数据,因此每次都要遍历链表找队尾,这样会使得程序的运行效率变低。这里采取了一种解决办法:定义一个指向队尾的指针tail, 每次插入新的数据就只要将tail中的next指针指向新节点即可,同时插入新的数据后再更新tail的位置。
typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next;
QDataType data;
}QNode;这里单独定义了一个结构体来存储头指针head和尾指针tail。
typedef struct Queue
{
QNode* head;
QNode* tail;
}Queue;常用接口函数
//初始化
void QueueInit(Queue* pq);
//插入数据
void QueuePush(Queue* pq, QDataType x);
//销毁
void QueueDestroy(Queue* pq);
//弹出
void QueuePop(Queue* pq);
//取队头数据
QDataType QueueFront(Queue* pq);
//取队尾数据
QDataType QueueBack(Queue* pq);
//判断是否为空
bool QueueEmpty(Queue* pq);
//计算大小
int QueueSize(Queue* pq);初始化队列
由于这里使用的是不带头节点的单向链表,所以初始化队列只需要将头指针和尾指针都指向空即可。如果是要定义一个带头节点的链表,则需要在这里创建一个头节点
//初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
}队尾入队列
由于我们已经将链表的尾部给记录了下来,所以不需要遍历链表,只要尾部节点中的next指针指向新节点

同时需要判断链表是否为空,如果链表是第一次插入数据,需要将头指针和尾指针都指向新节点。
![]()
//队尾插入数据
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
//创建新节点
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
printf("malloc fail\n");
exit(-1);
}
newNode->data = x;
newNode->next = NULL;
//将新节点链接起来
if (pq->tail == NULL)
{
pq->head = pq->tail = newNode;
}
else
{
pq->tail->next = newNode;
pq->tail = newNode;
}
}队头出队列
在弹出数据之前,要判断链表是否为空,这里可以用assert断言:
接下来是具体的弹出操作:
- 判断队列是否只有一个节点。如果是,表示队列中只剩下一个节点,直接释放这个节点,同时将头指针和尾指针都置为空。
- 如果队列中有多个节点,将头指针
pq->head指向下一个节点,然后释放原来的头节点。这样就完成了一个节点的弹出操作。
//弹出
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
}获取队列头部元素、
返回队列头节点的数据 pq->head->data 即可。
//取队头数据
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}获取队列队尾元素
- 返回队列尾节点的数据
pq->tail->data即可。
//取队尾数据
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}获取队列中有效元素个数
计算大小有多种方法,常用的两种是:
一种是在定义Queue结构体时增加一个用于计数的变量,每次插入数据就自加一下,弹出数据就自减一下。
typedef struct Queue
{
int size;
QNode* head;
QNode* tail;
}Queue;另外一种是遍历链表,这种方法效率比较低,当然,如果你不在乎这点效率问题,你可以使用这种方法,我们这里也是使用这种方式:
//计算大小
int QueueSize(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
int size = 0;
while (cur)
{
++size;
cur = cur->next;
}
return size;
}检测队列是否为空
如果头节点head为空,则队列为空。
//判断是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL;
} 销毁队列
销毁队列和销毁普通链表一样:
- 使用一个指针
cur指向队列的头节点pq->head。 - 在一个循环中,遍历队列的所有节点,直到
cur为空。 - 循环结束后,将队列的头指针和尾指针都置为空,表示队列已经被销毁。
//销毁
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
3.循环队列
循环队列的概念
实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型 时可以就会使用循环队列。环形队列可以使用数组实现,也可以使用循环链表实现。
循环队列是一种在固定大小的数组或链表上实现的队列,它可以通过循环利用数组或链表中的空间来实现入队和出队操作。当队列满时,新的元素会从开头重新进入队列,实现循环利用。

通常循环队列有两个指针,一个是头指针head,另一个是尾指针tail, 当head和tail指向同一个节点时,表示队列为空。
当从队尾插入一个数据时,tail就会向后移动。当弹出队头数据时,head向后移动。
空的循环队列:
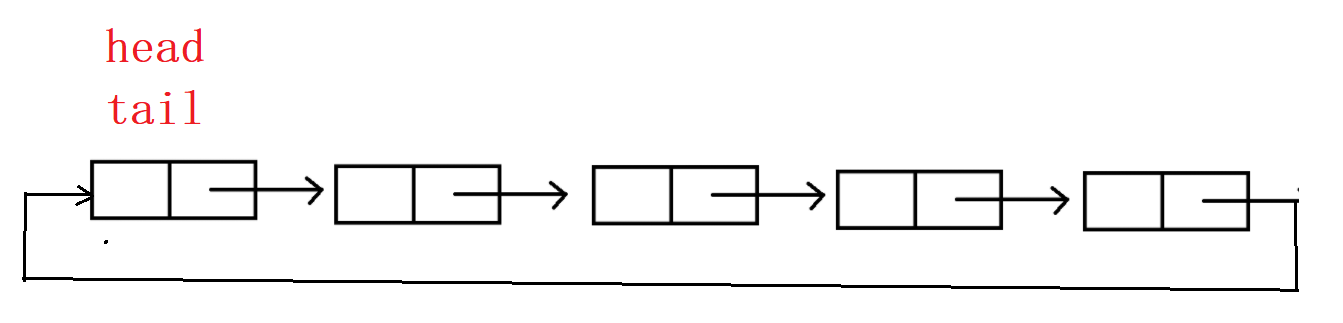
插入3个数据:

弹出一个队首的数据:

按照上面这种情况,当队列已经满了的时候,head和tail也会指向同一个节点。这样我们就无法区分队列是空还是满了。因此想出了这两种方法:
方案一:设置一个变量size计算队列元素个数,如果size与队列容量相等时,说明队列已满。
方案二:多开一个空间,不存储数据。 当 tail->next==head 时,表示已经满了。
一般方案二的实用性较强。

用方案二这种方法我们会发现,如果使用链表的形式实现队列,由于tail每次都是指向尾节点的下一个节点,当我们要取尾节点的数据时,不是很方便。
因此,我们可以使用数组来实现队列。
用数组实现循环队列
原题链接:力扣
 文章来源:https://uudwc.com/A/orM3z
文章来源:https://uudwc.com/A/orM3z
文章来源地址https://uudwc.com/A/orM3z
typedef struct
{
int* a;
int k;
int head;
int tail;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k)
{
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
//带有一个不存储数据的头
obj->a = (int*)malloc(sizeof(int)*(k+1));
obj->k = k;
obj->head = obj->tail = 0;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj)
{
return obj->head == obj->tail;
}
bool myCircularQueueIsFull(MyCircularQueue* obj)
{
int next = obj->tail + 1;
if(obj->tail == obj->k)
{
next = 0;
}
return next == obj->head;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value)
{
if(myCircularQueueIsFull(obj))
{
return false;
}
obj->a[obj->tail] = value;
obj->tail++;
//tail到达数组临界,调整tail位置到开头,以达到循环队列效果
if(obj->tail == obj->k + 1)
{
obj->tail = 0;
}
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj)
{
if(myCircularQueueIsEmpty(obj))
{
return false;
}
obj->head++;
if(obj->head == obj->k + 1)
{
obj->head = 0;
}
return true;
}
int myCircularQueueFront(MyCircularQueue* obj)
{
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
return obj->a[obj->head];
}
int myCircularQueueRear(MyCircularQueue* obj)
{
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
int prev = obj->tail - 1;
if(obj->tail == 0)
{
prev = obj->k;
}
return obj->a[prev];
}
void myCircularQueueFree(MyCircularQueue* obj)
{
free(obj->a);
free(obj);
}