目录
一、栈
1、栈的基本介绍
2、栈的底层实现
二、中缀表达式转后缀表达式
1、拆解中缀表达式
2、中缀转后缀的算法
3、中缀转后缀代码解析
4、对后缀表达式进行计算
一、栈
1、栈的基本介绍
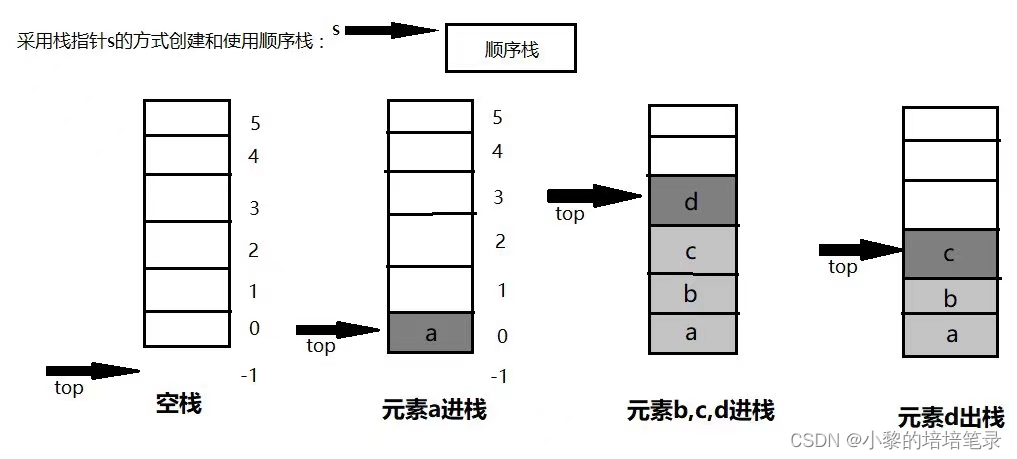
栈是⼀个先⼊后出的有序列表。栈(stack)是限制线性表中元素的插⼊和删除只能在线性表的同⼀端进⾏的⼀种特殊线性表。允许插⼊和删除的⼀端,为变化的⼀端,称为栈顶(Top),另⼀端为固定的⼀端,称为栈底(Bottom)。
根据栈的定义可知,最先放⼊栈中元素在栈底,最后放⼊的元素在栈顶,⽽删除元素刚好相反,最后放⼊的元素最先删除,最先放⼊的元素最后删除。
2、栈的底层实现
▶ (1)创建一个类,模拟栈
maxSize :栈的最大容量
top :表示栈顶
stack :数组用来存储数据
public class Stacks { public int maxSize; public int top ; public int[] stack; //构造器,传入栈的最大容量 public Stacks(int maxSize) { this.maxSize = maxSize; //初始化栈顶的位置为-1,栈空 top = -1; //初始化数组,最大容量为栈的容量 stack = new int[maxSize]; } }▶ (2)判断栈空和栈满
▷ 栈满
//因为底层是数组存储数据,所以索引从0开始, //判断条件为 top == maxSize - 1 public boolean isFull(){ return top == maxSize - 1; }▷ 栈空
public boolean isEmpty(){ return top == -1; }▶ (3)入栈操作
首先判断是否栈满,栈满后则不能继续添加,先对栈顶进行加一,然后再放入数据。
public void push(int data){ //判断是否栈满 if (isFull()){ System.out.println("栈满,无法入栈"); return; } top++; stack[top] = data; }▶ (4)出栈操作
首先判断栈空,出栈操作其实就是将top减一即可,return stack[top--]; 这样操作是为了让我们知道出栈的数据是什么。
public int pop(){ if (isEmpty()){ throw new RuntimeException("栈空,无法出栈!"); } //先出栈,后减减 return stack[top--]; }▶ (5)显示栈数据
public void show(){ if (isEmpty()){ System.out.println("栈空,无法显示!"); return; } for (int i = top ; i >= 0; i--){ System.out.printf("stack[%d] = %d\n", i , stack[i]); } }
二、中缀表达式转后缀表达式
1、拆解中缀表达式
首先将中缀表达式拆解成一个一个的字符,存放到集合中,方便后面我们将中缀转后缀时的遍历操作。
首先用split分割操作将原数据分割到数组中存放,然后用增强for循环遍历并同时存放到创建好的stringList集合中。
public static List<String> endList(String s){ String[] s1 = s.split(""); List<String> stringList = new ArrayList<>(); for (String s2 : s1) { stringList.add(s2); } return stringList; }▶ 补充运算符优先级的判断
后面我们转换成后缀表达式时,需要判断运算符的优先级。
public static int Calcu(String s){ char ch = s.charAt(0); if (ch == '-' || ch == '+'){ return 0; } else if (ch == '*' || ch == '/') { return 1; } return -1; }2、中缀转后缀的算法
▶ 初始化两个栈:运算符栈s1和储存中间结果的栈s2
▶ 从左至右扫描中缀表达式
▶ 遇到操作数时,将其压s2
▶ 遇到运算符时, 比较其与s1栈顶运算符的优先级
▷如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈
▷否则,若优先级比栈项运算符的高,也将运算符压入s1
▷否则,将s1栈顶的运算符弹出并压入到s2中 ,再次与s1中新的栈顶运算符相比较
▶ 遇到括号时:
▷ 如果是左括号“(”,则直接压入s1
▷ 如果是右括号“)”,则依次弹出s1栈顶的运算符, 并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
▶ 重复步骤2至5,直到表达式的最右边
▶ 将s1中剩余的运算符依次弹出并压入s2
▶ 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式3、中缀转后缀代码解析
前面的算法说到,首先创建两个栈一个运算符栈和一个中间结果栈,但是根据上面算法的介绍,中间结果栈没有出栈操作,就是数据全部是存入,于是在写代码的时候我们可以将中间结果栈换成集合来存放数据。
首先用增强for循环遍历原数据集合,然后进行判断,如果是数字就放入右方的集合中,如果是运算符就放入左方的符号栈中。
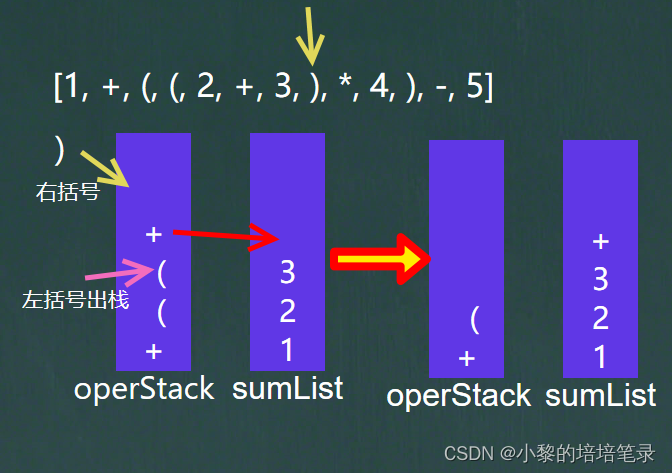
进行运算符判断,如果是左括号“( ” 就直接放入符号栈中,如果是右括号“ )”,就取出符号栈栈顶的符号放入集合中,直到遇到左括号“( ”,停止将栈顶的符号放入集合中,此时将栈顶出栈也就是去掉括号。
然后继续进行遍历放入数据和符号,如果是符号,就与符号栈的栈顶的符号进行比较,要放入运算符的运算级如果小于等于栈顶运算符的运算级,就将栈顶的运算符放入集合中,但下面的图中,运算符为括号,所以不用管,因为括号有单独的判断条件,所以直接放入。
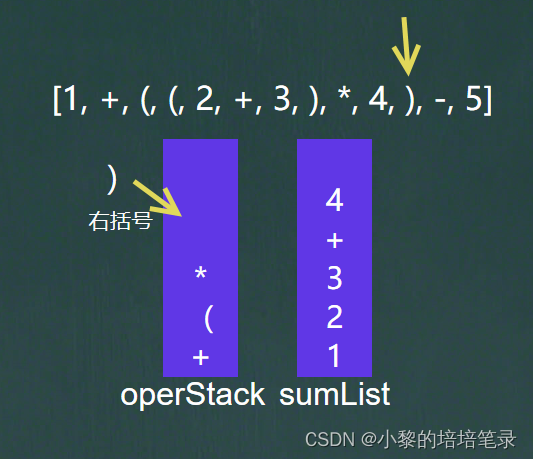
遇到右括号又继续重复前面的操作。
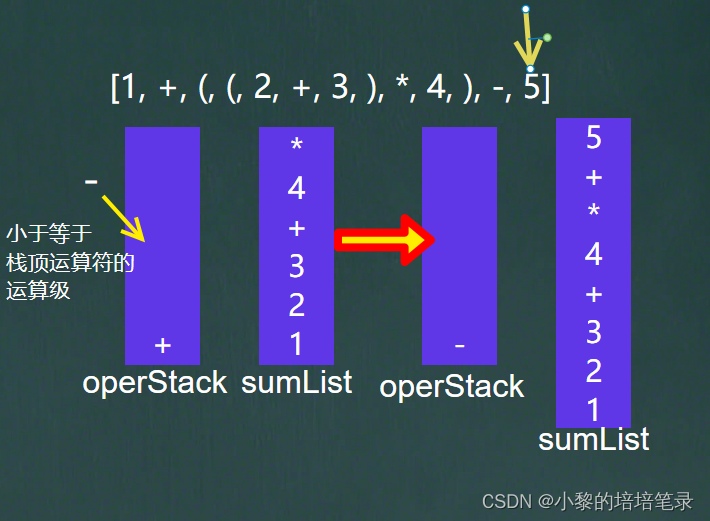
放入运算符的优先级小于等于栈顶运算符的优先级,于是将栈顶的运算符放入集合中,然后放入的运算符继续放入符号栈中。
最后循环结束,将符号栈中的运算符依次放入到集合中。
public static List<String> MiddleToEndExpress(List<String> strings){ //创建栈,存放运算符 Stack<String> operStack = new Stack<>(); //因为这个栈不需要出栈,所以使用集合 List<String> sumList = new ArrayList<>(); for (String s : strings) { //判断是否是数据 if (s.matches("\\d+")){ sumList.add(s);//是数据直接加入 }else if (s.equals("(")){//判断是否是左括号 operStack.push(s);//是,直接放入符号栈 }else if (s.equals(")")){//判断是否是右括号 while (!operStack.peek().equals("(")){//如果栈顶是左括号,退出循环 sumList.add(operStack.pop());//不是左括号,就将栈顶的符号依次放入集合 } //循环结束,表示栈顶是左括号,把左括号去掉,就去掉了一对括号 operStack.pop(); }else {//前面的判断都不是,那就是运算符 //如果符号栈为空,并且运算符小于等于栈顶的运算符优先级 while (operStack.size() != 0 && Calcu(s) <= Calcu(operStack.peek())){ //就将栈顶的运算符放入集合中 sumList.add(operStack.pop()); } //然后将符号放入符号栈中 operStack.push(s); } } //遍历结束,将符号栈剩余的符号依次取出放入集合中 while (operStack.size() != 0){ sumList.add(operStack.pop()); } //最后将集合返回 return sumList; }最后结果为:结果中不能含括号,否则转换错误!
4、对后缀表达式进行计算
前面我们已经将中缀转成后缀表达式了,那么我们只需要直接计算了,首先还是遍历我们的集合(存放后缀表达式的)将数据暂时放入栈中方便我们操作,然后在遍历过程中进行判断,如果是数据就直接放入栈中,如果是运算符就从栈中取出两个数据进行运算,运算结果又放入栈中,直到栈中只存在一个数据时,就是最后的运算结果。文章来源:https://uudwc.com/A/pLJ4g
public static int endCalculator(List<String> stringList){ //创建栈,存放数据 Stack<String> dataStack = new Stack<>(); //循环遍历集合 for (String s : stringList) { //正则表达式判断是否是数据,如果是,就放入栈中 if (s.matches("\\d+")){ dataStack.push(s); }else {//否则就是运算符 //取出两个数据 int num1 = Integer.parseInt(dataStack.pop()); int num2 = Integer.parseInt(dataStack.pop()); //存放运算结果的变量 int res = 0; //判断运算符继续相应的运算 if (s.equals("+")){ res = num1 + num2; }else if (s.equals("-")) { res = num2 - num1; }else if (s.equals("*")) { res = num1 * num2; }else if (s.equals("/")) { res = num2 / num1; }else { throw new RuntimeException("运算符异常!"); } //运算过后将结果又放入栈中 dataStack.push("" + res); } } //最后返回栈中唯一的数据既是结果 return Integer.parseInt(dataStack.pop()); }文章来源地址https://uudwc.com/A/pLJ4g