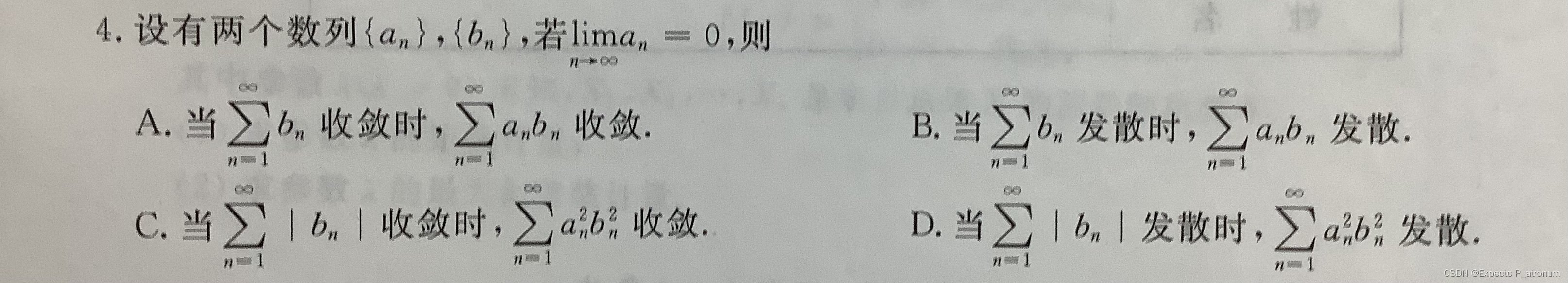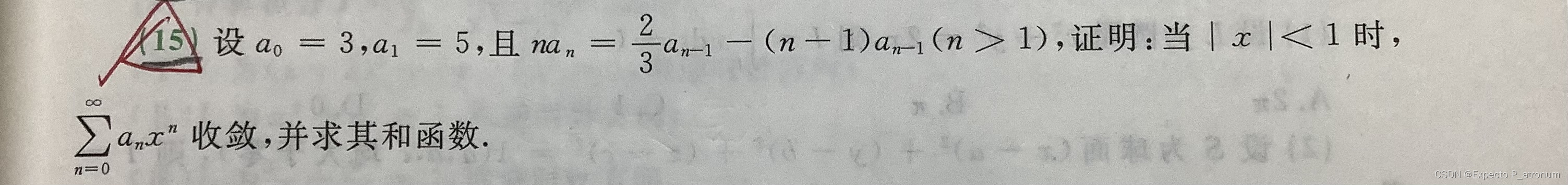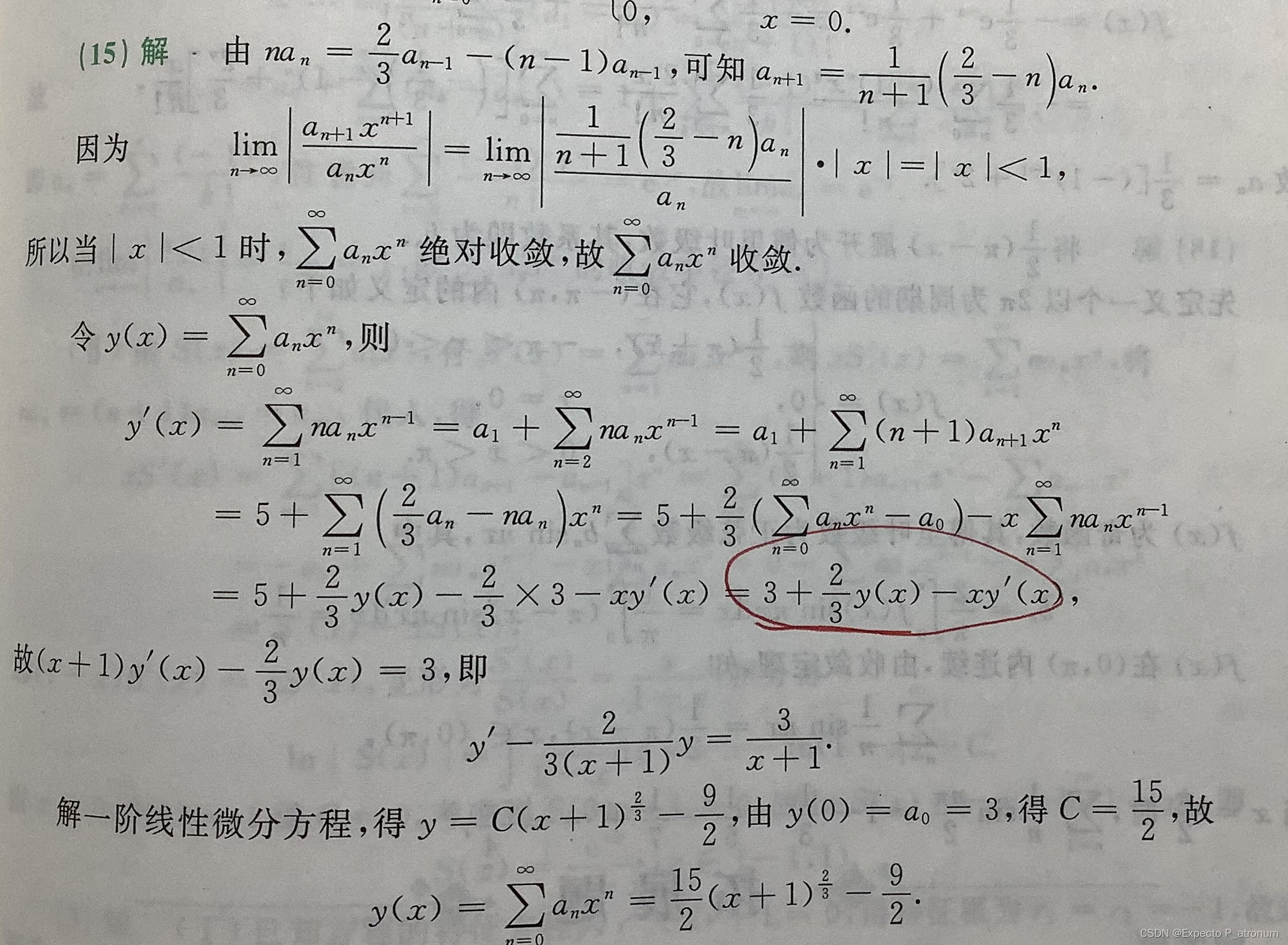一、级数判敛
1、抽象型级数判敛(选择题)
(1)常用结论:
1、绝对收敛 +\- 绝对收敛 = 绝对收敛
2、绝对收敛 +\- 条件收敛 = 条件收敛
3、条件收敛 +\- 条件收敛 = 收敛
4、若收敛,则
收敛,但
不确定
5、发散+发散 = 不确定
(2)?比较审敛法
基本不等式: 、
重要尺度:
绝对收敛可以推
收敛,但
发散无法得知
发散。
对于C、因为
,所以,
必定存在下界M,
,由比较审敛法可以得级数收敛。
2、具体级数判敛
(1)交错级数:?只可能绝对收敛或者发散,用不了莱布尼兹就必定绝对收敛
*莱布尼兹判敛法(充分不必要条件)
在证明时,可以构造函数、利用初等不等式
*绝对收敛:绝对收敛➡️原级数收敛
(2)正项级数:比较审敛法+放缩\常用尺度(大收小收,小散大散),极限审敛法(sinx,cosx,n!),积分判别法(常规难做的),根值判别法(n次方)
(3)等价无穷小之间敛散性相同(利用泰勒公式)tanx,e^x,sinx
(4)前n项和极限存在,级数收敛(充分必要条件)
等价无穷小同敛散
与
是等价无穷小,敛散性相同,所以发散,排除A,D
由莱布尼兹得知,
收敛,所以条件收敛
二、求和函数及展开
1、求和函数
(1)先积后导,先导后积,泰勒公式
(2)解线性微分方程
解线性方程求和函数
2、求和
3、和函数的展开
(1)在x = x0处展开
麦克劳林公式:
(还可以用于求f的n阶导)
(2)直接用泰勒展开
三、求收敛域、收敛区间
(1)收敛域要判断端点敛散性
(2),反向是无法推出来的。也就是说可能存在收敛半径,但极限不存在。
(3)可以适用根值法
(4)非幂级数的收敛域,换元,转换为幂级数
文章来源:https://uudwc.com/A/qR9Ap
四、傅里叶级数
文章来源地址https://uudwc.com/A/qR9Ap