力扣第 365 场周赛虚拟参赛

有序三元组中的最大值 I

class Solution {
public:
    long long maximumTripletValue(vector<int>& nums) {
        vector<long long> num;
        for (auto &item:nums) {
            num.push_back(item*1ll);
        }
        long long z = 0,f = 1000000;
        long long ans = 0;
        long long maxx = num[0],minn = num[0];
        for (int i = 1;i < nums.size();i ++) {
            if (i > 1 ) {
                if (nums[i] > 0) {
                    ans = max(ans,num[i]*z);
                } else {
                    ans = max(ans,num[i]*f);
                }
            }
            z = max(z,maxx-num[i]);
            f = min(f,minn-num[i]);
            minn = min(minn,num[i]);
            maxx = max(maxx,num[i]);
        }
        return ans;
    }
};

有序三元组中的最大值 II

class Solution {
public:
    long long maximumTripletValue(vector<int>& nums) {
        vector<long long> num;
        for (auto &item:nums) {
            num.push_back(item*1ll);
        }
        long long z = 0,f = 1000000;
        long long ans = 0;
        long long maxx = num[0],minn = num[0];
        for (int i = 1;i < nums.size();i ++) {
            if (i > 1 ) {
                if (nums[i] > 0) {
                    ans = max(ans,num[i]*z);
                } else {
                    ans = max(ans,num[i]*f);
                }
            }
            z = max(z,maxx-num[i]);
            f = min(f,minn-num[i]);
            minn = min(minn,num[i]);
            maxx = max(maxx,num[i]);
        }
        return ans;
    }
};

无限数组的最短子数组

• 题意
  
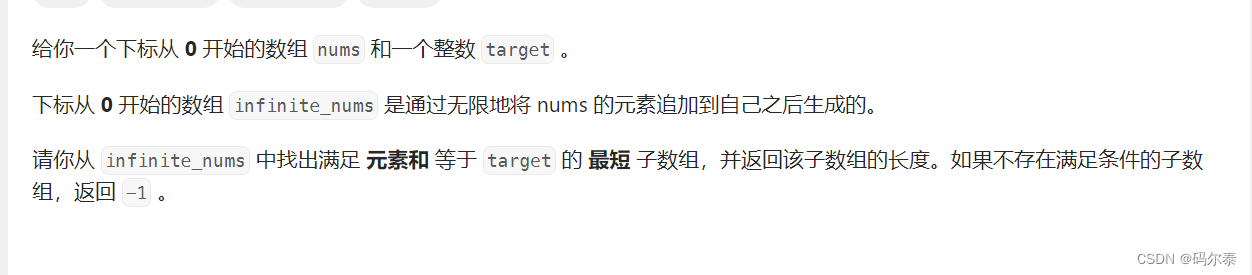
• 思路
  把target/nums_sum 个数加上，剩下的就是拼接一下找最短子数组

class Solution {
public:
    int minSizeSubarray(vector<int> &nums, int target) {
        long long total = accumulate(nums.begin(), nums.end(), 0LL);
        int n = nums.size();
        int ans = INT_MAX;
        int left = 0;
        long long sum = 0;
        for (int right = 0; right < n * 2; right++) {
            sum += nums[right % n];
            while (sum > target % total) {
                sum -= nums[left++ % n];
            }
            if (sum == target % total) {
                ans = min(ans, right - left + 1);
            }
        }
        return ans == INT_MAX ? -1 : ans + target / total * n;
    }
};

有向图访问计数（待补）

• 题意
  
• 思路
  
• 代码

class Solution {
public:
    vector<int> countVisitedNodes(vector<int>& edges) {
        int n = edges.size();
        // e[sn] 表示从 sn 出发的反向边（即原图以 sn 为终点的边）
        vector<int> e[n];
        for (int i = 0; i < n; i++) e[edges[i]].push_back(i);

        // vis 数组用来求环长
        int vis[n];
        memset(vis, 0, sizeof(vis));
        // dis[i] 表示从点 i 走到环上的距离
        int dis[n];
        memset(dis, -1, sizeof(dis));

        vector<int> ans(n);
        // 对每个连通块分别求答案
        for (int S = 0; S < n; S++) if (dis[S] == -1) {
            // 从任意一点出发，都能走到环上，模拟求环长
            int now = S, cnt = 1;
            for (; vis[now] == 0; now = edges[now], cnt++) vis[now] = cnt;
            int loop = cnt - vis[now];
            
            // 从环上每个点开始，在反向边上 bfs，求每个点走到环上的距离
            queue<int> q;
            q.push(now); dis[now] = 0;
            for (int sn = edges[now]; sn != now; sn = edges[sn]) q.push(sn), dis[sn] = 0;
            while (!q.empty()) {
                int sn = q.front(); q.pop();
                // 答案就是环长 + 走到环上的距离
                ans[sn] = dis[sn] + loop;
                for (int fn : e[sn]) if (dis[fn] == -1) {
                    q.push(fn);
                    dis[fn] = dis[sn] + 1;
                }
            }
        }

        return ans;
    }
};

文章来源地址https://uudwc.com/A/rZAOv