[Unity 学习] - 进阶篇 - Mesh基础系列1：生成网格

本文并非原创，只是本人的学习记录，原文是由放牛的星星老师翻译Catlike系列教程
链接: https://mp.weixin.qq.com/s/jIKG2rpNkgVQx2BIWjmYvg

文章目录

[Unity 学习] - 进阶篇 - Mesh基础系列1：生成网格
1 渲染物体
2 创建顶点网格
- - 什么是Gizmos?
3 创建Mesh
4 生成附加顶点数据
- - 法线是怎么计算的？

1 渲染物体

Unity是基于mesh去做渲染的，也就是说你想在Unity里看见东西的话，就必须要使用mesh。
Mesh是什么呢？从概念上讲，mesh是图形硬件用来绘制复杂事物的的框架。它至少包含一个顶点集合（这些顶点是三维空间中的一些坐标，）以及连接这些点的一组三角形（最基本的2D形状）。这些三角形集合在一起就构成任何mesh所代表的表面形状。

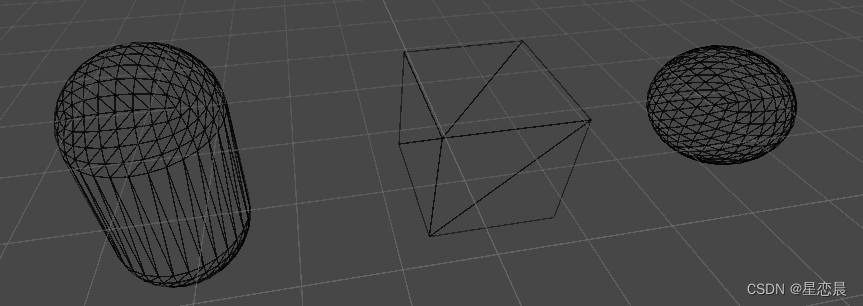
Unity默认的胶囊体，立方体和球体
当我们需要展示一个可见的物体时，物体上面一定需要两个components（mesh filter和mesh renderer）

2 创建顶点网格

创建一个C#脚本Grid

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Grid : MonoBehaviour
{
    public int xSize, ySize;
}

我们现在是做一个mesh，所以需要mesh filter和mesh rendere组件，这里我们可以使用RequireComponent属性，以便Unity自动为我们添加

// RequireCommponent在我们添加这个组件时，会将属性里的其他组件一起添加
[RequireComponent(typeof(MeshFilter), typeof(MeshRenderer))]
public class Grid : MonoBehaviour

创建空的gameobject,添加gird组件，自欧东添加其他两个组件，将gird大小设置为10和5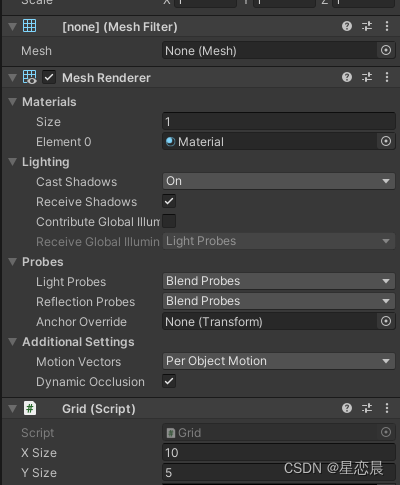
在这里插入图片描述
我们需要一个三维的矢量阵列来存储点，顶点数量取决于gird的大小，由于相邻的四边形共享相同的顶点，所以一个2X4的矩阵，定义3X5顶点即可。

   private Vector3[] vertices;
   ...
   private void Generate()
   { 
       vertices = new Vector3[(xSize + 1) * (ySize + 1)];
  }

我们可以通过定义OnDrawGizeom方法生成一些在sencen场景中显示但是在Game场景中不显示的小球。（这里星星老师少翻译了一部分，这里我们进行一个补充）

什么是Gizmos?

Gizmos是可以在编辑器中使用的视觉提示。默认情况下，它们在场景视图中可见，而在游戏视图中不可见，但您可以通过它们的工具栏进行调整。Gizmos工具类允许您绘制图标、线条和其他一些东西。
Gizmo可以在OnDrawGizmo方法中绘制，该方法由Unity编辑器自动调用。另一种方法是OnDrawGizmosSelected，它仅对选定对象调用。
(百度翻译得已经很清楚了，所以我就直接粘贴了)
这里是代码部分

private void OnDrawGizmos () 
{
		if (vertices == null)
		 {
			return;
		}
		Gizmos.color = Color.black;
		for (int i = 0; i < vertices.Length; i++)
		 {
			Gizmos.DrawSphere(vertices[i], 0.1f);
		}
}

放置gizmos的数组可以在Generate中进行定义

	private void Generate () 
	{
		vertices = new Vector3[(xSize + 1) * (ySize + 1)];
		for (int i = 0, y = 0; y <= ySize; y++) 
		{
			for (int x = 0; x <= xSize; x++, i++)
			 {
				vertices[i] = new Vector3(x, y);
			}
		}
	}

但是我们不明白这样的点放置的位置是否有问题，所以我们可以使用协程的方式将他们放置依次输出出来

private void Awake () 
{
		StartCoroutine(Generate());
}

private IEnumerator Generate () 
{
	WaitForSeconds wait = new WaitForSeconds(0.05f);
	vertices = new Vector3[(xSize + 1) * (ySize + 1)];
	for (int i = 0, y = 0; y <= ySize; y++) 
	{
		for (int x = 0; x <= xSize; x++, i++) 
		{
			vertices[i] = new Vector3(x, y);
			yield return wait;
		}
	}
}

3 创建Mesh

我们已经制动顶点的位置以及顺序是正确的，我们可以处理实际的mesh。除了在我们自己的组件中保存对mesh的引用外，还比较将他分改mesh Filter。当我们处理好顶点后，将其交给给网格处理

	private Mesh mesh;
	private IEnumerator Generate () 
	{
		
		WaitForSeconds wait = new WaitForSeconds(0.05f);
		GetComponent<MeshFilter>().mesh = mesh = new Mesh();
		mesh.name = "Procedural Grid"; // 初始化mesh
		vertices = new Vector3[(xSize + 1) * (ySize + 1)];
		…
		mesh.vertices = vertices; // 交给网格
	}

生成一个三角形面片，triangls是三角形三个顶点分别是那几个点，如果是0,1,2那么就是一条线，vertices记录了所有的顶点，只需要根据index就可以自动找到顶点

		private IEnumerator Generate ()
		{
		…
		int[] triangles = new int[3];
		triangles[0] = 0;
		triangles[1] = 1;
		triangles[2] = xSize + 1;
		mesh.triangles = triangles;
		}

由于三角形面片有正反面，三个点顺时针排列时，才是正面，所以当我们面对z轴的反面时是看不到三角形的，我们可以将，第二点和第三个点反过来就可以看到了triangles[1] = xSize + 1;triangles[2] = 1;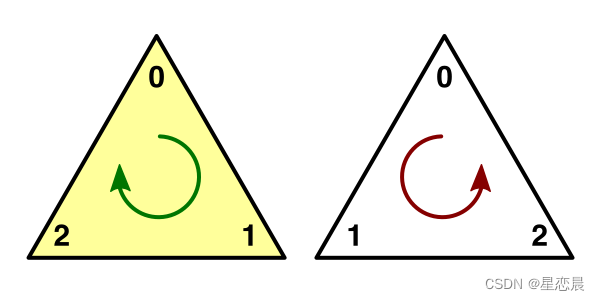
请添加图片描述
接下来我们将第二个三角形面片画出
triangles[3] = 1;
triangles[4] = xSize + 1;
triangles[5] = xSize + 2;
这里有个问题，我们不能用这样一个一个点的方式将三角形画出，所以用循环吧

 // 三角形的那一边可见是由顶点顺序的时钟方向决定的
        // 由于这些三角形共享两个顶点，所以我们可以将其简化为四行代码，只显式地提到每个顶点索引一次。
        int[] triangles = new int[xSize * ySize* 6];
        // 用循环遍历的方式将所有三角形面片都画出来
        // x和vi都是计数器，也可以用一个
        // ti是每个正方形面片的左下角的计数点
        // triangles中的标量是指每个顶点，保存的值是具体哪个顶点
        for(int ti = 0, vi = 0, y = 0; y < ySize; ++y, ++vi)
        {
            for(int x = 0;x < xSize; ++x, ti += 6, ++vi)
            {
                triangles[ti] = vi;
                triangles[ti + 3] = triangles[ti + 2] = vi + 1;
                triangles[ti + 4] = triangles[ti + 1] = vi + xSize + 1;
                triangles[ti + 5] = vi + xSize + 2;
                yield return wait;
            }
        }
        mesh.triangles = triangles;
        yield return wait;

当我们可以合理的将三角形面片生成出来时，就可以将协程干掉了，直接将整个面片画出来

private void Awake () {
		Generate();
	}

	private void Generate () {
		GetComponent<MeshFilter>().mesh = mesh = new Mesh();
		mesh.name = "Procedural Grid";

		vertices = new Vector3[(xSize + 1) * (ySize + 1)];
		for (int i = 0, y = 0; y <= ySize; y++) {
			for (int x = 0; x <= xSize; x++, i++) {
				vertices[i] = new Vector3(x, y);
			}
		}
		mesh.vertices = vertices;

		int[] triangles = new int[xSize * ySize * 6];
		for (int ti = 0, vi = 0, y = 0; y < ySize; y++, vi++) {
			for (int x = 0; x < xSize; x++, ti += 6, vi++) {
				triangles[ti] = vi;
				triangles[ti + 3] = triangles[ti + 2] = vi + 1;
				triangles[ti + 4] = triangles[ti + 1] = vi + xSize + 1;
				triangles[ti + 5] = vi + xSize + 2;
			}
		}
		mesh.triangles = triangles;
	}

4 生成附加顶点数据

我们的需要一个我们自己想要的法线，现在我们所有的三角形的法线都是一样的，但我们不喜欢，我们可以通过提供法线来达到一些“作弊”行为。在现实中，顶点是没有法线的，但三角形有。但是，通过在顶点上附加自定义法线并在它们之间进行三角插值，就可以假装我们有一个平滑的曲面而不是一堆平坦的三角形。这种错觉是能够欺骗普通人的感官的。.
法线是每个顶点单独定义的，所以我们必须填充另外一个向量数组。或者，我们可以要求网格根据其三角形来确定法线本身。这次我们偷下懒。
mesh.RecalculateNormals();//从三角形和顶点重新计算网格的法线。

法线是怎么计算的？

Mesh.RecalculateNormals 计算每个顶点的法线是通过计算哪些三角形与该顶点相连，先确定这些平面三角形的法线，对它们进行平均，最后对结果进行归一化处理。

将纹理适配网格，纹理UV坐标是0-1，所以用顶点位置除以网格尺寸即可，注意这里我们一定要使用浮点才可以

Vector2[] uv = new Vector2[vertices.Length];
for(int i = 0, y = 0; y <= ySize; y++)
{
    for(int x=0;x<=xSize;++x,++i)
    {
        vertices[i] = new Vector3(x, y);
        uv[i] = new Vector2((float)x / xSize, (float)y / ySize);
        tangents[i] = tangent;
    }
}
 mesh.uv = uv;

还有一种简单的方式就是直接使用法线纹理，这个也是我们比较常用的一种方式请添加图片描述
我们需要在网格中添加切线向量来正确的定位它们，表面法线在空间中，是垂直于三角形面片的，但游戏中当然不是这样的，我们的法线方向是由两个切线方向的叉乘所得，所以如果我们希望得到正确的法线，就需要将切线加载到三维空间中。Unity 的着色器执行此计算方式要求我们使用-1.所以我们可以得到一个切线（1,0,0，-1）

    private void Generate()
    { 
       ...
        Vector4[] tangents = new Vector4[vertices.Length];
        Vector4 tangent = new Vector4(1f, 0f, 0f, -1f);
        for(int i = 0, y = 0; y <= ySize; y++)
        {
            for(int x=0;x<=xSize;++x,++i)
            {
                ...
                tangents[i] = tangent;
            }
        }
        ...
     }

在这里插入图片描述
虽然我们看到的这个mesh是凹凸不平的，但事实上，他只是通过数据将一个平面上的法线向量进行了改写。文章来源地址https://uudwc.com/A/zrda